Moore-Penrose inverse of linear operators in Hilbert space

J. M. Mwanzia; M. Kavila; J. M. Khalagai

doi:10.5897/AJMCSR2022.0919

African Journal of
Mathematics and Computer Science Research

Abbreviation: Afr. J. Math. Comput. Sci. Res.
Language: English
ISSN: 2006-9731
DOI: 10.5897/AJMCSR
Start Year: 2008
Published Articles: 262

Full Length Research Paper

Moore-Penrose inverse of linear operators in Hilbert space

J. M. Mwanzia

J. M. Mwanzia
Department of Mathematics and Actuarial Science, Kenyatta University, P. O. Box 43844 - 00100 Nairobi, Kenya.
Search for this author on:
Google Scholar

M. Kavila

M. Kavila
Department of Mathematics and Actuarial Science, Kenyatta University, P. O. Box 43844 - 00100 Nairobi, Kenya.
Search for this author on:
Google Scholar

J. M. Khalagai

J. M. Khalagai
School of Mathematics, University of Nairobi, P. O. Box 30197- 00100 Nairobi, Kenya.
Search for this author on:
Google Scholar

Article Number - 8B1D58169921
Vol.15(2), pp. 5-13 , July 2022
https://doi.org/10.5897/AJMCSR2022.0919

Received: 18 July 2022
Accepted: 25 October 2022
Published: 30 November 2022

Copyright © 2024 Author(s) retain the copyright of this article.
This article is published under the terms of the Creative Commons Attribution License 4.0.

Abstract

In this paper, we investigate properties of 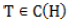with closed range satisfying the operator equations In particular, we investigate the invertibility of 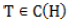with closed range where the Moore-Penrose inverse of T turns out to be the usual inverse of T under some classes of operators. We also deduce the Moore-Penrose inverse of a perturbed linear operator with closed range where such that 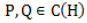has closed ranges and 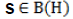satisfying some given conditions. The relation between the ranges and null spaces of these operators is also shown.