ABSTRACT
This research tests the economic convergence hypothesis of 31 inland Chinese provinces over the period from 1952 to 2017. Regression and descriptive analysis methods are adopted to study the economic convergence among these Chinese provinces in terms of GDP growth and per-capita GDP growth. The research results show that GDP growth does not exhibit a tendency of convergence, rejecting the absolute convergence hypothesis among the Chinese provinces. But per-capita GDP growth does suggest convergence, especially after China’s economic reform from 1978 to 2017, supporting the relative convergence hypothesis among the Chinese provinces. Practical and policy implications are provided based on the research results.
Key words: Economic convergence, regression, descriptive analysis, GDP, per-capita GDP, China.
INTRODUCTION AND RESEARCH BACKGROUND
The idea of economic convergence
As directly implied by the assumption of diminishing returns, the classical Solow growth model states that regions or countries that are the same or similar in all of the controlling parameters, such as population growth rates, savings rates, and technical progress rates, should ultimately converge to similar levels of per capita income (Mankiw et al., 1992; Solow, 1956;Sala-i-Martin, 1996). As capital per (efficient) unit of labor must reach to a steady level common to all regions or countries, the general economic convergence will happen irrespective of the initial level of each region, as measured by their starting values of per capita income.
The above economic convergence hypothesis sounds trivial on one hand. Since we assume similar long-run parameters for all regions, naturally expect long-run growth convergence among all regions will be expected. On the other hand, actually the hypothesis is also far from being obvious, since we only assume the same exogenous parameters of economic growth across regions, their initial levels of per capita income (or equivalently, per capita capital stock) are not controlled for. The key point of the economic convergence claim is that, given or assuming similar parameters governing the evolution of the economy for different regions, their different historical conditions or initial states do not matter for where they will arrive in the long-run.
The basic idea of economic convergence can be well explained graphically as shown in Figure 1, which plots the logarithm of per capita income against time, so that a constant growth rate (in the long-run steady state) will appear as a straight line S0S1, where income per (efficient) unit of labor stays precisely at the steady level generated by the steady level of per capita capital, as implied by the Solow growth model. The time path L0L1represents a region or country that starts below the line corresponding to the steady-state per capita level. According to the Solow growth model, this region would Initially grow at a rate higher than that corresponding to the steady-state level. Over time, its growth rate will gradually decelerate to the (lower) steady-state level, or its time path of (log) per capita income will move up asymptotically to the steady S0S1 line as shown. Similarly, a region or country that starts above the line corresponding to the steady state per capita level will follow a growth pattern like U0U1, it would initially experience a lower growth rate but eventually its time path of (log) per capita income will flatten out to the steadyS0S1 line from above. That is, no matter where a region or country started, in the long-run its per capita income will converge to the same steady-state level.
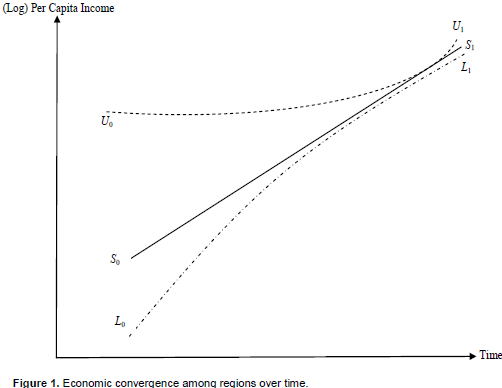
From the above explanations, it is quite clear that economic convergence can be indicated by a (strong) negative relationship between the initial level of per capita income and the subsequent growth rates of per capita income. Largely based on this easily-implementable idea, many studies have been conducted using various statistical analysis methods and data from different regions or countries to validate or reject the classical growth convergence over time.
The economic convergence assertion is important and interesting in both economic theory and practice, which has attracted a great amount of researches to show whether or not there is economic convergence across regions or countries using real data and various statistical methods, especially for developed economies such as the US and European Union (EU) countries where higher quality data are more available over a longer time period. In this regard, it is worth to mention the special contribution made by the ongoing Maddison Project (Maddison 1982, 1991, 2007, see also http://http://www.ggdc.net/maddison/) that compiles data on a larger group of countries over a much longer time period back to the mid-19th century and even earlier.
China’s economic convergence
Just as for other regions or countries in other parts of the world, it is of theoretical and practical interests to investigate the economic convergence among (inland) Chinese provinces regarding certain macroeconomic indicators. Since China started to reform its socialist planned economy to a market-oriented one in late 1978, China has achieved widely-known economic success in the past 40 years, with an average annual growth rate about 8-9%, much higher than the growth rates in developed economies and many other countries. But it has also been noticed in the literature that the income inequality in the Chinese provinces has been increased with possible growth divergence across provinces since 1978 (Cheong and Wu, 2013, 2014; Ho and Li, 2010; Knight, 2014; Lau, 2010; Lyhagen and Rickne, 2014). For example, Ho and Li (2010) investigate the stochastic properties of output per capita across the Chinese provinces for the after-reform period from 1984 to 2003, and observe clear evidence of output divergence across the provinces. Similar evidence is also obtained by Lyhagen and Rickne (2014) for half of Chinese cities using nonlinear trend functions in the vector error correction model (VECM) over a much longer period between 1952 and 2007.
However, there are also many papers in the literature to obtain the evidence of convergence of per capita income (output) across the Chinese provinces (Herrerias and Monfort, 2015; Herrerias and Ordóñez, 2012; Herrerias et al., 2011; Sakamoto and Islam, 2008). For instance, Herrerias et al. (2011) find the evidence of convergence for the per capita GDP across 28 Chinese provinces for the period from 1952 to 2005. Using the panel unit-root method of Phillips and Sul (2007), Herrerias and Ordóñez (2012) investigate the stochastic properties of club convergence in terms of per capita income, labor productivity, and capital intensity for the period from 1952 to 2008. They find a statistically significant club convergence in the Chinese regions over the period under concern. Herrerias and Monfort (2015) also investigate the stochastic properties of convergence across 28 Chinese provinces for the period 1952 from 2008 using the test technique of Phillips and Sul (2007). They observe a significant degree of convergence in capital intensity, labor productivity and total factor productivity (TFP) in the Chinese provinces.
Research objective
Studies are needed to provide more evidence supporting or against economic convergence hypothesis among Chinese provinces. This paper is just to empirically test the economic convergence prediction of the classical Solow growth model in the context of 31 Chinese provinces using more recent data covering a longer period from 1952 to 2017. Having increasingly more international influence, China is very big in terms of land area, population, and economic scale, with 31 inland provinces. Hong Kong, Macao, and Taiwan are the other three special regions of China, which are quite different from the 31 inland provinces historically, economically, and politically, and hence will not be included as in many similar studies. Each of the 31 Chinese provinces is still quite big in land area and population compared to, for example, many EU countries. Thus it is theoretically and methodologically meaningful to study the economic convergence among these Chinese provinces regarding some popular and important economic indicators, which is useful for different provinces to consider different development strategies for future growth. This kind of study is also of a special methodological advantage with no sample selection bias since all inland Chinese provinces are included.
Economic convergence within a group of regions or countries can be generally defined as a decline in the degree of income disparity within the group over time (Simionescu, 2015). Bernard and Durlauf (1995) and Durlauf (1996) distinguish between the two definitions of convergence as output convergence; two regions or countries converge if the logarithm of output per capita for both is the same in the long run, and catching-up convergence; two regions or countries converge between two time points if the difference in the logarithm of output per capita at the earlier time point diminishes in value at the later time point. It is clear that output convergence implies catching-up convergence, but not necessarily vice versa, and that the two definitions can both be generalized to the multivariate cases.
In the economics literature, there is also another pair of widely used concepts: beta-convergence, implying that the poor regions or countries tend to grow faster than rich economies, and sigma-convergence, implying a decrease in income variation between poor and rich economies. It is easy to see that beta-convergence corresponds to output convergence while sigma-convergence matches with catching-up convergence. In both cases, there is a further division between absolute convergence, which implies the same steady-state income or output, and relative convergence, implying that the economies increase at the same rate in steady state.
The empirical methods for examining economic convergence are oriented on a number of different directions, such as the simple correlation and regression methods (Barro, 1991; Baumol, 1986, De Long, 1988; Parente and Prescott, 1993), cross-section augmented Solow regression models (Barro and Sala-i-Martin 1992; Mankiw et al., 1992), the chronological series tests of unit root and co-integration (Evans,1996, 1998; Evans and Karras, 1996a, 1996b; Kutan and Yigit, 2005; Guetat and Serranito, 2007; Siklos, 2010; Lopez and Papell, 2012), and the non-linear time-varying latent factor framework of club convergence (Borsi and Metiu, 2015; Phillips and Sul, 2007; von Lyncker and Thoennessen, 2017).
In terms of practical or empirical applications, there are a great amount of studies in economic convergence, covering different regions or countries in the world over different periods of time. Especially, there have been many studies for regional economic convergence in Europe, largely due to the availability and quality of economic data across European Union (UE) countries over time. For example, Borsi and Metiu (2015) investigate per capita real income convergence between 1970 and 2010 in EU within a non-linear latent factor framework. Quah (1996) shows that in income repartition dynamics, one should take spatial locations and spill overs into account. Sala-i-Martin (1996) assesses beta and sigma-convergence in terms of real GDP per capita in 90 regions of eight countries from Europe. Crespo et al. (2008) measure the beta-convergence in GDP per capita for EU-15 during the period from 1960 to 1998, showing a faster convergence especially for the relatively poorer economies. Cunado and Perez de Garcia (2006) test the real convergence in five countries from East and Central Europe, rejecting the hypothesis of convergence over the period from 1950 to 2003. Cavenaile and Dubois (2011) find conditional beta-convergence for real GDP per capita for the EU-27 countries over the period from 1990 to 2007, with the convergence rates of new members being quite different from the EU-15 countries. Kutan and Yigit (2005) find significant real convergence for the new members of EU over the period from 1993 to 2003. After studying the real GDP and monetary aggregate convergence in CEEC, Brada et al. (2005) conclude that there are limited advantages offered by EMU accession. Kutan and Yigit (2007) show that the economic integration is useful for new member countries only on the long run, while for the founding countries the benefits are immediate. Diaz del Hoyo et al. (2017) show that certain EU countries began to face a “non-convergence trap” long before the euro years by taking a “long view” and reviewing the evidence since the 1960s.
There are also many studies about economic convergence among cities, states or provinces within a big economy like the US (Gerolimetto and Magrini, 2017; Ó’hUallacháin, 2008; Phillips and Sul, 2007; Wang, 2008) and China. A brief literature review about economic convergence among Chinese provinces has already been intentionally conducted in the Introduction with a number of relevant references provided, and hence will not be repeated here again.
When testing the economic convergence hypothesis, the issue of time horizons must be considered. It would be ideal if we could go back one or two centuries in history, but the systematic collection of data for many countries, especially for developing economies, over a so long time period is difficult. In reality, generally we have two choices, the first one is to cover a large number of regions or countries but just over a relatively short period of time, which now is not a problem with the availability of economic data across many regions and countries during the past few decades, as provided by global and regional organizations like the United Nations, World Bank, IMF, OECD, and APEC. The second choice is to cover a relatively small number of countries, largely the more advanced economies like the US and EU countries, but over a long period of time. In this regard, the Maddison Project led by Prof. Angus Maddison has made an important contribution, which has compiled data on a number of countries back to the mid-19th century and even earlier (Maddison 1982, 1991, 2007; Maddison Project webpage athttp://www.ggdc.net/maddison/).It should be noticed that, although the Maddison Project can provide data over the past few decades for many regions and countries, there are only a small number of countries with data stretching back into the nineteenth century.
For example, when William Baumol published one of the earliest studies of long-run economic convergence in 1986, there were only16 countries in Maddison’s database for which per-capita income data were available back to as early as 1870. These countries were, in ascending order of 1870 per capita income, Japan, Finland, Sweden, Norway, Germany, Italy, Austria, France, Canada, Denmark, the United States, the Netherlands, Switzerland, Belgium, the United Kingdom, and Australia, all among the richest countries in the world today. Baumol (1986) plots the 1870 per capita income for these 16 countries on the horizontal axis and their growth rates of per capita income from 1870 to 1979 as measured by the difference in the logs of per capita income over the period on the vertical axis. A strong negative correlation between the 1870 per capita income and the growth rate of that income over the period was observed, which was formally implied by a simple regression (of growth rate on the log of the starting income level) estimated for the 16 countries as follows (Baumol, 1986):
Growth Rate (1870-1979) = 5.25 – 0.75ln(GDPper Work-Hourin 1870), R2 = 0.88 (1)
Hence, the convergence of these 16 countries to one another, starting from very different levels of per capita income in 1870, is undoubtedly verified. It seems that Baumol’s finding quite strongly supports the unconditional convergence hypothesis, but unfortunately it is subject to possible statistical bias in the sense that the 16 countries studied are not selected randomly but just because they are the first group to have historical records in Maddison’s database. Actually, when De Long (1988) adds seven other countries, all with initial per capita income similar to some countries cover in Baumol’ (1986) study, the slope coefficient of the regression of Equation 1is still negative, but the goodness-of-fit is very bad as indicated by the very large residual disturbance terms.
Absolute convergence test
In our study, the same model (1) was used but for all 31 mainland provinces in China, hence the possible sample selection bias issue is eliminated. It was first examines whether GDP (or total income) has any convergence tendency for the 31 Chinese provinces from 1952 to 2017, with data from China Data Online (https://www.china-data-online.com/). Table 1a shows the modelling results, where for each province in the regression, the dependent variable of average GDP growth rate from 1952 to 2017 is formally taken as the difference between the logs of GDP in 2017 and 1952, and the dependent variable of starting GDP level is also taken as the log of GDP in 1952 to be comparable. As can be expected, such kind of absolute convergence among Chinese provinces cannot be supported as the regression has a poor goodness-of-fit (R2 = 0.0414 and p-value = 0.2813 for the slope’s significance test).
It was also checked whether after the 1978 reform, absolute convergence among Chinese provinces can be observed. Table 1b shows the modelling results. The regression output again rejects the convergence hypothesis since the regression has an even poorer goodness-of-fit (R2 = 0.0064 and p-value = 0.6693 for the slope’s significance test).
Relative convergence test
Then the relative convergence hypothesis was tested using GDP per capita data for the 31 Chinese provinces from 1952 to 2017. Table 2a shows the modelling results. The regression outcome confirms the hypothesis with a satisfactory goodness-of-fit (R2 = 0.3705) and a highly significant slope estimate (p-value = 0.0004).
If the relative convergence hypothesis starting from China’s economic reform in 1978 is tested, the conclusion is stronger as the regression has more satisfactory goodness-of-fit (R2 = 0.4837) with a very significant slope estimate (p-value = 0.0000) as reported in Table 2b. This seems to imply that after 1978, there is a stronger tendency than before for Chinese provinces to converge in terms of per capita income.
Another approach
Economic convergence can also be examined without using a modelling approach, but just using appropriate descriptive analysis. For example, Parente and Prescott (1993) study 102 countries from 1960 to 1985. In this study, each country’s per capita real GDP is expressed as a fraction of U.S. per capita GDP for the same year. Then the standard deviation of these values is calculated separately for each year. If the convergence hypothesis holds, these countries should move closer to each other in per capita income levels, and we expect the standard deviation of their relative incomes to fall over time. In Parente and Prescott(1993) study, however, it actually increased by 18.5% over the 26-year period, and the increase was fairly uniform from year to year. Hence the convergence hypothesis could be rejected.
Similar idea in China’s context was used. We first check the absolute convergence issue using the GDP data for China’s 31 provinces from 1952 to 2017. It is observed that the average GDP level among the 31 Chinese provinces increased substantially over the period, the average variation or standard deviation of the 31 provinces’ GDP also increased substantially over the period, but the relative variation in GDP, as measured by the ratio of standard deviation over average, only exhibited a slowly increasing trend, as shown in Figure 2. This implies some kind of stability or convergence among the 31 provinces’ total income (GDP) levels.
When we do the same using the per capita GDP data for China’s 31 provinces from 1952 to 2017, another picture was find (Figure 3) showing the relative convergence. It is observed that, as in the above GDP case, the average per capita income (GDP) level among the 31 Chinese provinces increased substantially over the period, and the average variation or standard deviation of the 31 provinces’ per capita GDP also increased substantially over the period, but the relative variation in per capita GDP, as measured by the ratio of standard deviation over average, exhibited a somewhat clear decreasing trend, especially after 1978 when China started its economic reform. This implies again a kind of stability or convergence among the 31 provinces’ per capita income (GDP) levels.
For each year from 1952 to 2017, when we consider the ratio of each province’s GDP over the GDP of Beijing, and the ratio of each province’s per capita GDP over the per capita GDP of Beijing (Figures 4 and 5), we find quite similar results as above, which further confirms certain kind of economic convergence among China’s 31 provinces in the past several decades.
This research empirically tests the economic convergence prediction of the classical Solow growth model in the context of 31 Chinese provinces. Simple regression and descriptive analysis methods are adopted to study the economic convergence among these Chinese provinces in terms of GDP growth and per-capita GDP growth. Our regression results show that, GDP growth does not exhibit a strong tendency of convergence, rejecting the absolute convergence hypothesis among the Chinese provinces, for the whole time period from 1952 to 2017 and the reform period from 1978 to 2017 as well. However, per-capita GDP growth does suggest convergence, especially after China’s economic reform from 1978 to 2017, supporting the relative convergence hypothesis among the Chinese provinces.
Descriptive analysis further confirms the results. In terms of standard deviations over average and also relative to Beijing’s, GDP growth does not exhibit convergence, while per-capita GDP growth does suggest convergence, especially after China’s economic reform, again rejecting the absolute convergence hypothesis and supporting the relative convergence hypothesis among the Chinese provinces.
Our research results have meaningful implications. Rejection of the absolute convergence hypothesis shows that, due to differences in, e.g., resources, technologies and initial conditions, GDP growth in different Chinese provinces still quite differs. Less developed provinces should work harder to catch up with the more developed provinces, which may help achieve regional economic balance in the long run. Supporting of the relative convergence hypothesis suggests that, although differs a lot in GDP growth or economic scale, different Chinese provinces tend to converge in per-capita GDP growth or average income, especially after China’s economic reform since 1978. This is an encouraging trend, which shows the great economic success in China, not only in GDP growth or efficiency, but more importantly in average income growth of equality.
It may be argued that our research results are not robust and may change by taking different approaches, which however should be the case. From the brief review in this paper’s Introduction part, different studies do get different results about economic convergence among Chinese provinces. If much more studies can provide similar results, then the results will reasonably become more reliable. Our study is just to provide further evidence in this regard, hopefully contributing to the accumulation of the relevant knowledge. In the future, more studies about economic convergence among Chinese provinces should be conducted using different methods and economic indicators (including, for example, consumer price index, total capital investment, and consumption-income ratio) over different and possibly longer time periods, so as to get more comprehensive and possibly more consistent and reliable results.
This research was supported by a research grant (R201832) from United International College, Beijing Normal University-Hong Kong Baptist University.
The author has not declared any conflict of interests.
REFERENCES
|
Barro RJ (1991). Economic growth in a cross section of countries. The Quarterly Journal of Economics 106(2):407-443.
Crossref
|
|
|
|
Barro R J, Sala-i-Martin XX (1992). Convergence. Journal of Political Economy 100(2):223-251.
Crossref
|
|
|
|
|
Baumol WJ (1986). Productivity growth, convergence, and welfare: What the long-run data show. The American Economic Review 76(5):1072-1085.
|
|
|
|
|
Bernard AB, Durlauf SN (1995). Convergence in international output. Journal of Applied Econometrics 10(2):97-108.
Crossref
|
|
|
|
|
Borsi MT, Metiu N (2015). The evolution of economic convergence in the European Union. Empirical Economics 48(2):657-681.
Crossref
|
|
|
|
|
Brada JC, KutanAM, Zhou S (2005). Real and monetary convergence between the European Union's core and recent member countries: A rolling cointegration approach. Journal of Banking and Finance 29(1):249-270.
Crossref
|
|
|
|
|
Cavenaile L, Dubois D (2011). An empirical analysis of income convergence in the European Union. Applied Economics Letters 18(17):1705-1708.
Crossref
|
|
|
|
|
Cheong TS, Wu Y (2013).Regional disparity, transitional dynamics and convergence in China. Journal of Asian Economics 29:1-14.
Crossref
|
|
|
|
|
Cheong TS, Wu Y (2014).The impacts of structural transformation and industrial upgrading on regional inequality in China. China Economic Review 31:339-350.
Crossref
|
|
|
|
|
Crespo CJ, Ritzberger-Grunwald D,Silgoner MA (2008).Growth, convergence and EU membership. Applied Economics 40(5):643-656.
Crossref
|
|
|
|
|
Cunado J, Perez de Gracia F (2006). Real convergence in some Central and Eastern European countries.Applied Economics 38(20):2433-2441.
Crossref
|
|
|
|
|
DeLong JB (1988). Productivity growth, convergence, and welfare: comment. American Economic Review 78(5):1138-1154.
|
|
|
|
|
Diaz del Hoyo JL, Dorrucci E, Heinz FF, Muzikarova S (2017). Real convergence in the euro area: a long-term perspective. ECB Occasional Paper 203(December).
|
|
|
|
|
Durlauf SN (1996). On the convergence and divergence of growth rates. The Economic Journal 106(437):1016-1018.
Crossref
|
|
|
|
|
Evans P (1996). Using cross-country variances to evaluate growth theories. Journal of Economic Dynamics and Control 20(6-7):1027-1049.
Crossref
|
|
|
|
|
Evans P (1998). Using panel data to evaluate growth theories. International Economic Review 39(2):295-306.
Crossref
|
|
|
|
|
Evans P, Karras G (1996a). Convergence revisited. Journal of Monetary Economics 37(2):249-265.
Crossref
|
|
|
|
|
Evans P, Karras G (1996b). Do economies converge? Evidence from a panel of US states. The Review of Economics and Statistics 78(3):384-388.
Crossref
|
|
|
|
|
Gerolimetto M, Magrini S (2017). A novel look at long-run convergence dynamics in the United States. International Regional Science Review 40(3):241.
Crossref
|
|
|
|
|
Guetat I, Serranito F (2007). Income convergence within the MENA countries: A panel unit root approach. The Quarterly Review of Economics and Finance 46(5):685-706.
Crossref
|
|
|
|
|
Herrerias MJ, Monfort JO (2015). Testing stochastic convergence across Chinese provinces, 1952-2008. Regional Studies 49(4):485-501.
Crossref
|
|
|
|
|
Herrerias MJ, Ordóñez J (2012). New evidence on the role of regional clusters and convergence in China (1952-2008). China Economic Review 23(4):1120-1133.
Crossref
|
|
|
|
|
Herrerias MJ, Orts V, Tortosaâ€Ausina E (2011). Weighted convergence and regional clusters across China. Papers in Regional Science 90(4):703-734.
Crossref
|
|
|
|
|
Ho CY, Li D (2010).Spatial dependence and divergence across Chinese cities. Review of Development Economics 14(2):386-403.
Crossref
|
|
|
|
|
Knight J (2014). Inequality in China: An overview. The World Bank Research Observer 29(1):1-19.
Crossref
|
|
|
|
|
Kutan AM,Yigit TM (2005). Real and nominal stochastic convergence: Are the new EU members ready to join the Euro zone? Journal of Comparative Economics 33(2):387-400.
Crossref
|
|
|
|
|
Kutan AM,Yigit TM (2007). European integration, productivity growth and real convergence. European Economic Review 51(6):1370-1395.
Crossref
|
|
|
|
|
Lau CKM (2010). New evidence about regional income divergence in China. China Economic Review 21(2):293-309.
Crossref
|
|
|
|
|
Lopez C, Papell DH (2012). Convergence of euro area inflation rates. Journal of International Money and Finance 31(6):1440-1458.
Crossref
|
|
|
|
|
Lyhagen J, Rickne J (2014). Income inequality between Chinese regions: Newfound harmony or continued discord? Empirical Economics 47(1):93-110.
Crossref
|
|
|
|
|
Maddison A (1982). Phases of Capitalist Development. New York: Oxford University Press.
|
|
|
|
|
Maddison A (1991). Dynamic Forces in Capitalist Development. New York: Oxford University Press.
|
|
|
|
|
Maddison A (2007). Contours of the World Economy 1-2030 AD: Essays in Macroeconomic History. New York: Oxford University Press.
|
|
|
|
|
Mankiw NG, Romer D, Weil DN (1992). A contribution to the empirics of economic growth. The Quarterly Journal of Economics 107(2):407-437.
Crossref
|
|
|
|
|
Ó'hUallacháin B (2008). Regional growth transition clubs in the United States. Papers in Regional Science 87(1):33-53.
Crossref
|
|
|
|
|
Phillips PCB, Sul D (2007). Transition modeling and econometric convergence tests. Econometrica 75 (6):1771-1855.
Crossref
|
|
|
|
|
Quah DT (1996). Empirics for economic growth and convergence. European Economic Review 40(6):1353-1375.
Crossref
|
|
|
|
|
Sakamoto H, Islam N (2008). Convergence across Chinese provinces: An analysis using Markov transition matrix. China Economic Review 19(1):66-79.
Crossref
|
|
|
|
|
Sala-i-Martin XX (1996). Regional cohesion: evidence and theories of regional growth and convergence. European Economic Review 40(6):1325-1352.
Crossref
|
|
|
|
|
Sala-i-Martin XX (1996). The classical approach to convergence analysis. Economic Journal - Royal Economic Society 106(437):1019-1036.
Crossref
|
|
|
|
|
Siklos PL (2010). Meeting Maastricht: Nominal convergence of the new member states toward EMU. Economic Modelling 27(2):507-515.
Crossref
|
|
|
|
|
Simionescu M (2015). About regional convergence clubs in the European Union. Zbornikradova Ekonomskogfakulteta u Rijeci 33(1):67-80.
|
|
|
|
|
Parente SL, Prescott EC (1993).Changes in the Wealth of Nations. Quarterly Review. Federal Reserve Bank of Minneapolis 17(2):3-16.
Crossref
|
|
|
|
|
Solow RM (1956). A contribution to the theory of economic growth. Quarterly Journal of Economics 70(February):65-94.
Crossref
|
|
|
|
|
vonLyncker K, Thoennessen R (2017). Regional club convergence in the EU: Evidence from a panel data analysis. Empirical Economics 52:525-553.
Crossref
|
|
|
|
|
Wang Z (2008). The convergence of health care expenditure in the US states. Health Economics 18(1):55-70.
Crossref
|
|