ABSTRACT
The Blaney-Morin-Nigeria (BMN) model was developed for the estimation of reference evapotranspiration (ETo) in Nigeria using commonly available meteorological parameters. In the development of the model, there were some perceived shortcomings which are believed to affect the reliability of ETo estimation, particularly in some specific locations in Nigeria, due to varying environmental factors. This study re-examined the model by using the non linear regression model based on Levenberg-Marquardt Algorithm (Excel Solver) to minimize the error space and generate new model constants specific for Enugu. A 25-year (1989 to 2014) monthly record of climatic variables (Solar radiation, Temperature, Relative Humidity and Wind speed) for Enugu were collected from the Nigeria Meteorological Agency (NIMET), Abuja in Nigeria and used. The newly generated model constants, H and m, were 392.2 and 1.19, respectively. Reference evapotranspiration for Enugu [ET 0(nBMN)] was thereafter estimated using the optimized BMN model and compared with that calculated using the FAO56-PM model [ET 0(FA056-PM)]. The optimized model showed a more accurate estimation of ET for Enugu as indicated by the higher correlation coefficient of 0.82 compared to 0.76 for the original BMN, lower mean absolute error (MAE) of 0.133 compared to 0.42 and root mean square (RMSE) of 0.3641 compared to 0.44. The X2 of 0.135 obtained using the optimized model was also low showing that the new model gives a better estimation of ET for Enugu, Nigeria.
Key words: Evapotranspiration, Blaney-Morin-Nigeria model, FAO56-PM model, Levenberg-Marquardt Algorithm, Enugu, Nigeria.
Water availability is one of the important factors considered in Agriculture. Water is provided to crop through natural precipitation and subsurface moisture. In many areas of the world where rainfall is insufficient to meet the crop water demand, irrigation system is often used to offset the water deficit. Water is lost from crops through evaporation and transpiration. Evaporation is the process of liquid water conversion to water vapour and removal from the evaporating surface. Transpiration includes the vaporization of liquid water contained in plant tissues and the water removal to the atmosphere. Evapotranspiration (ET), which is the combination of evaporation and transpiration, is also known as the consumptive use or actual evapotranspiration (Allen et al., 1998).
The rate of ET is determined using different approaches. As indicated by Ilesanmi et al. (2012), these approaches may be broadly classified into direct and indirect measurement. The direct measurement include the use of lysimeters (Ayoade, 1988, 1988a; Meissner et al., 2010) and atmometers (Diop et al., 2015), energy balance/budget approach (Adeboye et al., 2009; Farahani, et al., 2007), the soil water budget method (Phene et al., 1990; Evett and Parkin, 2005; Farahani et al., 2007), the use of pan evaporimeters (Ayoade, 1988, 1988a; Howell et al., 1991; Young et al., 1996; Yang et al., 2000; Gavilan et al., 2007), satellite remote sensing (Bastiaanssen et al., 2005; Tang et al., 2009) and the Eddy-Covariance method (Shuttleworth, 1993, 2007). Direct measurement of evapotranspration is usually not feasible in many situations because it is expensive and relatively time consuming (Igbadum et al., 2006). The indirect measurement involves the use of empirical models developed to estimate ET using meteorological data. These models range from simple expressions which relate ET to temperature and/or radiation to models having extensive data requirement. The models may be classified into three: Temperature-based models (Thornthwaite, Blaney-Cridle, Blaney-Morin and McCloud models); radiation-based models (Turc, Hargreaves, Hargreaves-Samani, Priestly-Taylor and the Makkink Formula) and a combination approach based on original Penman model which consists of radiation and aerodynamic part (Jacobs and Satti, 2001; Alexandris et al., 2008, Ilesanmi et al., 2012). Penman’s model has been modified over the years because it produces good results when applied over different climatic regions (Allen et al., 1998). One of its modification is the FAO56 Penman-Monteith model (FAO56-PM) which has been adjudged to be the best estimator of Reference Evapotranspiration (ETo) and has been recommended as the model to be used for the estimation of ETo from meteorological data (Allen et al., 1998; Alexandris et al., 2008) if all meteorological data is available.
In Nigeria, as in most developing countries, the meteorological data needed for the calculation of ETo using models such as the FAO56-PM are most of the time not readily available (Adeboye et al., 2009). For Nigeria, therefore, a temperature based model - the Blaney-Morin-Nigeria (BMN) - developed by Duru (1984) has been adjudged to be the best for the Nigerian condition by the Nigerian Institute of Agricultural Engineers (NIAE). In the development of this model, there are some perceived shortcomings which are believed to affect its reliability for ET estimation in Nigeria. These shortcomings have been exhaustively discussed by Idike and Aneke (2002), Idike (2005) and Ilesanmi et al. (2012) among other researchers. This study was therefore carried out to generate a modified version of the BMN model that is specific for Enugu, Nigeria.
Study area
Enugu, which is the capital city of Enugu State, in Nigeria, was used for the study (Figure 1). It is lies within Latitude: 6°26′33″ N, Longitude: 7°30′07″ E with an elevation of 227 m above sea level. Located in the tropical rain forest zone of Nigeria, Enugu’s vegetation is derived savannah. The area has a humid climate with a mean daily temperature of 26.7°C, a mean relative humidity of 72% and an average annual rainfall of 2000 mm. The humidity is highest between March and November when it attains a mean value of over 80%. As in the rest of West Africa, there are two major seasons: the rainy season and dry season. The rainy season lasts from April to November while the dry season lasts from January to April. In between, is the Harmattan season which is characterized by very low relative humidity and a very dry and dusty wind. Like the rest of Nigeria, Enugu is hot all year round (Wikipedia, 2016).
Data source
Monthly weather data for Enugu covering a period of 25 years (1989 - 2014) was collected from the Nigeria Meteorological Agency (NIMET), Abuja. The data includes solar radiation, maximum and minimum temperature, relative humidity and wind speed.
Model optimization
The Blaney-Morin-Nigeria (BMN) model developed for the estimation of reference evapotranspiration in Nigeria by Duru (1984) formed the basis for the optimization exercise. The model is given by:
Model accuracy
Four criterion were used to test the accuracy of the new model constants for estimating ET. They are:
1. The mean absolute error (MAE): This gives the mean difference between the observed and predicted values.
In Equations 2 to 5, observed or experimental data refer to ET
o values calculated using the FAO56-PM model while predicted refers to values determined using the optimized BMN model. According to Duru (1984), the closer to zero the values of MAE, RMSE, and
 2
2, the better performed the respective model, whereas the closer to unity (1.0) the value of
r, the better the model. Also, according to Duru (1984), “from a design and safety standpoint, a model that over predicts should be preferred to one that under predicts and the better model is one that over predicts to a lesser degree” (Ilesanmi et al., 2012).
Weather data
Estimated model constants
A comparison of the old (Duru, 1984) and the newly developed model constants are shown in Table 2. From the table, it is seen that while the model constants estimated by Duru for H and m were 520 and 1.33 respectively, the newly estimated values for the constants using the Levenberg-Marquardt Algorithm were 392.2 and 1.19, respectively. These values are lower than those of Duru (1984). The lower values agree with the result obtained by Ilesanmi et al. (2012) who used similar method to recalibrate the BMN model for estimating ETo for some other Nigerian locations.
The optimized BMN model for Enugu is, therefore, of the form:
Comparison between FAO56-PM and New BMN model's
The plots of the predicted and actual ET for some typical years (2006 and 2014) are shown in Figure 3. The same pattern, as observed for the mean values over the study period, is also exhibited for the shown typical years.
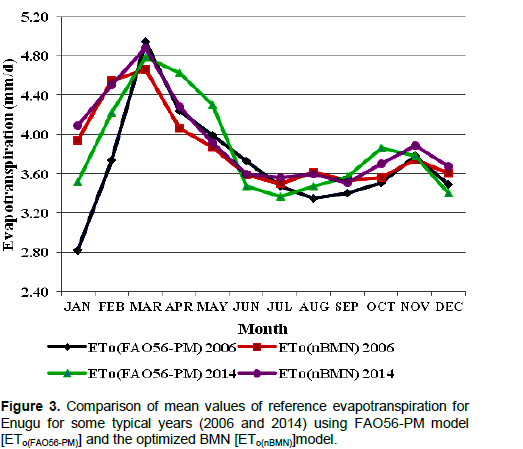
The mean absolute error (MAE), root mean square (RMSE), Chi square (
 2
2) and correlation coefficient (
r) for the optimized BMN model are shown in Table 3. Also shown in the table are similar values as obtained by Duru (1984) using the original BMN model. The MAE and RMSE of 0.133 and 0.3641, respectively, are lower than those obtained with Duru’s model which was 0.42 and 0.44, respectively. The correlation coefficient of 0.82 was higher than that of Duru’s model which was 0.76. As stated earlier, the closer to zero the values of MAE, RMSE, and
 2
2, the better the model, whereas the closer to unity (1.0) the value of
r, the better. The estimated MAE and RMSE are lower than that of Duru showing that the modified model gives a better estimate of ET for Enugu, Nigeria. Although Duru (1984) did not compute the

value for his model, the value for the developed model was 0.135 which is relatively low indicating a good prediction. Also the correlation coefficient of 0.82 shows a better prediction when compared with Duru’s model with an
r value of 0.76.
The fact that optimized BMN gave a better estimation of ETo is to be expected. Among the perceived shortcomings in the development of Duru’s model was the fact that the relevant meteorological data used in developing the model was obtained from only one location (Zaria, Northern Nigeria); yet the model was developed for use throughout Nigeria and possibly the West African sub-region (Idike, 2005). Manual iteration was also used during its development and this is prone to errors (Ilesanmi et al., 2012) and hence likely to lead to lesser reliability.
Compared to the correlation coefficient (r) values computed by Duru (1984) for other Nigerian locations, the correlation coefficient of 0.82 obtained for Enugu using the optimized BMN model was the highest. For example the highest correlation coefficient recorded by Duru was 0.80 for Lagos while the lowest was 0.62 for Gombe in Northern Nigeria. Also the MAE of 0.133 and RMSE of 0.3641 obtained with the optimized BMN model were lower that similar values determined for other Nigerian location by Duru. The lowest MAE and RMSE recorded by Duru in his model were 0.40 and 0.40, respectively (Duru, 1984). The values were obtained for Akure and Lagos, respectively.
This study outlined the effect of the corrections done to the old BMN model for the estimation of evapotranspiration. From the results obtained during the data analysis, the newly developed location specific BMN model proved to be a more accurate estimator of ETo when applied to Enugu location. This is because this work utilized a standard statistical procedure in its calibration rather than the manual iteration method previously employed by Duru (1984) in the development of the original model. The overall result indicates that the Blaney-Morin-Nigeria model is location specific and that the newly generated models fared better and has improved performances than the BMN for the location considered for this study. For further study, other models such as Priestly-Taylor Model, Hargreaves-Samani Model could also be used to further re-examine the BMN model for this and other study areas. Also actual field data could be used to test the accuracy of the new model instead of the data generated using FAO56-PM model.
There is absolutely no conflict of interests known to the author with regards to this manuscript.
REFERENCES
|
Adeboye OB, Osunbitan JA, Adekalu KO, Okunade DA (2009). Evaluation of FAO-56 Penman-Monteith and temperature based models in estimating reference evapotranspiration using complete and limited data, application to Nigeria. Agric. Eng. Int. CIGR J.
|
|
|
|
Allen RG, Pereira LS, Raes D, Smith M (1998). Crop evapotranspiration - Guidelines for computing crop water requirements - FAO Irrigation and drainage paper 56. FAO - Food and Agriculture Organization of the United Nations Rome, 1998.
|
|
|
|
|
Alexandris S, Stricevic R, Petkovic S (2008). Comparative analysis of reference evapotranspiration from the surface of rainfed grass in central Serbia, calculated by six empirical methods against the Penman-Monteith formula. Eur. Water 21(22):17-28.
|
|
|
|
|
Ayoade JO (1988). Introduction to Climatology for the Tropics. Spectrum Books Ltd, Ibadan.
|
|
|
|
|
Ayoade OA (1988a). Tropical hydrology and water resources. Macmillan publishing, London. pp. 10-25.
|
|
|
|
|
Bastiaanssen WGM, Noordman EJM, Pelgrum H, Davids G, Thoreson BP, Allen RG (2005). SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 131(1):85-93.
Crossref
|
|
|
|
|
Duru JO (1984). Blaney-Morin-Nigeria evapotranspiration model. J. Hydrol. 70:71-83.
Crossref
|
|
|
|
|
Evett SR, Parkin GW (2005). Advances in soil water content sensing: the continuing maturation of technology. Vadose zone J. 4(4):986-991.
Crossref
|
|
|
|
|
Farahani HJ, Howell TA, Shuttleworth WJ, Bausch WC (2007). Evapotranspiration: progress in measurement and modeling in agriculture. Trans. ASABE 50(5):1627-1638.
Crossref
|
|
|
|
|
Gavilan P, Berengena J, Allen RG (2007). Measuring versus estimating net radiation and soil heat flux: Impact of Penman-Monteith reference ET estimates in semiarid regions. Agric. Water Manag. 89(3):275-286.
Crossref
|
|
|
|
|
Howell TA, Schneider AD, Jensen ME (1991). History of lysimeter design and use for evapotranspiration measurements. In: Allen RG, Howell TA, Pruitt WO, Walter IA, Jensen ME (Eds.). Proceedings of ASCE Int'l Symposium on Lysimetry: Lysimeter for Evapotranspiration and Environmental Measurement. ASCE New York.
|
|
|
|
|
Igbadum H, Mahoo H, Tarimo A, Salim B (2006) Crop water productivity of an irrigated maize crop in Mkoji sub-catchment of Great Ruaha River Basin, Tanzania. Agric. Water Manage. 85:141-150.
Crossref
|
|
|
|
|
Idike FI, Aneke DG (2002). Evaluation, analysis and modification of the Blaney-Morin-Nigeria (BMN) evapotranspiration model. Niger. J. Technol. 21(1):18-29.
|
|
|
|
|
Idike FI (2005). Blaney-Morin-Nigeria (BMN) evapotranspiration model (A technical Note). Niger. J. Technol. 24(2):101-104.
|
|
|
|
|
Ilesanmi OA, Oguntade PG, Olufayo AA (2012). Re-examination of the BMN model for estimating evapotranspiration. Int. J. Agric. For. 2(6):268-272.
Crossref
|
|
|
|
|
Jacobs JM, Satti SR (2001). Evaluation of reference evapotranspiration. Methodologies and AFSIRS Crop Water Use Simulation Model (Final Report). Department of Civil and Coastal Engineering, University of Florida, Gainesville, Florida.
|
|
|
|
|
Levenberg K (1944). A method for the solution of certain problems in the least squares. Q. Appl. Math. 2:164-168.
|
|
|
|
|
Marquardt DW (1963). An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 11(2):431-441.
Crossref
|
|
|
|
|
Meissner R, Rupp H, Seeger J, Ollesch G, Gee GW (2010). A comparison of water flux measurements: passive wick samplers versus drainage lysimeters. Eur. J. Soil Sci. 61:609-621.
Crossref
|
|
|
|
|
Phene CJ, Reginato RJ, Itier B, Tanner BR (1990). Sensing irrigation needs. In: Hoffman GJ, Howell TA, Solomon KH (Eds.). Management of Farm Irrigation Systems: 207-261. St. Joseph, Mich. ASAE.
|
|
|
|
|
Shuttleworth WJ (1993). Evaporation. In: Maidment D (Ed.). Handbook of Hydrology. New York. McGraw-Hill.
|
|
|
|
|
Shuttleworth WJ (2007). Putting the "vap" into evaporation. Hydrol. Earth Syst. Sci. 11(1):210-244.
Crossref
|
|
|
|
|
Tang Q, Peterson S, Cuenca RH, Hagimoto Y, Lettenmaier DP (2009). Satellite-based near-real-time estimation of irrigated crop water consumption, J. Geophys. Res. 114:D05114.
Crossref
|
|
|
|
|
Wikipedia (2016). Enugu. https://en.wikipedia.org/wiki/Enugu#Climate. Retrieved on 28th March, 2016.
|
|
|
|
|
Yang J, Li B, Liu S (2000). A large weighing lysimeter for evapotranspiratiion and soil water and ground water exchange studies. Hydrol. Process. 14(10):1887-1897.
Crossref
|
|
|
|
|
Young MH, Wierenga PJ, Mancino CF (1996). Large weighing lysimeters for water use and deep percolation studies. Soil Sci. 161(8):491-501.
Crossref
|
|