The pressurized irrigation system implies an application of different pipelines in the irrigation fields. These pipelines have a long life and low maintenance costs when properly installed. They are essentially leak proof and water supply to the field plots are controlled precisely through the water distribution system. Since, this system operate under pressure, they can be applied in uphill or downhill sections, permitting delivery of irrigation water to areas not accessible to open channels or other distribution systems. Their initial cost is high as compared to lined channels, but is more economical under many field conditions and for long term use.

There are different types of pressurized irrigation methods, such as sprinkler, drip, and micro-sprinkler. These methods become increasingly popular due to their higher water application and distribution efficiencies. The sprinkler irrigation technology was considered to be the most efficient one prior to the development of trickle/drip irrigation technology. The drip irrigation is now one of the fastest growing technologies in modern agriculture and has proved to be the most efficient one. It has gained worldwide popularity, particularly in water scarce areas, undulating hill areas, and saline areas.

The modernization of irrigation distribution systems is mainly based on replacing the open channels by pressurized systems, which include the application of pipeline systems. The soluble fertilizers, herbicides, and fungicides can be applied through irrigation water economically and with little extra equipment. The pressurized systems guarantee higher and better distribution efficiency by eliminating the seepage and evaporation losses that occur in open channel systems and allow better control on the volume withdrawn by the farmers. The design of any water conveyance system for this system involves the selection of different sizes of pipes, materials, and equipment for utmost economy. The Indian farmers depend mainly on the earthen channels, from which much amount of water gets lost by evaporation and seepage, that is, of the order of 10 to 40% of the total water supply (Kumar, 1976).

There are different types of pipe materials which are used in water distribution system. The pipelines are normally design to deliver fluid at the required head and flow rate in a cost effective manner. The optimal selection, design, and managing of irrigation systems at farm level is an important factor for rational use of water, economic development of the agriculture, and its environmental sustainability. Some of the acceptable materials for this research work are commercial pipes, such as poly vinyl chloride (PVC), galvanized iron, and reinforced cement concrete (RCC) pipe. The increase in conduit diameter leads to increase in annual capital costs and increase in operating costs. The selection of an optimum conduit diameter for a particular fluid flow will therefore be a vital economic decision. When water is to be pumped at a known rate through a long pipeline, the designer may select a small diameter pipe to save the cost but this normally results in high pumping costs due to high friction loss in small size pipes.

In this system of water distribution, there are many factors which affect the flow of water in the pipes, such as, Reynolds number which is inversely proportional to friction factor (governed by roughness coefficient) for the pipe material. Koo and Blasius correlation factors are governed by laminar flow (Re < 2000) and turbulent flow (Re > 4000). The average velocity profile and average pressure drop is also governed by the types of flows and are being assumed for different sections. The pumps and other machineries play an important role in the flow of water through the pipes, controlled by valves/recycle valves. There are various studies on selection of an optimal economical pipe sizes (diameter) for pressurized irrigation system. Some of them are presented and reviewed herein.

Featherstone and El-Jumaily (1983) developed a computer programming approach for the selection of an optimal diameter pipe networks by incorporating the various capital and operating costs. Valiantzas et al. (2007) used very simple empirical pipe selection methods based on arbitrary concepts, which do not lead to an optimal solution instead. They presented a simple method, which allows the user to determine directly the optimum pipe size to use in simple irrigation delivery systems with pumps. Two simulation models were developed by Calejo et al. (2007) for the analysis of pressurized irrigation systems (sprinkling or micro-irrigation) operating on-demand to deliver water with the flow rate and pressure required with respect to the time, duration, and frequency decided by the farmers. Pedras et al. (2008) developed a decision support system (DSS) to design micro-irrigation systems and to advise farmers based on field evaluations. It was written in Visual Basic 6.0 language, runs in a Windows environment, and uses a database with information on emitters and pipes available in the market. Akintola and Giwa (2009a) developed a computer-aided optimization technique for the determination of optimum pipe diameter for a number of idealized turbulent flows. Relationships were formulated by connecting theories of turbulent fluid flow with pipeline costing. Akintola and Giwa (2009b) worked on an iterative optimization procedure for laminar flow in pipelines for the selection of optimum pipe diameter. Ohirhian and Ofoh (2010) developed various equations for direct calculation of the volumetric flow rate during laminar and turbulent flow of an incompressible fluid in pipes. The various equations were derived from simultaneous solution of the Bernoulli equations of Hagen Poiseulle and Darcy-Weisbach formula for the head loss and the Reynold’s number.

The aforementioned literature review indicates that most of the works regarding the optimization of pipe sizes selection was done by computer simulation models, which was not feasible for most of the Indian farmers as well as the farmers from Odisha. The average per capita water availability (both surface and ground) here is 3359 m³ per year (www.dowrorissa.gov.in). With the projected future application of Odisha, the per capita water availability will reduce to 2218 m³ in 2051, which is much above the water stressed condition of 1700 m³, and 1000 m³ was considered as water scarce condition (Water Resources Department, Government of Odisha, August, 2007). Odisha is primarily an agrarian state, where irrigation sector holds a key position in the economic development of the people and state as a whole. The application of pressurized irrigation systems for the irrigation and other purposes can neutralize the overload of water distribution in various sectors like, industrial sectors, domestic purposes, etc. One of the major criteria in the pressurized irrigation, selection of optimum pipe sizes considering the economic indicator is very important.

Variable costs of irrigation projects

 

Variable costs of irrigation projects include the cost on regulation of the conveyance system as well as maintenance and repairs. In case of wells and pumps, they include the cost of power/fuel (electricity/diesel), costs of lubricants, labour charges for operating the pumping units, and the expenditure on repairs and maintenance of the equipment and accessories. The cost of power is often the most important component of variable costs in the case of pumping systems. The usual practice is to calculate the requirement of energy per hour of operation from the known discharge rate of the pumping plant, total operating head and its overall efficiency. The requirement of power is expressed in kilowatt-hours for electricity and liters of diesel per hour of operation of engines. The energy consumption of an electric motor is computed as follows:

 

 

Efficiencies of electric motors may be obtained from the performance data supplied by the manufacturers. Motor efficiencies usually vary from 75 to 90%. The demand of electrical power for hourly operation is multiplied by the annual hours of operation to arrive at the total annual energy consumption. The annual power cost is determined by multiplying the annual energy demand by the prevailing cost per unit of electrical energy. Variability in expected life can occur for many of these components. Due to different physical conditions like the quality of ground water, the level of repair, operation and maintenance practiced, and the length of time, the system is used each year. In case of poor quality ground water and abnormal working conditions like excessive silt-load in water, the expected service life will be less. Sound engineering judgment should be exercised in estimating the economic life during the analysis.

 

Discounting rate, present worth, and capital recovery factor

 

The present worth is determined by multiplying the future amount by the expression:

 

 

The present worth of a future value at the end of n^th period at an interest rate of i is computed using the following formula,

 

 

 

It may be seen that the capital recovery factor (CRF) is the reciprocal of the present worth of an annuity factor. The compounding factor is used to calculate the future worth of a present amount at the end of a particular period, using the following relationship:

 

 

Where i = the discount rate indicating the opportunity cost of the capital. Discount rate is also called discount factor or present worth factor. (It is the reciprocal of the compounding factor for 1). The mathematical expression for compounding factor is:

 

(1 + i) ⁿ,

 

Where   i = rate of interest, n = period, PV = present value of the future income stream, F = future value of the income stream, A = amount of each payment, F_V = future worth, P’ = present amount, and P = present worth of a sequence of level payments.        

 

Capital recovery factor

 

Capital recovery factor (CRF) is used to calculate the amount of each level payment to be made at the end of each ‘n’ period, to recover the present amount at the end of the period, at a predetermined interest rate of ‘i’. The factor is computed as follows:

 

 

The amount of the level (even) payments to be made is computed by the formula:

 

 

Where A = amount of each level payment to be made at the end of each of ‘n’ periods, P = present amount. The annual cost of capital investment for an irrigation system can be determined from the present worth value of the investments, plus the interest during the period of analysis. The annual cost is usually determined by calculating a uniform series of annual values for depreciation and interest over the analysis period which is equivalent to the single present worth value. The value of this uniform series of annual cost is determined by the application of capital recovery factor (CRF).

 

Operating costs

 

Energy/fuel consumption

 

Electricity motor: Efficiencies of electric motors usually vary from 80 to 90%.

 

Energy consumption, kilowatt-hours =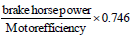 

 

Engine: An estimate of the rate of fuel consumption for a given engine can most accurately be made if the manufacturer’s fuel consumption curve for that engine is available. Cost per hour of operation:

 

 

 

Fixed and operating costs

 

The fixed cost (C_f ) for a pipeline, L is expressed as:

 

 

 

The operating cost (C_o) also depends upon on the following factors:

 

 

Annual operating cost to overcome friction is:

 

 

On substituting the value of h _f = 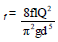 in equation (9),

 

 

Power loss due to friction (PS) in horse power is calculated as:

 

 

Annual power loss due to friction (PS) in kilowatt-hour is calculated as:

 

 

 

Substituting the value of C_f and C_o respectively,

 

 

The total cost per unit length of pipeline is,

 

 

Where d- diameter of pipe (m), Q = discharge (cumec), h_f = head loss due to friction (m), t = pump use hr/year , c_e = cost of electricity (Rs/KWH), 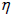= efficiency of power unit (fraction), W = Unit weight of water (kg/m³), P = price per unit length of pipe (Rs/m), i = interest rate, (fraction), n = life of pipe (years), C_T = _total cost per annum (Rs/year), C_f = fixed cost per annum (Rs/year), C_o = Operating cost per annum (Rs/year), and L = length of pipe (m).

 

Economical pipe size selection

 

Optimization analysis

 

The optimum diameter of pipe will be that diameter at which the present value of capital cost and operation and maintenance charges is minimum. Capital cost includes cost of pipes, cost of laying the pipe and the cost of pump set. The operation and maintenance (O & M) charges comprise of energy charges, and establishment costs pertaining to rising mains. Since the horse power of the pump sets depends upon frictional loss, energy charges are also a frictional loss, energy charges are also a function of the pipe diameter. The formula for determining the present value for the purpose of optimization analysis is given as follows:

 

 

Where i = rate of interest as applicable, and n = life of the project.

 

By minimizing the present value, optimum diameter is estimated and results for different discharges and types of pipes are computed and compared for their relative costs. The diameter of the pipe selected should be nearest to the optimum size thus arrived at.

 

Cost of pipe diameter relationship

 

In this, different pipes of varying sizes and materials, their price per unit length are considered. The prices for the different pipe materials have been obtained by collecting from various retailers and shops or standard farms. An empirical equation relating price with diameter which is used here is:

 

 

where P = price per unit length (Rupees), d = diameter (mm), a and b = constants. The criteria for deciding the most economical pipe diameter is that the diameter at which the sum of fixed and variable costs per annum is minimum. The total cost consists of fixed cost and operating cost. The fixed cost depends upon the initial value and life expectancy of the equipment. The variable cost is a function of head loss (h_f); flow rate (Q), the number of hours the system used in a year. The value of (h_f) was obtained from Darcy Weisbach formula, getting the value of Moody’s diagram and the empirical relationship between price per unit length and diameter was substituted to give an equation which can be differentiated with respect to diameter and equated to zero to yield the most economical diameter.

Empirical formulation of cost diameter relationships of pipes

 

To derive an exponential based mathematical equation between cost and diameter, various pipe diameters of different materials were selected. The different pipe materials include: reinforced cement concrete non pressure (RCC-NP2), RCC-NP3, galvanized iron, poly vinyl chloride (PVC) grey plain, PVC grey socket, and PVC grey rubber riveted (RR) joint. Each pipe material with diameters 40, 50, 75, 90,110, and 160 mm were selected to derive mathematical formulae. The prices for the different pipe materials of varying sizes were collected from various retailer shops and standard farms. The present costs of different pipes such as RCC, GI, and PVC are shown in Tables 1 to 3, respectively. The cost and diameter relationship of pipes is shown in Table 4. From this table, it is evident that there exists an exponential relationship between the cost and diameter of different pipes. Further, a value of coefficient of regression (R²) was derived for different pipe materials. The RCC- NP3 pipe material exhibited a highest value of R² = 0.986 as compared to other materials. The PVC Grey Plain pipe material exhibited a lowest value of R² = 0.941 as compared to other materials. However, there was not much difference in R² values were observed among different materials. Therefore, from these results one can say that the RCC- NP3 is the best material to consider for pipe construction during installation of pressurized irrigation system in the study region.

The cost and diameter of various pipes of different materials were plotted in the form of exponential plots and are shown in Figures 1 to 6. From the representation of the exponential plots, power curve equations were developed between the present cost (P) and diameter of the pipe (d) manufactured with different materials along with the coefficient of regression (R²) values. Trend lines were also plotted in Figures 1 to 6. From these plots, it is evident that the RCC- NP3 plot (that is, Figure 2) developed a well as established power curve relationship with highest R² value. The similar type of results was also drawn from the Table 4.

 

 

 

 

 

 

 

 

 

 

 

 

Economic analysis

 

The selection of pipe size of pumping plants and pipelines should be based on careful economic analysis. A small pipe may require a lower initial investment but the head loss due to friction is greater and this increases the power cost. A larger pipe in many cases will save more in power cost than the additional investment. Further, the larger pipe may so reduce the total pump head that a lighter and lower priced pump and power unit may be used. The actual cost of the installation based on the cost of pump and electric motor, taking into account the friction head under the two cases, should be estimated and the choice of the pipe size finalized. There are two types of costs are involved in deriving cost analysis i.e. fixed costs and operating costs. The fixed cost of the selected pipes was formulated considering the cost diameter relationship through equation (8) the fixed costs for the selected pipes are given in Table 5. The operating cost indicates the amount of power consumed while operating the power system for overcoming the frictional head losses in various pipe sizes. It has been evaluated on yearly basis, which decreases with increase in pipe diameter in all types of pipes. The operating cost depends upon the various factors, such as diameter of the pipe, discharge rate, head loss due to friction, pump operation hours in a year, cost of electricity per kilowatt hour, and efficiency of the power unit. The annual operating costs for various pipes of different variable sizes are calculated following equation (10), and is given in Table 6.

 

 

 

Irrigation system design substantially affects application efficiency and involves numerous variables, whose principal objective is to maximize benefits and minimize costs. The pressurized irrigation system can attain a reasonable level of efficiency, when they are well designed, appropriately selected, and adequately operated. The work was initiated with the collection of present rates of the selected pipes from the nearby market of Bhubaneswar, Odisha. The cost and diameter relationship of different pipe materials was established by developing an empirical equation in the power form. The fixed cost is calculated by using the present market value of the pipes the capital recovery factor per unit length of the pipe. The operating cost is calculated considering the variable diameters, flow rate, head loss due to friction, time of operation per annum, cost of electricity per annum, and the efficiency of the power unit. The cost is considered for the mathematical model (C_T = C_o + C_f). Thus, the mathematical model for the economical diameter was obtained. The minimum pipe sizes selection involves low fixed cost but result in high frictional head loss which results is more power consumption resulting is the high cost of operation. Again the selection of high pipes sizes results is high initial cost but less operating cost.

The authors have not declared any conflict of interest