Tunisia olive production fluctuates yearly because it is highly dependent on annual precipitation, and growers need to enhance productivity and efficiency by introducing irrigation. Investigating how irrigation affects the technical efficiency of olive production may contribute to improvement in productivity. This study employs the Data Envelopment Analysis (DEA) and Stochastic Frontier Analysis (SFA) methods to estimate non-parametric and parametric frontiers for a sample of Tunisian olive orchards. It identifies factors which determine variations in technical and scale efficiencies among orchards. The DEA results show that average output-oriented technical efficiency under constant returns to scale (CRS) and variable returns to scale (VRS) is 8.9 and 17.8%, respectively. The SFA results show that average technical efficiency of the half-normal model with constant returns to scale is estimated at 81.2%, indicating Tunisian olive growers can raise output by an average of 18.8% by improving technology and using fewer inputs. Average technical efficiency in irrigated orchards under the DEA approach was higher than in irrigated ones while irrigated orchards under the SFA approach was less technically efficient than non-irrigated ones. However, the test results of mean difference indicate that average VRS technical and scale efficiencies in irrigated orchards under the DEA approach were not significantly higher than in non-irrigated ones. On the other hand, technical rather than scale inefficiency is the major source of overall inefficiency in irrigated orchards because room for improvement in technical efficiency was larger than in scale efficiency. These results suggest that Tunisian olive growers should raise output and efficiency by introducing more advanced technologies for improving the performance of irrigation systems.
Key words: Olive orchards, technical efficiency, scale efficiency, irrigation, Tunisia.
In Tunisia olives are vital to the domestic economy and financial resources, especially in impoverished rural areas, accounting for 15.7% of Tunisia’s agricultural production in 2013 (NIS, 2016). Also, promoting exports of olive oil is central to Tunisia’s national development strategy following the Euro-Mediterranean Partnership eliminated export quotas, tariffs and trade barriers on agricultural commodities. According to Food and Agriculture Organization of the United Nations (FAO) statistics, the export of olive oil occupies 19.7% of the country’s agricultural exports in 2013. Therefore, enhancing productivity and technical efficiency has become a primary challenge for Tunisia’s olive growers. Tunisian olive production fluctuates yearly because it is highly dependent on annual precipitation. To stabilize and increase production, the Tunisian government encourages olive growers to introduce irrigation and to increase the proportion of their orchards under irrigation. Given the country’s limited water resources, investigating how irrigation affects the technical efficiency of olive production may contribute to improvement in productivity.
Limited studies have investigated productivity in olive-growing farms. Tzouvelekas et al. (1999) and Tzouvelekas et al. (2001) estimated technical efficiency among Greek olive growers, and Artukoglu et al. (2010) carried out the same for Turkey. Lachaal et al. (2005), Chemak (2012) and Kashiwagi et al. (2013) analysed the productivity and technical efficiency of Tunisian olive orchards. Most of the previous studies have investigated technical efficiency, while the effects of unconventional inputs (e.g., irrigation) and conventional ones (e.g., land, labour and capital) as factors to improve technical efficiency have not been well examined in the previous studies.
The objective of this study is to investigate how the introduction of irrigation affects the productivity and technical and scale efficiencies of Tunisian olive production by estimating non-parametric and parametric frontiers for a sample of olive orchards, located in four governorates in Tunisia; to quantify the technical efficiency of irrigated and non-irrigated orchards using Data Envelopment Analysis (DEA) and Stochastic Frontier Analysis (SFA) methods; to identify factors which determine variations in technical and scale efficiencies among orchards; and to compare the results from the DEA and SFA approaches to estimate non-parametric and parametric frontiers for a sample of Tunisian olive orchards. Our study contributes to the literature on the productivity and technical efficiency of olive orchards in Tunisia, the effect of irrigation on productivity and production efficiency and the methods to estimate production function frontiers for olive orchards.
Study area and sample size
Our survey was conducted in Beja, Nabeul, Sousse and Kairouan Governorates during the period from March to December 2011 (Figure 1). Beja Governorate in North-western Tunisia covers 3,740 km2 and has a population of 303,032. Nabeul Governorate in north-eastern Tunisia covers 2,788 km2 and has a population of 787,920. Sousse Governorate in eastern Tunisia is 2,669 km2 with a population of 674,971. Kairouan Governorate in central Tunisia comprises 6,712 km2 and 570,559 people. We selected olive orchards randomly directed questionnaires to their growers. Of the 167 responses collected, we have chosen 118 from 17 administrative divisions within four governorates. Table 1 shows the frequency distribution of the 118 orchards by governorate and by hectares under olive cultivation. As indicated in Table 1, 42.3% of orchards (50 orchards) are 5 ha or smaller, 28.0% (33 orchards) are 5 to 10 ha and 29.7% (35 orchards) exceed 10 ha. Summary statistics are presented in Table 2.
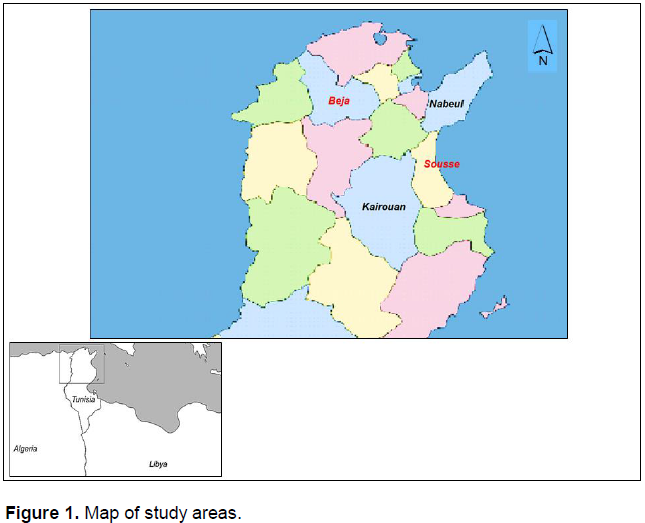

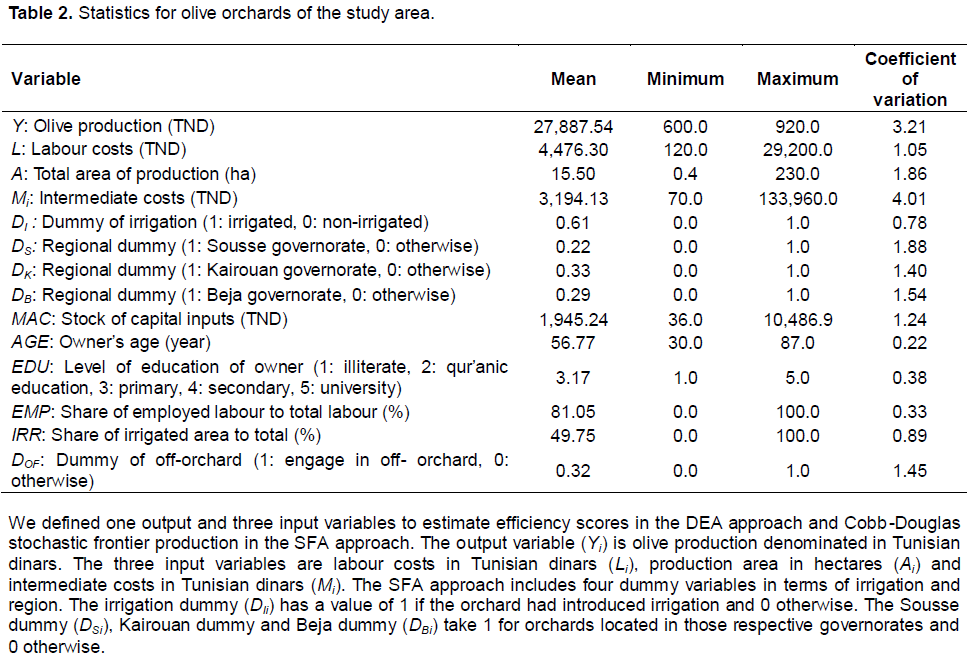
We defined one output and three input variables to estimate efficiency scores in the DEA approach and Cobb-Douglas stochastic frontier production in the SFA approach. The output variable (Yi) is olive production denominated in Tunisian dinars. The three input variables are labour costs in Tunisian dinars (Li), production area in hectares (Ai) and intermediate costs in Tunisian dinars (Mi). The SFA approach includes four dummy variables in terms of irrigation and region. The irrigation dummy (DIi) has a value of 1 if the orchard had introduced irrigation and 0 otherwise. The Sousse dummy (DSi), Kairouan dummy and Beja dummy (DBi) take 1 for orchards located in those respective governorates and 0 otherwise.
Model: DEA approach
The DEA approach measures relative efficiency. Proposed by Farrell (1957) and expanded by others, DEA mathematical programming allows researchers to construct a non-parametric piecewise frontier that includes input and output data. These data indicate which costs are minimized to calculate efficiency scores for each observation. As it is used here, the technique creates a frontier set of efficient olive orchards and compares it with inefficient orchards to produce efficiency indices. Olive orchards are given between 0 and 1, with completely efficient orchards scoring 1.
The DEA approach shows how one decision-making unit (DMU) (an olive orchard) manages relative to others in the sample and provides a benchmark for best practice technology from the experience of the sampled orchards. The DEA can estimate efficiency under the constant returns to scale (CRS) and variable returns to scale (VRS) hypothesis. The CRS assumption is appropriate only if all surveyed olive orchards operate at optimal scale. Obviously, many factors may cause olive orchards to operate below their optimal scale, and the CRS specification obscures the measures of technical and scale efficiencies in those cases. The DEA uses sample data to derive the efficiency frontier against which each orchard is assessed. No explicit functional form for production need to be specified. Instead, the production frontier includes piecewise linear segments that assign efficiency scores for each orchard. Here, an output-oriented model is used because an increase in olive production is the main objective in our study.
The DEA considers the technological phases of production function. This is unitized to estimate the cost and revenue frontiers, convenient for decomposing production efficiency into technical and scale efficiencies without requiring estimates of input and output prices. As to N DMUs in the olive-growing industry, all sample inputs and outputs are characterized by K and M, respectively. The efficiency of each orchard is then calculated by
Where θs is a scalar of the sth olive orchard, and λ is an N×1 vector of constant; and X is a K×N inputs matrix, and Y is an M×N outputs matrix. The first constraint shows that production of the ith output by observation s cannot exceed any linear combination of output by all orchards in the sample. The second constraint includes the use of inputs by observation s. 1/θs is the overall technical efficiency score for the sth orchard that satisfies: 1/θs < 1, where a value of 1 indicates the point on the frontier. 1/θs = 1 indicates that the orchard is technically efficient.
Second, when not all orchards operate at an optimal scale, the CRS DEA model is extended to the VRS DEA model. Technical efficiency is given by 1/Ï•s for the sth olive orchard. If calculated technical efficiency in the CRS DEA model differs from that in the VRS DEA model, the orchard has scale inefficiency. This means that scale efficiency (σs) is calculated by θs/Ï•s. Hence, the use of VRS specification permits calculation of technical efficiency devoid of the scale effect. That is, it decomposes technical efficiency into pure technical efficiency. The CRS linear programing problem can be modified into the VRS linear one by adding the convexity constraint:
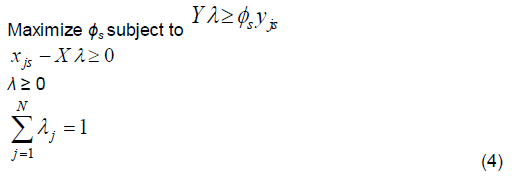
Where Ï•s is a scalar of the sth olive orchard. This approach constructs convex hull intersecting planes that envelop data points more tightly than under CRS. For instance, scale efficiency equals 1 if and only if the technology exhibits CRS specification. However, scale inefficiency may exist because of either increasing returns to scale (IRS) or decreasing returns to scale (DRS). In order to obtain these results, the solution to the VRS linear programming problem (4) must be restricted with the sum of the λ from 1 to N.
Data Envelopment Analysis Program (DEAP) Software Version 2.1 is used for measuring the technical and scale efficiencies in the DEA.
Model: SFA approach
A commonly used technique to parametrically estimate production function and to measure firm-level technical efficiency is the stochastic frontier method (Aigner et al., 1977; Meeusen and van den Broeck, 1977). This approach is frequently applied for agricultural farms to estimate inefficiency effects to capture the stochastic nature of agricultural production. A general form of stochastic frontier production function can be expressed as follows:
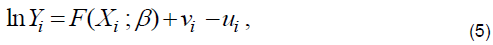
Where Yi is the output of the ith orchard; Xi is the vector of input quantities used by ith orchard; b is a vector of unknown parameters to be estimated. The term vi represents random disturbance terms, assumed to be an independent and identically distributed N (0, σv2). The term ui is a non-negative variable representing inefficiency in production relative to the stochastic frontier. It is assumed to be independently and identically distributed, that is, ui ~ iid N (0, σu2), which could be half-normal at 0 mean, truncated half-normal (at mean µ) and exponential (Aigner et al., 1977; Meeusen and van den Broeck, 1977; Stevenson, 1980; Jondrow et al., 1982; Greene, 1990) introduces a gamma distribution model.
For the estimation of stochastic frontier model, we employ Cobb-Douglas form of production function. Following Okikie et al. (2004), the effects of inputs on productivity in different conditions are explicitly incorporated in the production function using fixed-effects method. The binary dummy of irrigation is explicitly inserted in order to capture the impact of irrigation on productivity. Also, three regional dummies are used for controlling the difference in general environmental conditions in each particular country of Tunisia. The stochastic frontier production function is specified:
Where β0 is the intercept term; βi (i = l, a, m) and λi (i = I, S, K, B) denote unknown parameters to be estimated corresponding to three intermediate input variables (costs of fertilizer, pesticides, water and transport) and four dummy variables in terms of irrigation and region (Sousse, Kairouan and Beja), respectively.
Following Battese and Coelli (1995), the technical inefficiency effects, ui could be further expressed as a linear function of explanatory variables, reflecting orchard-specific characteristics. The inefficiency component of the stochastic frontier can be specified:
Where δ0 is the intercept term; δh (h = 1,…,6) is a vector of unknown parameters to be estimated. zhi is a vector of explanatory variables associated with technical inefficiency in production. wi is a random variable. From Equation (7), the inefficiency effects to be estimated are defined follows:
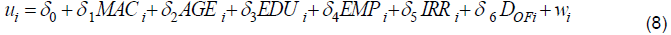
Where MACi is the stock of productive capital inputs (including tractors, cultivators and sprayer); AGEi is the owner’s age; EDUi is the discrete variable that represents the owner’s education on a scale of 1 to 5 (1: illiterate, 2: qur’anic education, 3: primary, 4: secondary, 5: university). EMPi is the share of employed labour to total labour. IRRi is the share of irrigated area to total (IRRi has a value of 0 if the orchard had not introduced irrigation). DOFi is the off-orchard dummy, which equals 1 if the orchard engages in non-agricultural activities and 0 otherwise. The parameters of both the stochastic frontier and the inefficiency effects can be estimated consistently by maximum likelihood (ML) procedures.
DEA approach
The CRS and VRS DEA models are estimated using the DEAP for efficiency measurement. Table 3 indicates the estimated frequency distribution and scores of technical and scale efficiencies. The average scores for CRS and VRS technical efficiencies are 0.089 and 0.178, respectively. One orchard was identified as fully technically efficient under CRS specification and eight under VRS specification, respectively. These results mean that olive orchards in Tunisia could increase production on average by 91.1% (0.911 = 1 - 0.089) and 82.2% (0.822 = 1 - 0.178), respectively, to reach full technical efficiency.
The average score of scale efficiency is 0.743. Three orchards were identified as fully scale efficient. Also, number of olive orchards operating under IRS, CRS and DRS as a percentage of the total is 62.7, 12.7 and 24.6%, respectively.
This reflects that 87.3% (103 orchards) of the olive orchards in the sample can enhance overall efficiency by improving scale of production. Specifically, the majority of olive orchards can achieve it through increasing scale of production. However, improvement in scale of production under IRS may have less effect on overall efficiency than under DRS because the average score of scale efficiency is close to 1 compared with that for orchards operating under DRS.
On the other hand, the average score of VRS technical efficiency for orchards operating under CRS is 0.099, which is lower score than that under IRS and DRS. This result shows that even the fully scale-efficient orchards need to enhance overall efficiency by improving their technical efficiency. Consequently, substantial inefficiencies occur in the surveyed area and technical rather than scale inefficiency is the major source of overall inefficiency because room for improvement in technical efficiency is larger than in scale efficiency.
Table 4 shows the efficiency scores by governorate. Olive orchards in Sousse are the highest average technical efficiency scores under VRS specification. On the other hand, olive orchards in Beja are the lowest. Specifically, orchards operating in Beja and Keirouan require to substantially improve their technical efficiency. Also, olive orchards in Kairouan are the highest average scale efficiency scores, while olive orchards in Nabeul are the lowest. One orchard in Sousse and two orchards in Kairouan are operating at optimal scale.
Most noteworthy about the average score for VRS technical efficiency is that orchards in the surveyed areas are producing only 17.8% of the maximum output levels for the existing inputs. This result shows that substantial improvement is needed to increase technical efficiency.
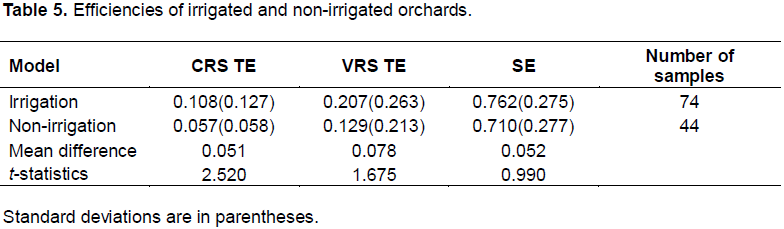
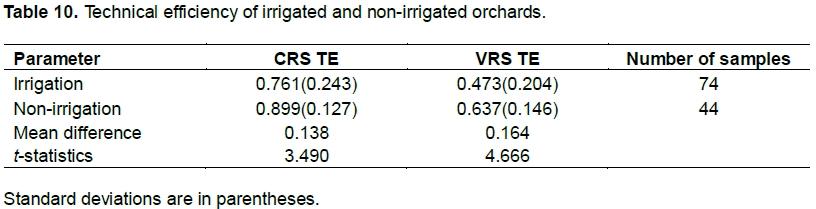
Table 5 includes the effect of irrigation systems on average efficiency scores and test of mean differences in the average level of efficiency. In the irrigated orchards of each governorate, average technical efficiency scores under CRS and VRS specifications were 10.8 and 20.7%, respectively. These empirical findings reveal that average efficiency in irrigated orchards exceeds that in non-irrigated ones. Also, most of the fully technically efficient orchards under CRS and VRS specifications and scale-efficient orchards had introduced irrigation. Three orchards are identified as fully scale-efficient. The statistical tests confirm that mean difference of efficiencies between irrigated and non-irrigated orchards is statistically significant for only the average score for CRS technical efficiency, while there is no significant difference in the average level of VRS technical and scale efficiencies. These results imply that irrigated orchards are not necessarily more technically and scale efficient than non-irrigated ones.
We assess effects on technical and scale inefficiencies using Tobit regression. As technical and scale efficiencies have the propensity to be censored at unity, we employ a standard Tobit model with upper censoring. Consequently, no inefficiency scores were less than 0. We estimate parameters in Tobit regressions using ML procedures. The technical and scale inefficiencies effectsto be estimated are defined as follows:
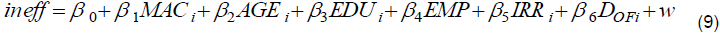
Where β0 is the intercept term; βi (i = 1,2…,6) is an unknown parameter to be estimated; and w represents the error term. The technical and scale inefficiencies effect is estimated using STATA 11 package. The results are indicated in Table 6.
Under CRS specification, only the estimated coefficients of AGE and IRR significantly affect technical efficiency. The estimated coefficient of AGE is negative and statistically significant at the 1% level: Older farmers are more efficient than younger ones. The estimated coefficient of IRR is negative and significant at the 5% level, suggesting that growers enjoy greater technical efficiencies as hectares under irrigation increase.
On the other hand, technical efficiency under VRS specification is significantly affected by the estimated coefficients of EMP, IRR and DOF. The estimated coefficient of EMP is positive and significant at the 1% level: the larger the share of employed labour in total labour, the less technically efficient is the orchards. This result implies that increasing the proportion of family members among total labour can boost technical efficiency. Our result disagrees with finding by Tzouvelekas et al. (2001), but, as noted by those authors, an agency problem may exist due to informational asymmetry between the parties. The estimated coefficient of IRR is negative and significant at the 5% level. The estimated coefficient of DOF is positive and significant at the 5% level: involvement in non-agricultural activities reduces technical efficiency.
SFA approach
Maximum likelihood estimates of parameters in the model of Cobb-Douglas stochastic frontier production are obtained using STATA 11 package. Table 7 displays parameter estimates and standard errors of the estimators. Although two models are estimated corresponding to the distributional assumptions of half normal and exponential for the one-sided error term (ui), a model estimated with the assumption of truncated normal distribution for the one-sided term could not achieve convergence; therefore, it is not reported. The information criteria are used for choosing the two models because the half normal distribution is not nested in the exponential distribution for the one-sided error term. Since the value of the criterion of the half normal model is marginally less than of exponential model, the Bayesian information criterion (BIC) favours half normal model. On the other hand, the constant returns to scale (CRS) hypothesis cannot be rejected by the F-test. Alternatively, the SFA model under CRS specification is estimated, assuming the half normal distribution of the one-sided error term. Since models estimated with the assumption of exponential and truncated normal distribution for the one-sided error term could not achieve convergence, both models are not reported. Therefore, results of the SFA model under variable returns to scale (VRS) and CRS specifications, assuming half normal distribution for the one-sided error term, are worth discussing.
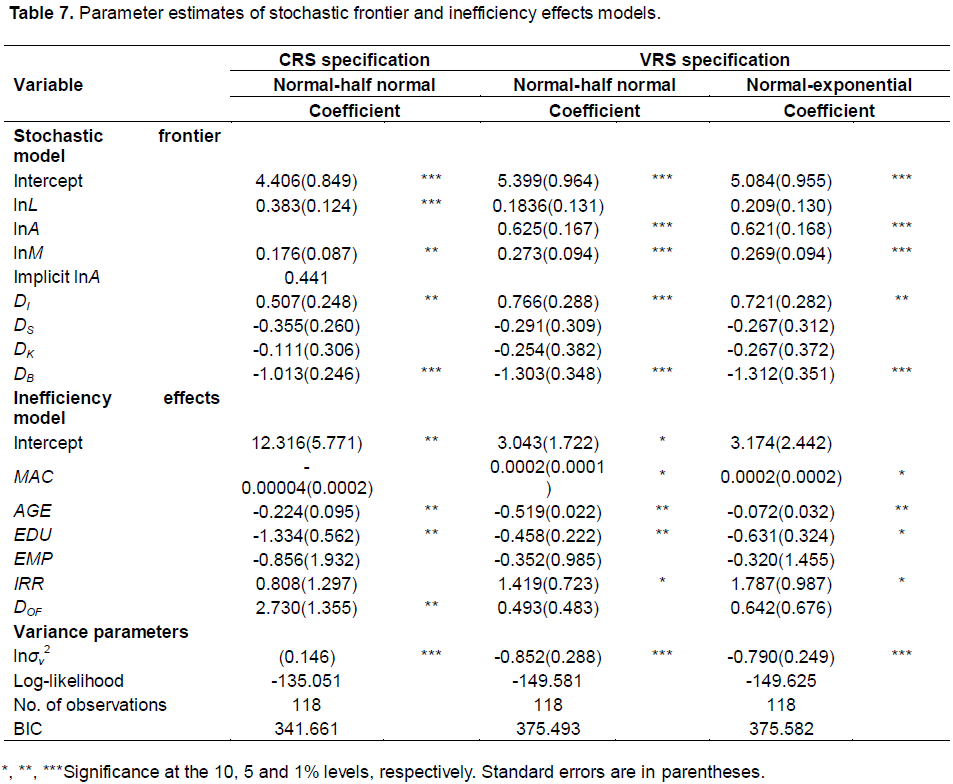
The results of model under CRS and VRS specifications show signs of estimated parameters are as expected. Estimated coefficients for intermediate inputs are positive and statistically significant in both models. The coefficient of labour is significant at model under CRS specification. In both models, land remains most important input in olive production. This significance of land input is similar to the results of Tzouvelekas et al. (1999), Tzouvelekas et al. (2001) and Karaginnis and Tzouvelekas (2001) for Greek olive orchards. The estimate of the irrigation dummy is positive and statistically significant at 1% level in both models. This result suggests irrigation significantly increases production. Also, this result is consistent with that of Lambarraa et al. (2007), which found a positive impact of irrigation in deterministic part of the production function for olive orchards in Spain. In this study, signs for regional dummies suggest that production is low in Beja compared with production in Nabeul.
In the inefficiency effects model, the estimated coefficients of AGE and EDU are negative and statistically significant in both models. These results suggest older and better-educated growers are more technically efficient producers, and low education restricts development of the sector. The positive effect of increasing age and education on technical efficiency is also confirmed by Karagiannis and Tzouvelekas (2001) for Greek olive orchards and by Lambarra et al. (2007) for Spanish olive orchards. The estimated coefficient for the stock of capital inputs (MAC) is positive and statistically significant in the model with VRS specification, while that of the model under CRS specification is not significant. These results suggest that mechanization is not a significant factor for upgrading efficiency. This result is not surprising and is similar to that of Tzouvelekas et al. (2001) for Greek olive orchards. The positive coefficient for the off-orchard dummy (DOF) in the model under CRS specification indicates that involvement in non-agricultural activities impairs technical efficiency. This result is consistent with Ali and Flinn (1987) which suggested off-orchard employment compete with on-orchard work.
Regarding the effect of the share of irrigated area (IRR) on efficiency, the estimated coefficient is positive and statistically significant at models under VRS specification but it is not significant at model under CRS specification. At least, these results imply that efficiency does not improve as the area under irrigation increases. This result is different from the finding by Lachaal et al. (2004), but alongside the positive sign for the irrigation dummy implies that irrigation contributes significantly to higher production. Its effect is significant for growth and olive production, but irrigation should be scheduled during suitable periods (Ahmed et al., 2007). However, we cannot confirm the positive effect of irrigation on technical efficiency and inefficiencies remain among some irrigated orchards. In addition, within the context of introducing technological innovations and efficient use of inputs, Tzouvelekas et al. (1999) point out that increased machinery inputs somewhat affect olive production in Greece if and only if they increased land productivity (that is, mechanised irrigation). Also, as shown by Chebil et al. (2014), the irrigation water use in Tunisian wheat farms is inefficient and the substantial decrease in water use could be attained by using the existing irrigation technology. Results for stock of capital inputs (MAC) and share of irrigated area (IRR) imply a need to introduce the modern irrigation technology that will raise land productivity. In fact, the use of innovative systems such as drip irrigation can increase yields and consequently incomes (Cetin et al., 2004).
The estimated frequency distribution of technical efficiency appears in Table 8. The average level of technical efficiency is 0.534 and 0.812 for models under VRS and CRS specifications, respectively. In the model under CRS, the level of technical efficiency ranges from a minimum of 0.138 to a maximum of 0.999. This estimated result of efficiency score is similar to other studies for Tunisian olive orchards. The average level of technical efficiency was estimated at 0.835 in Mehdia region (Lachaal et al., 2004), and samples from Sfax region was 0.82 (Lachaal et al., 2005). The estimated results of our study are based on the sample from Sousse, Nabeul, Kairouan and Beja. It suggests that the orchards can increase their production by 18.8% on average, given present state of technology and input levels.
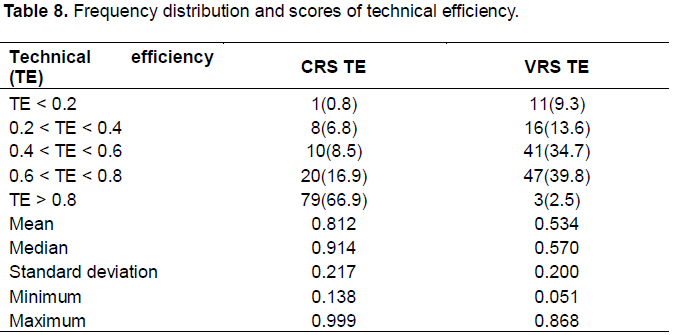
Table 9 presents frequency distribution of efficiency scores by region. Both models under VRS and CRS specifications suggest that the average level of estimated technical efficiency is the highest at Beja, while it is the lowest at Kairouan. In Table 10, results of comparison of efficiency scores between irrigated and non-irrigated orchards and tests of mean differences in the average level of efficiency are presented. The statistical tests suggest that mean difference of technical efficiency between irrigated and non-irrigated orchards is statistically significant for both half normal and exponential models. These results imply that irrigated orchards are less efficient than non-irrigated ones. These results also show the possibility of enhancing efficiency to upgrade the productivity and competitiveness. Indeed, improper use of irrigation systems could damage production efficiency. Growers need to schedule appropriately and have suitable knowledge of field conditions.
Figures 2 and 3 shows the relation between land productivity and technical efficiency for models under VRS and CRS specifications. It is noteworthy that production per hectare is higher in irrigated orchards in both models. However, technical efficiency varies among irrigated orchards and they are less efficient than non-irrigated ones. These results imply that introducing irrigation could potentially increase the level of production, but current production technology is somewhat distant from the best practices frontier.
Comparison between DEA and SFA results
This section reports the results from the DEA and SFA approaches that quantify olive orchards’ technical and scale efficiencies and identify factors which determine variations in efficiency among orchards.
First, the SFA model produces a higher average technical efficiency score than the DEA model. Specifically, the average level of technical efficiency under the DEA approach was much lower than that under the SFA approach. One explanation for this discrepancy might be a difference between deterministic and stochastic frontier estimations. On the other hand, the DEA approach is more sensitive to data noise, measurement errors and uncontrollable factors than the SFA approach. Therefore, it should be noted that efficiency scores obtained in the SFA approach cannot simply be compared with that obtained in the DEA approach. However, we can identify correlation between two approaches calculating the Spearman’s correlation coefficient based on rankings of individual orchard efficiency score under CRS and VRS specifications. Table 11 reports the correlation matrix. Efficiency scores in the DEA approach and efficiency ones in the SFA approach under VRS specification are lowly positively correlated with each other and significantly different from 0 at the 1% level, while no correlation exists between the DEA and SFA approaches under CRS specification. This result may imply that the sampled olive orchards operate under variable returns to scale or under increasing returns to scale rather than under constant returns to scale.

Second, results showing the effects of technical inefficiency in the DEA and SFA approaches were similar under CRS specification. Specifically, our econometric estimations show that nog-agricultural activities negatively affect technical efficiency, but the growers’ age and education positively affects it.
Third, estimated results for technical inefficiency differ between the two approaches. Although an increase in the share of irrigated area to total exhibits a significant positive effect on technical efficiency in the DEA approach, the opposite results were obtained in the SFA approach. In addition, average technical efficiency in irrigated orchards under the DEA approach was higher than in non-irrigated ones, while irrigated orchards under the SFA approach were less efficient than non-irrigated ones. However, the test results of mean difference show that there is no significant difference in the average level of VRS technical and scale efficiencies. This result implies a need to ascertain the efficient scale of production.
Unlike the SFA approach, the DEA approach estimates scale efficiency. However, Table 5 indicates that average scale efficiency in irrigated orchards under the DEA approach is not significantly higher than in non-irrigated ones. Also, it indicates that technical rather than scale inefficiency is the major source of overall inefficiency in irrigated orchards because room for improvement in technical efficiency is larger than in scale efficiency. Furthermore, Table 6 shows that technical efficiency under the DEA approach significantly rises as the area under irrigation increases, but the opposite results are obtained in the SFA approach. A difference between deterministic and stochastic frontier estimations might explain the discrepancy. As a consequence, irrigated orchards have not produced the maximum achievable output, but irrigated orchards enjoyed higher production than non-irrigated ones by introducing irrigation. Therefore, it can at least be stated that enhancing technical efficiency requires not only introducing irrigation but also improving current production technologies and irrigation scheduling. These results suggest that Tunisian olive growers should raise output and efficiency by introducing more advanced technologies such as drip irrigation and sprinklers for improving the performance of irrigation systems.
Our study has investigated how irrigation affects productivity and technical efficiency by estimating non-parametric and parametric frontiers. It quantified the technical and scale efficiencies of irrigated and non- irrigated orchards using the DEA and SFA approaches and identified factors which determine variations in technical and scale efficiencies among orchards.
The SFA approach exhibited a higher average technical efficiency score than the DEA approach. A difference between deterministic and stochastic frontier estimations might explain the divergence. Also, estimations of technical efficiency under the VRS DEA generally mirrored those of the SFA under CRS specification with the exception of results for mechanization, the share of employed labour in total labour and the share of irrigated area to total.
Average technical efficiency in irrigated orchards under the DEA approach was higher than in irrigated ones, while irrigated orchards under the SFA approach was less technically efficient than non-irrigated ones and the technical efficiency of irrigated orchards under the SFA approach varied across orchards. Also, average scale efficiency in irrigated orchards under the DEA approach was higher than in non-irrigated ones. However, the test results of mean difference indicated that average VRS technical and scale efficiencies in irrigated orchards under the DEA approach were not significantly higher than in non-irrigated ones. On the other hand, technical rather than scale inefficiency was the major source of overall inefficiency in irrigated orchards because room for improvement in technical efficiency was larger than in scale efficiency.
Consequently, irrigated orchards had not produced the maximum achievable output during the period of this study, but irrigated orchards enjoyed higher production than non-irrigated ones by introducing irrigation and thereby it could at least be stated that enhancing technical efficiency requires improving current production technologies and irrigation scheduling as well as introducing irrigation. These results suggest the need for technical and financial assistance from government and international donors to improve the performance of irrigation systems and to rectify inefficiencies in current production technologies.
The authors gratefully acknowledged that this study was supported by JSPS Grants-in-Aid for Scientific Research of Young Scholars (A), No.24683008 entitled: “Research on Development of Local Industry by Valorisation of Bio-resources in North Africa and Mediterranean Countries.”