Abstract

A sunflower (or ∆-system) with k petals and a core Y is a collection of sets S₁,⋯, S_k such that S_i∩S_j=Y for all i≠j; the sets S₁\Y,⋯, S_k\ Y, are petals. In this paper, we first give a sufficient condition for the existence of a sunflower with 2 petals. Let F={A,B,C} be a family of subsets of a set { a₁,⋯,a_m , b₁,⋯,b_n , c₁,⋯,c_n } with 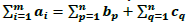 and A={a₁,⋯,a_m}, B={ b₁,⋯,b_n } and C={ c₁,⋯,c_n } are non-increasing lists of nonnegative integers. Suppose that for each r with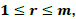 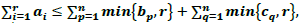   then the family F^* contains a sunflower with two petals, where F^*={G₁ ,G₂}, G₁=G[Y∪X] and G₂=[ Z∪X] are the subgraphs induced respectively by Y∪X and Z∪X with  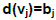for all v_j 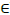Y∪X and  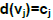 for all v_j 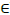Z∪X. Moreover, we generalize the consequence to the case of a much more general result.

Key words: Sunflower; family; tripartite graph.