Numerical methods for the solution of the initial value problems (IVP’s) are well established techniques in literature. In the last two decades, a number of papers have appeared on this topic (Abbas, 1995, 1997; Abbas and Delves, 1989; Voss and Abbas, 1997; Birta and Abou-Rabia, 1987; Chu and Hamilton, 1987; Enright and Pryce, 1987; Franklin, 1978; Henrici, 1962; Houwen and Sommeijer, 1989; Katz et al., 1977; Lambert, 1973; Luther  and Konen, 1965; Miranker, 1971; Miranker and Liniger, 1967; Moody and Hans, 1987; Moulton, 1926; Mouney et al., 1991; Rosser, 1967; Shampine and Watts, 1969; Watts and Shampine, 1972; Worland, 1976; Adesanya et al., 2013; Dhaigude and Devkate, 2017; Adesanya et al., 2013). The earliest research on block methods was proposed by Shampine and Watts (1969) and Watts and Shampine (1972) with block implicit one step methods, Chu and Hamilton (1987) with multi-block methods, and Voss and Abbas (1997) with predictor-corrector schemes. Other block methods are discussed by several researches such as Houwen and Sommeijer (1989) with block Runge-Kutta methods. One of such techniques is the block method which by means of a single application of a calculation unit yields a sequence of new estimates for y in the differential equation:

where 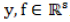. If the block size k ≥ 1, then in simple cases the values of x for which solutions are computed will be evenly separated. In other words, each basic cycle of calculation has the potential to advance the solution by k new points in the x direction. The block method of the present study has the properties of Runge-Kutta method for being self-starting and does not refuse the development of separate predictors or starting values. Block method was found to be cost effective and to give better approximation.

The requirement that the method be fifth order for any block length k complicates the search for good methods. The aim was to produce a fifth order method which might be very efficient to implement. As far as the order of the accuracy and the stability are concerned, if we require a method of order  to be achieved then the local truncation error will normally be of order 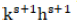 which is a very high dependence upon the block length k. We seek some methods where the local truncation errors have a lower power of k, as example, 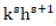, but then over experience with order 2 methods suggest that the stability problem will be possibly serious.

Therefore, we consider the fifth order method:

Tables 1 to 4 show the experimental results for the aforementioned test problems and the accuracy of the solution which is measured by computing the differences between the approximation solution and the exact solution at the end of the steps.

For all the problems tested, the numerical results show that new block fifth order method gives good accuracy with the reduction of total steps.

COMPARISON WITH A RUNGE-KUTTA METHOD OF THE SAME ORDER

Here, we compare the experimental results which was obtained by this study block method (with block length =

5) and the following fifth order Runge-Kutta method given by Luther and Konen (1965). From Tables 5 to 8, we notice that the accuracy is satisfactory and  much  better than the fifth order Runge-Kutta method. Note that the accuracy of the solution is measured by evaluating (l_∞) norm of the differences between the approximation solution and the exact solution.

This paper provides a new block method of higher order which can be implemented as a corrected formula of any block size together with Euler’s method as a predictor formula. However, this research is concerned with solving initial value problems using block predictor-corrector method of fifth order. The study highlights the importance of solving initial value problems and their application in the real life problems. Furthermore, the result indicates that the block method which was derived in the study could be considered as a good method on the basis of the accuracy and the comparison with a Runge-Kutta method of the same order. Also, we noticed that the accuracy is satisfactory and much better than the 5th order Runge-Kutta method. Thus, for small h we can say that the algorithm may give a better accuracy. Therefore, the results are acceptable.

The authors have not declared any conflict of interests.

The  authors  are  grateful  to  the  referees  for  the  very constructive comments and for suggesting various improvements to the manuscript.