To form the basis spin states of a field, vector states of the multicomponent wave function to the four coordinates of Minkowski space that determine the position of the local observer have been added by angular extra dimensions that determine the orientation of the local observer. The generators of the Poincare group in the angular representation have been obtained. The Dirac equation (generalized for any spin) and Maxwell’s equation have been designed from these generators. In the framework of transformations of the Lorentz group in angular representation united with its transpose representation, the transformations of the (generalized) Dirac equations that is similar to the Heaviside-Larmor transformations for Maxwell’s equations have been performed. As a result, the Dirac equation for the Dirac monopole, which corresponds to a particle with mirror symmetry have been obtained. Indication of a low probability of the existence of the Dirac monopole had been obtained.
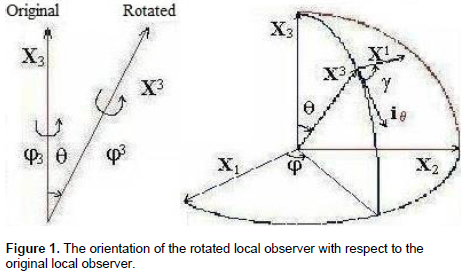
The meter is the original right Cartesian coordinate system. At the center of the point x1, x2 and x3 original local observer with unit vectors X1,X2 and X3 parallel to the meter were introduced. For describing objects with zero size at the center of the point x1, x2 and x3, a rotated local observer with unit vectors X(1),X(2) and X(3) and with the orientation defined by three independent Euler angles φ3=φ, φ(3)=γ with respect to the local original observer were introduced as shown in Figure 1. In fact, instead of one rotated observer are introduced a lot of rotated observers j, q and g. Turning one rotated observer means turning a lot of the multidirectional rotated observers. The superscript and the subscript in operators X(k), J(k), Ji, Q(k)i refer to respectively the rotated observer with unit vector X(k) and to the ordinary observer with unit vector Xi. The rotation matrix can be written in a symmetrical form with respect to the two local observers (Bidenhander and Lauk, 1984):
Rij=(X(i),Xj), (X(1),X(2),X(3))=R(X1,X2,X3)=R3(j) R2(q) R3(g).
X(1)1=–sin(q) sin(g)+cos(q) cos(j) cos(g), X(2)3=sin(q) sin(g),
X(1)3=–sin(q) cos(g), X(1)2=cos(j) sin(g)+cos(q) sin(j) cos(g),
X(2)1=–sin(j) cos(g)–cos(q)cos(j) sin(g),
X(2)2=cos(j) cos(g)–cos(q) sin(j) sin(g),
X(3)1=sin(q) cos(j), X(3)2=sin(q) sin(j), X(3)3=cos(q),
The generators of the rotation group Jk or angular momentum operators of rigid body will be called the generators of the vector rotations relative to the original local observer. The projections Jk onto the axis of the rotated local observer: J(k)=(X(k)J) are considered in literature as the operators of the angular momentum of a symmetric top. Let εi,j,k is the antisymmetric tensor ε1,2,3=1.
J1=i cos(j) ctg(q) ¶/¶j+i sin(j) ¶/¶q–i cos(j)/sin(q) ¶/¶g,
J2=i sin(j) ctg(q) ¶/¶j–i cos(j) ¶/¶q–i sin(j)/sin(q) ¶/¶g,
J(1)=–i cos(g) ctg(q) ¶/¶g –i sin(g) ¶/¶q+i cos(g)/sin(q) ¶/¶j,
J(2)=i sin(g) ctg(q) ¶/¶g – i cos(g) ¶/¶q – i sin(g)/sin(q) ¶/¶g,
J3=–i ¶/¶j,
J(3)=–i¶/¶g
[Ji, Jn]=ieink Jk,[J(i), J(n)]=–ieink J(k), [Ji, J(n)]=0 (1)
The operators J(n) are generators of the transposed rotation group, they are also generators of a group of rotations of the rotated local observer X(1),X(2),X(3) relative to himself. It is impossible to interpret the rotation by means of operators Jk by the rotation by means of operators J(n), as the operator Jk cannot be obtained from J(n) by using a unitary similarity transformation (Bidenhander and Lauk, 1984). The operators Jk=X(n)k J(n) are projections of J(n) onto the axis Xk and invariant under rotation using J(n). Vectors in coordinate system X(k) will be called isovectors and rotation using J(k) will be called rotation in the isovectors space. Wigner D functions, Djmm' are the eigenfunctions of the angular momentum operators J3, J(3), J2=Jk Jk. This corresponds to the symmetry between the original observer and rotated observer and so it is written in this form:
D*(1/2)=(x(1/2),x(-1/2)), x(1/2)=( y1, y2), x(-1/2)=(y3,y4).
y1=cos(q/2) exp(ig/2+ij/2),
y3=– sin(q/2) exp(–ig/2+ij/2) (2)
y2=sin(q/2) exp(ig/2–ij/2), y4=cos(q/2) exp(–ig/2–ij/2)
The known symmetry operator between the original local observer and the rotated local observer has the form W: j' =g, q' =-q, g' =j, (Bidenhander and Lauk, 1984) and formally implements permutation by the places of these observers. The operator W corresponds to the operation of transposition for the representation of a rotation group which is denoted by icon T. The icon -,* is the operation of complex conjugation. For example:
J(k)=(-1)k+1 W Jk, W Dj=DjT, X(k) n=(-1)k+n W X(n)k. (3)
The Euler angles φ, θ, and γ that determine the orientation of the local rotated observer relatively to the meter were named as extra dimensions to the four coordinates of the Minkowski space. The elements of the new space φ, θ and γ are Wigner D functions, Djm,m' which are transformed using the group SU(2). The double space of all possible orientations for the rotated observer corresponds to the space domain of the angles Wigner D functions with volume ∫∫dΩdγ=16 π2, dΩ=sin(θ) dθ dφ, Ω is a solid angle (Bidenhander and Lauk, 1984). The Wigner D functions, D(j), X(k)n are bases of orthogonal functions:
<ξ(m)i | ξ(k)n>=∫∫ξ(m)i*ξ(k)ndΩ dγ=δi,nδm,k /b2
where b=
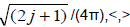
/(4π),<,> icons are used only for the orientations space, and δ
i,k is the Kronecker delta, δ
k,k=1. Any column ξ
(m') of the matrix D
(j)* is transformed in the same manner as a spinor j under spatial rotation and corresponds to a complete set of basis vectors describing states with spin j, (Varshalovich, 1975), as
Jξ
(m')T=ξ
(m')TS, [S
i,S
n]=ie
ink S
k, S
i is the matrix operator of angular momentum. The rotated observer for state j also as original observer has 2j+1 degrees of freedom corresponding to the analog of the spin projections m'=-j..,+j,
J(3) ξ(m')=m' ξ(m')
For example j=1/2, 2Sn=σn are Pauli matrices. Let ξm be any m string of the matrix Dj*. Using the operator W, the identities were obtained:
Taking into account the completeness of the system of bases Dj, any spinor j, ψT =(ψj, ψj-1, .., ψ-j) can be represented as a linear combination ξ(m') of the spinors j, which depend only on φ, θ and γ (Bidenhander and Lauk, 1984). The transformation using exponential operator is taken using the Baker-Campbell-Hausdorff formula:
ψ'=exp(A) ψ, exp(A)=1+A+A2/2!+A3/3!+..;
B'=exp(A) B exp(-A),
exp(A) B exp(-A)=B+[A,B]+1/2![A[A,B]]+1/3![A[A[AB]]]+..
The presence of well-known transformational properties of these bases of spinors ξ(m'), vectors X(k), (Bidenhander and Lauk, 1984) is based on the premise that the bases themselves are presented as the rotation matrix Dj, (R) under the turn of the original local observer onto Euler angles α,β and c.
Dj(φ',θ',γ')*T=Dj(φ,θ,γ)*T Dj(α,β,c)=
=(exp(-iα J3) exp(-iβ J2) exp(-ic J3)) Dj(φ,θ,γ)* T, (4)
Dj(α,β,c)=exp(-iα S3) exp(-iβ S2) exp(-ic S3).
The rotations of the original local observer (Equation 4) and the rotated local observer onto angles ω are also realized by the rotation operators exp(-iωJn) and exp(-iωJ(k)).
We have identities:
exp(-iω Jn) (X(p)1 ,X(p)2 ,X(p)3 )=(X(p)1 ,X(p)2 ,X(p)3 ) Rn(ω),
exp(-iω J(k)) (X(1)n ,X(2)n ,X(3)n )=(X(1)n ,X(2)n ,X(3)n ) Rk(ω)T
exp(-iω Jn) (ψ 1, ψ 2)=( ψ 1, ψ 2) exp(-iω σn),
exp(-iω J(k)) (ψ 1, ψ 3)=( ψ 1, ψ 3) exp(-iω σkT).
The known spatial transformation and Lorentz transformation can be obtained in two equivalent ways, both with the help of generators of the Lorentz groups and with the help of the transformation of angles φ, θ and γ which correspond to the transformations of the vectors X(1),X(2) and X(3). For example, rotating the meter around the x3 axis by an angle α is accompanied by a transformation of the angle φ'=φ-α, hence ξ(±1/2)'=exp(-iα σn/2)ξ(±1/2) is gotten. Assuming that the spinors ξ(±1/2) are a Weyl spinors which has the known Lorentz transformation with velocity, v=|v|x3, th(χ)=v/c, ξ(±1/2)m'=exp(±m χ)ξ(±1/2)m and taking into account the symmetry by angle φ, the following angular transformation were obtained: φ'=φ, γ'=γ, tg(θ'/2)=exp(-χ) tg(θ/2); and a scale transformation of the basis which is the same for each j, Dj, in the class 2j. Further, that this transformation does not change the orthogonality between the vectors X(n) can be verified. Substituting the Lorentz transformation of ψk into identity:
X(3)3=ψ1ψ4+ψ2ψ3, X(0)0=ψ1ψ4-ψ2ψ3, X(1)3=ψ3ψ4-ψ1ψ3, X(2)3=ψ3ψ4+ψ1ψ3, X(n)k=ψ2J(n) Jk ψ*T, ψ=(ψ1,, ψ2, ψ3, ψ4).
That the Lorentz transformation-X(3)3 ,X(0)0 and x3, t is realized in the same way as a four-dimensional vector x, t and X(3),X(0)0 has a length of zero was obtain. Also that X(1),-X(2) are transformed as bivector E and H of the electromagnetic field X(1)3=X(1)3', X(2)3'=X(2)3 was obtained. For a unified description of states with spin j, vector and tensor fields dependent on the orientation of the meter, we introduce the state of a class 2j, as a class of functions Ψ=ψ C which may be represented by a homogeneous polynomial of degree 2j of ψk, (2) (Varshalovich, 1975). This class corresponds to the principle of superposition of states. For example, the Wigner D function, Dj has a class 2j.The Lorentz transformation does not change the class2j of functions Ψ since ψk, (2), j=1/2 are linearly transformed. The introduction of the state of class 2j is also associated with the expansion of the description of spinors j under the Lorentz transformation and is also connected with the overcoming of the difficulties associated with the ambiguity of the transformations of the wave function from the angular variables and which is also of the analogous difficulties described in Cartan (1927) under the matrix interpretation. Example, under the Lorentz transformation of spinor j or Dj may appear additional summands (components) in the form spinor j-1, j-2 or X (0)0Dj-1, X (0)02Dj-2, where X (0)0=ψ1 ψ4-ψ2ψ4=1 is a dimensional unit function of class 2. These summands do not change the class and do not appear under the spatial rotations. In addition, the following operators can be formally represented in the identical ladder form that does not change the class (Jante and Schroers, 2016):
8J3=ψ1¶/¶ ψ1-ψ2¶/¶ψ2+ψ3¶/¶ψ3-ψ4¶/¶ψ4,
4J-=ψ2 ¶/¶ψ1+ψ4¶/¶ ψ3, 4J(+)=ψ1¶/¶ψ3+ψ2¶/¶ψ4
The states with spin 1/2 has the next unique property: In the summation of states ψ1, ψ2 (or ψ3, ψ4), C=(C1,C2), Ψ=C1 ψ1+C2ψ2 that corresponded to different orientations of spin, there is always such a rotated coordinate system X'k=C σk CT* in which the spin is described by C'=(1, 0) and Ψ has the same form Ψ=ψ1. There are only two independent forms (functions) ψ1 and ψ4 except for their linear combination, where ψ1=ψ4*. This property will be named to the property unchangeability of form of the angular function when similar states are added. A multicomponent wave function C=(Cj,Cj-1, ..,C-j)=Ck |k > corresponding to the spin (vector) states in the isotropic Minkowski space is proposed equivalently (one to one) to describe as a one-component wave function Ψ=Ck ψk space, where |k>=(0, ..0, 1, 0..0) is unit basis, Ck depends only on x1, x2, x3, t and ψk, depends only on φ, θ and γ. This corresponds to the replacement in the wave function of the matrix basis | k> by an operator basis ψk with the same transformation properties as for the matrix basis using group SU(2). φ, θ and γ may be interpreted as the possible orientation of the particle. The decomposition of Ψ in the basis ψk corresponds to the multicomponent wave function C.
Ci=<Ψ| yk>, J3Ψm=m ψm, CTC=<Ψ|Ψ>, <ψi |ψk>=δik.
For the physical meter in Minkowski space angular dimensions are hidden, internal and not observable, that is, all physical quantities at each point of space are calculated as average values over double the space of all orientations. The elements of the seven-dimensional space are the one-component wave functions Ψ=ψC. Spatial transformation properties of spinors C are provided by the choice of ψ in the form of the spinor as any a linear combination of spinors ξ(m'), j and Sommerfeld conditions, according to which the wave function Ψ=ψC must be invariant under the Lorentz transformations ψC=ψ'C'. Therefore, the transformation properties of basis ψ and C are related to each other, namely:
if ψ'T=U ψT, C'=V C then UT V=1, V=(U-1)T
The rotation matrices U and V are unitary matrices so V=U*. For Ψ=ψC the vectors ψ=X(k) and C have the same (identical) transformational properties as:
U=R(α, β, c)-1, V=R-1
For the spinor we have:
ψ'T=Dj(α,β,c)T ψT, C'=Dj(α,β,c)T* C,
(ψ1', ψ2')=(ψ1, ψ2) exp(-iω σn), C'=exp(i ω σn) C,
Lorenz transformation properties of spinor C are provided selecting ψ in the form specific of a linear combination of ξ(m'), j which satisfy the famous Lorentz transformations of the spinor C. All dimensions x1, x2, x3, t and φ, θ, and γ are mutually independent, but their transformational properties, except translation, are interconnected. The transformation properties of fields (vector, spin, etc.), except translation, are fully described the transformation properties of the basis functions of φ, θ and γ. Note that a field is present only in C, but ψ has no field, because φ, θ, and γ have no relation to the coordinates x1, x2 and x3 and to the position of the local meter. The initial values φ, θ and γ (countdown) are related only to the orientation of the meter. Generators of the group J(k), Jn, ¶/¶φ, ¶/¶θ and ¶/¶γ act only on basis functions ψ in Ψ=ψ C, but not on the field C. Each representation of spinors ξ(k), k=-j, .j , may have its own invariant Ψk=C(k)ξ(k) under spatial rotations. After completing the Lorentz transformation (Sventkovsky, 2004) for arbitrary spinor ξ(k) which is a basis of spatial rotations, the full extended Lorentz basis j was gotten. Moreover, the extended components of the basis are also spinors corresponding j'=j-1, j-2....., X(0)0ξ(n), X(0)02ξ(n).. The wave function Ψ of the class 2j can be composed of 2j+1 independent Lorentz invariants Ψ(j)k=C(k)ξ(k)+C(n)ξ(n) obtained from 2j+1 invariants of C(k)ξ(k), k=j, j-1, ..-j under spatial rotations, plus the invariant C(n)'ξ(n)'obtained via extended Lorenz basis ξ(k).
Theorem 1
A spatial inversion leads to internal inversion Î. á¹”: t'=t, x'i=-xi; Î:φ'=π+φ, θ'=π-θ, γ'=π-γ, which is a equivalent to the turn of the rotated local observer about axis X(2) by angle-π.This follows from the identities:
Î ξ(±j)=(-1)j _jξ( ), Î2 ξ(±j)=(-1)2jξ(±j),Ji=Î Ji, ÎX(k)=(-1)k
X(k),Î=exp(iπ J(2))
The law of conservation of parity is directly related to the conservation of symmetry between the left and the right. The bases Djm,m' and Djm,-m' are linked by inversion transformation Î Djm,m'=(-1)j-m'Djm,-m' . This allows to divide the entire basis into two equal groups of basis, except the case m'=0 for the whole j. The group of bases m'> 0 is called the left and its mirror m'< 0 is called the right. The difference (balance) between the left and the right, with weight m', is calculated as the average value of the operator J(3). For example:
Ψ=C(m') Djm,m'+C(-m') Djm,-m' , <Ψ|J(3)|Ψ>b2=m' (|C(m')|2-|C(-m')|2)
The complex conjugation operator has the form:
exp(iπJ(2)) exp(-iπJ2)Djm,m'=Djm,m'*.
The models of the electromagnetic field
In accordance with the quantum formalism, to describe the electromagnetic field, besides E, H we introduce the wave function in the form:
ΨEH=EX(1)+HX(2), ΨA=AX(3)+A0c X(0)0, F(1)=E, F(2)=H, F(3)=A, F(0)0=A0c, F(k)=b2<Ψ|X(k)>, F(±)=F(1) iF(2)
E, H and A, A0 may be considered as the amplitudes of the wave function of basic states of the electromagnetic field. The bases of the vector electromagnetic field directed along the axes of xk in the symmetric form X(n)k, X(0)0 with respect to two observers X(3), X3 have been found from the well-known transformation properties of the electromagnetic field and from the condition of invariance Ψ=ψ C. The bases X(n)k, X(0)0 correspond to a complete set of orthogonal basis functions for the state of the class 2j=2. The wave function, the electric field and the magnetic field has the form. Why is the sum of two electrical vectors equal to the electric vector? Because basis functions X(p)k, under their arbitrary addition at p constantly have property unchangeability, same functional dependence on angular dimensions (analog of property of form) in some rotated coordinate system, which always exists. Namely: for any vector states C=(C1,C2,C3), Ψ=CX(p), there is always such a rotated coordinate system X3'=C'/|C'| in which vector C'=(0, 0, |C|) and Ψ'=C'3X(p)'3. That is, Ψ' have the same functional dependence with X(p)3 . Example:
X(p)2=exp(iπ/2J1) X(p)3, X(p)1=exp(-iπ/2J2) X(p)3,
X(p)2=X(p)1(φ+π/2).
According to the principle of superposition of states, the addition of vectors of the electric field and of the magnetic field coincides with the addition of their models Ψ as a function of the angles φ, θ and γ. For example:
Ψ=EX(1), Ψ=HX(2), Ψ(E1)+Ψ(E2)=Ψ(E1+E2).
For the class 2, only vector basis, but not spin basis has this property of the same form. There are only three independent the forms for j=1, except for their linear combination, which correspond to three functions X(p)3 , p=1, 2, 3. The proof follows from the completeness of a 10-dimensional basis for class 2. For Y of class 2 there are only 3 Lorentz invariant (Sventkovsky, 2004):
C(±1)ξ(±1)=F( )X(±),C(0)ξ(0)+C(0)0 X(0)0=F(3)X(3)+F(0)0 X(0)0=ΨA
The real part of the invariants Ψ(±)=F( ) X(±) is obtained from the sum (difference) of the complex invariants, corresponds to the wave function of the electromagnetic field which has a zero projection of the (iso) vector operator Jk, J(n) at each point of Minkowski space.
Y=YEH=EX(1)+HX(2), YHE=-HX(1)+EX(2), <Y|Ji|Y>=0, <Y|J(n)|Y>=0.
The Lorentz transformations X(k) with the condition of Sommerfeld about the invariance of the wave function Y=E X(1)+H X(2), provide the well-known Lorenz transformation properties of the fields E,H,A,A0.
Y=YEH=EX(1)+HX(2), YHE=-HX(1)+EX(2), <Y|Ji|Y>=0, <Y|J(n)|Y>=0.
Mathematically the vectors can be added as objects having different directions, but in physics objects are always added as objects with one and the same direction. For example, a physical object is a set of projections of a vector. The addition of vectors will be regarded as the addition of a set of unidirectional projections. A vector has one to one correspondence with a set of its projections and vice versa. The projections are directed to the center of the vector for positive values of the projections and from the center for negative values. The basic states of the fields E,H,A which are directed along the axis x3, have the form:
X(1)3=-sinθ cosγ , X(2)3=sinθ sinγ , X(3)3=cosθ.
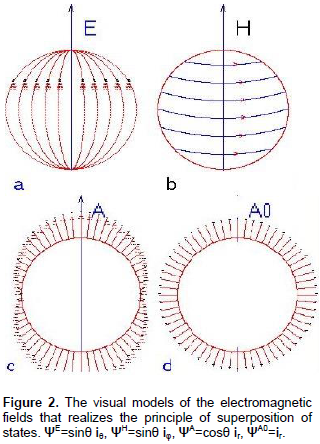
To visualize the model of basic states in the center of the local observer, imaginary sphere of unit radius X(3) is introduced; iθ, iφ, i3 are spherical orts, given:
X(1)(φ,θ, 0)=iθ, X(2)(φ, θ, 0)=iφ, X(3)(φ, 0,γ)=i3.
The vector iθ is assigned to the projection of cosγ on the sphere. The vector iφ is assigned to the projection of sinγ on the sphere. The vector i3is assigned to the projection of cos(θ), that are directed along ir. Then replace the cosγ on iθ in X(1)3 , sinγ on iφ in X(2)3 and X(3)3=cos(θ) will be considered as a set of projections of i3, directed along ir. The resulting visual model of the electromagnetic fields, correspond to a basis states X(1)3 ,X(2)3 ,X(3)3 and X(0)0 shown in Figure 2. The polarity of the vector of electric field, the axial symmetry of the vector of magnetic field has been reflected in this mode. E, H, A, A0 c and X(1),X(2),X(3),X(0)0 , under the spatial inversion are transformed identically Î X(k)=(-1)k X(k).
The generalized Lorentz group in the angular and matrix representation for transformations of spinors, tensors
The lie algebra of the groups Lorenz (Equation 5), Poincare (Equation6) and its generators in the coordinate representation (Ohnuki, 1988); L=(M23,M31,M12), K=(M01,M02,M03), where Mij=xi Pj-xj Pi, x0=t, and Pi =−i¶/¶xi, P0 =i¶/¶t are operators of momentum and energy, have the form:
[Li,Ln]=ieink Lk, [Ki,Ln]=ieink Kk, [Ki,Kn]=-ieink Lk. (5)
[Pi, Pk]=0, [Kk, Pk]=-i P0, [Li, Pn ]=ieink Pk, [Ki, P0]=-i Pi. (6)
Operators Q(p)k(φ,θ,γ) have been introduced (Sventkovsky, 2004) in a symmetric form as a vector for the lower indices and an isovector for the upper indices, that is,
Q(p)=i X(p) Ä´+[X(p)J], Q(p)k=i X(p)k Ä´+eink X(p)i Jn= iX(p)k-einp X(i)k J(n)
Ä´ is a linear, differential scalar Lorenz invariant operator that has properties: Ä´ Ψ=j Ψ for class 2j. It is possible because the Wigner Dj function can be decomposed into a homogeneous polynomial of degree 2j from ψk (Equation 2), (Varshalovich, 1975), example Ä´=1/2 ψk ¶/¶ψk. Further, for the state of class 2j, operator Ä´ will be replaced by j everywhere. The operators Q for Ψ of class 2j have the form:
Q(3)1=i j cosφ sinθ+i cosφ cosθ ¶/¶θ–i sinφ/sinθ ¶/¶φ+i sinφ ctgθ ¶/¶γ.
Q(3)2=ijsinφ sinθ+icosφ sinθ ¶/¶θ+i cosφ/sinθ ¶/¶φ–icosφ ctgθ ¶/¶γ.
Q(3)3=ij cosθ–i sinθ ¶/¶θ.
Q(1)2=ijcosφ sinγ+ijcosθ sinφ cosγ-isinφ sinγ ¶/¶φ+icosφ cosγ ¶/¶γ-i sinφ cosγ sinθ ¶/¶θ.
Q(1)1=-ij sinφ sinγ+ij cosθ cosφ cosγ-i sinθ cosφ cosγ ¶/¶θ-i cosφ sinγ ¶/¶φ-i sinφ cosγ ¶/¶γ.
Q(1)3=-ijsinθ cosγ–isinγ ctgθ ¶/¶φ-icosγ cosθ ¶/¶θ + isinγ/sinθ ¶/¶γ.
Q(2)1=-ijcosγ sinφ-ijcosθsinγ cosφ+i sinφ sinγ ¶/¶γ–icosφ cosγ ¶/¶φ+ i sinγ cosφ sinθ ¶/¶θ.
Q(2)3=ij sinγ sinθ+icosγ sinθ ¶/¶θ+icosγ/sinθ ¶/¶γ-icosγ ctgθ ¶/¶φ.
Q(2)2=ij cosφ cosγ–ijcosθ sinφ sinγ+isinθ sinφ sinγ ¶/¶θ-icosφ sinγ ¶/¶γ-i sinφ cosγ ¶/¶φ.
Under the action of the operator J,Q with upper and lower indices +, - and 0 on Djm,m' the indices m, m' can increase, decrease or remain unchanged (Sventkovsky, 2004). Substituting the expression for Q(p), J we can verify that Q(p), J have the same Lie algebra (7) as the Lie algebra of the Lorentz group (Equation 5), where p=1,2,3 corresponded to tree angular presentations (the spinor, tensor presentations) of the Lorentz group, that is,
[Ji, Jn]=ieink Jk, [Q(p)i , Jn]=ieink Q(p)k ,[Q(p)i ,Q(p)n ]=-ieink Jk. (7)
The Lorentz transformation v=|v|x3 with the (boost) generator Q(3)3 , p=3 is independent of φ and γ and is symmetrical with respect to two observers X3 and X(3), hence φ'=φ, γ' =γ , th(χ)=v/c (13).
The Lorenz transformations in Minkowski space and in the space of orientations respectively of four-dimensional vectors A,A0 and X(3),X(0)0 , bivectors E, H and X(1), X(2),as well as spinors C and y=ξ(±j) are opposite, inverse to each other, but the transformations of the vectors under the spatial rotation are the same. This ensures fulfillment of Sommerfeld condition about Lorentz invariance:
YA = AX(3) + A0 X(0)0 c
YEH=EX(1)+HX(2), Y=yC.
The Lorentz transformation for angular variables which was obtained earlier directly follows from the Lorentz transformations of spinors:
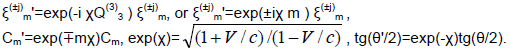
These transformations of angles correspond to the known transformation of angles for polarized light with direction velocity along the axis X(3) and velocity v'=-v, (Pauli, 1958). The Casimir operators of the Lorentz group in angular representations are operators J2-Q(3)2, J,Q(3) have been obtained from the Casimir operators K2-L2,LK of the Lorenz group by replacing the generators of the Lorentz group L,K by J,Q(3). The irreducible representations of the Lorentz group are characterized by a pair of numbers corresponding to the eigenvalues of the operators Z2± where Z±=(J ± iQ(3))/2, [Z± Z±]=iZ±, [Z+Z-]=0. The spinors ξ(j), ξ(-j) are transformed, respectively on irreducible representation (j,0) and (0,j), because Z2+ξ(j)=j(j+1) ξ(j), Z2-ξ(j)=0, Jk ξ(±j)=ξ(±j) Sk, Q(3)ξ(±j)=±i ξ(±j) S.
The matrix representations of these two-irreducible spinor representation of the Lorentz group for an arbitrary j can be obtained from (7), p=3 by replacing the operators Jk,Q(3)k on their matrix representations in the spinor basis j, ψ=ξ(j)Tor ψ=ξ(j)T, as <ψT|Q(3)k|ψ>. The elements of ξ(±j)m whose Lorenz transformation has no an additional component are the eigenfunctions of Q(3)3.
Q(33ξ(±j)m=±im ξ(±j)m, J3ξ(±j)m=m ξ(±j)m
The bivectors X(-),X(+) are transformed respectively on irreducible representations (1, 0) and (0, 1) of the Lorentz group, because Z(±)2X(-)=X(-)(1±1). The four-vector X(3) and X(0)0 is transformed on irreducible representation (1/2, 1/2), because Z(±)2X(3)=3/4X(3). Thus, the representation of the Lorentz group (Equation 7) for the class 2 in 10-dimensional basis ψ=X(i)n splits into irreducible vector representations for the basis X(3) and X(0)0 and into adjoint representation for the real basis X(1) and X(2).
Definitions
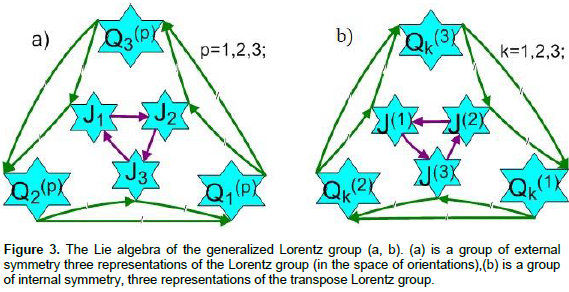
The Generalized Lorentz group (Equations 1, 7 and 8) is the group consists of 16 generators Ä´, Jn, J(k) and Q(n)k which was obtained by combining the known angular representation of the Lorentz group (Equation 7) (Sventkovsky, 2004) and its transposed angular representation.
[Q(n)i ,Q(p)k ]=iδik enpm J(m)-i δnp eikn Jn, [Q(i)p, J(n) ]=ieink Q(k)p (8)
The generalized group provides symmetry between the representation and transpose representation of the group or between the vector rotations of the original local observer and the isovector rotations of the rotated local observer, it is illustrated in Figure 3. The symmetry operator W retains the invariance of the Lie algebra of the generalized Lorentz group Q(n)k=(-1)(k+n) W Q(k)n. Matrix representations of the generators of the generalized Lorentz group (Equations 1, 7 and 8) in the basis bi-spinor, j=1/2 corresponding the replacement of Jn, J(k),Q(n)k , Ä´ by S(0)n , S(k), S(0)k S(n), j matches 16 basis elements of the full Clifford algebra formed from Dirac’s gamma matrices (Fluge, 1974). The proof uses identities:
Jn ψ = ψ S(0)n , J(k) ψ = ψ S(k), [S(k), S(n)]=-i eknp S(p),
Q(n)k ψ=2i J(n)Jk ψ=ψ 2iS(n)S(0)k , 2J(3)ψ =ψ g4, 2J(1)ψ=ψ g0,
2J(2)ψ=ψ Ä0, 2Q(2)ψ =ψ g, 2Q(1)ψ =ψ Ä, <ψT |Jk|ψ>=S(0)k
Where g0, g and Ä0, Ä-gamma Dirac matrices in the Weyl basis:
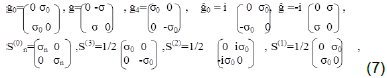
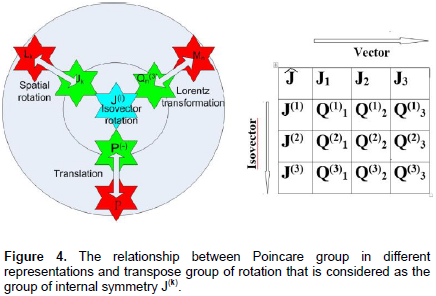
The infinitesimal generator of the Lorentz group Lk and Kn (Ohnuki, 1988) are identical to matrices <ψT|Jk| ψ>, <ψT |Q(3)n | ψ>by using the basis ψ=(X(0)0,X(3)1 X(3)2 X(3)3). This can be easily checked using (13). The study can also verify that ten generators of the Poincare group in angular (spinor) representation J, Q(3), Q(-), i J(-), for p=3, which were obtained using the generators of the generalized Lorentz group, have the same Lie algebra (Equations 5 and 6) of the ten generators of the Poincare group L,K,P and P0, where Q(-)=Q(1)+i Q(2). Four-dimensional vector (P(-), P(-)0 )=(Q(-), i J(-)) can be regarded as analogous to the momentum operator in the Lie algebra of angular variables, since they have the same Lie algebra as Poincare group. It is illustrated in Figure 4. The study can also verify using the Baker-Campbell-Hausdorff formula that generators of the Poincare group in angular representation have the known transformation properties under the Lorentz transformation, (J,Q(3)) transformed as bivector, (Q(-), iJ(-)) transforms as four-vector momentum, J(3) transform as scalar. Generalized Lorentz group is realized in the space of orientations. The Pauli-Lubanski vector in the operator angular representation has the equivalent form Å´0=(PJ), Å´=P0J-[PQ(3)] that is obtained from Pauli-Lubanski vector by replacing the matrices L and M by the operators J,Q(3). The operators Å´0 and Å´ in the matrix representation J,Q(3) in the corresponding basis is identical to the original Pauli-Lubanski vector. The second Casimir operator of the Poincare group for the seven-dimsenional space has the equivalent form (Å´02-Å´2) that is obtained from the second Casimir operators by replacing the Pauli-Lubanski vector by Pauli-Lubanski vector in angular representation.
The generalized Dirac, Maxwell, Weyl equations
The operator part of the Poincare invariant equations for the wave function which has the momentum operators in the first degree are invited to express in symmetric form an equal to the scalar product of two four-dimensional vectors of the momentum operators for space-time and for space of the orientations. We have: N(±)=P(±)P-P(±)0 P0 where N( )=N(1) ± i N(2) is complexified operator, below used real invariant operators:
N(1)=Q(1)P+J(2)P0/c, N(2)=Q(2)P-J(1)P0/c.
Thus Poincare invariant equations for the wave function can consist of two equations have different spatial parities corresponding to an even operator:
N(1)=ṔΠN(1) and an odd operator N(2)=-á¹”ÎN(2). These equations will be referred to as the generalized Dirac,
Maxwell, Weyl equations. The generalized Maxwell equations for the class 2j=2, describing the spinless state and its analogue have the form (Equations 9 and 10):
Ψ=EX(1)+HX(2), < Ψ|Ji|Ψ>=0, < Ψ |J(k)| Ψ >=0
N(1) Ψ =4π ΨC (9)
N(2) Ψ =0. (10)
where ΨC=IX(3)+I0 cX(0)0 , I=(I1, I2, I3) is vector density of electric current , I0 is the density of the electric charge. Representation of generalized Maxwell Equations (9) and (10) in the basis X(k)n are equivalent to the Maxwell equations
[PH]+P0E/c=-i4π/c I, (PE)=-i4 π I0, (11)
[PE]-P0H/c=0, (PH)=0. (12)
For proof, we substitute in (9.10) the form Ψ, N(1) and N(2 and use identity:
J(i)X(n)p=-ieinkX(k)p, Q(n)k X(0)0=ij X(n)k, (13)
Ji X(p)n=ieink X(p)k , Q(m)i X(p)n=iδi,nδm,pX(0)0+ieinkempd X(d)k.
(Q(1)P+J(2)P0/c)Ψ=(i[PH]+iP0E/c)X(3)+i(PE)X(0)0=4π(IX(3)+I0X(0)0 ). (Q(2)P-J(1)P0/c) Ψ=(-i[PE]+iP0H/c)X(3)+i(PH)X(0)0=0.
Equating to zero the coefficients in Equation 9 and 10 at each of the bases X(3)k and X(0)0 , we obtained, respectively, a second (Equation 11) and a first pair of Maxwell’s equations (Equation 12). The normalization of the wave function in the double space of orientations (over the angles) at the point x1, x2, x3, is equal to the energy density of the electromagnetic field: b2<ΨEH |ΨEH>/(8 π)==(E2+H2)/(8 π).
The Poynting vector are written in the form:
-i c b2<ΨEH|Q(3)| ΨEH>/(8 π)=c[EH]/(4π),
The generalized Dirac equation j=1/2,1, 3/2 , . . . have the form (Equations 14 or 15). Representation (Equations 14 or 15) in the basis, j=1/2, (2) coincide respectively with the ordinary Dirac equations (Equations 16) for the electron Ψ=ψ C or with the Dirac equations (Equation 17) for the unknown particles Ψ^=ψ Ĉ, me is the mass.
N(2) Ψ=mec/(2h) Ψ (14)
N(1) Ψ^=mec/(2h) Ψ^ (15)
For proof, we substitute in (Equations 14 and 15) the form of N(1), N(2) , ψ=(ψ1, ψ2, ψ3, ψ4), (2). and using the identities N(2)ψ=ψ (g P-g0 P0/c), 2N(1)ψ=ψ(Ä P-Ä0 P0/c). Equating to zero the coefficients at each from the bases ψk in (Equations 14 and 15), identically we obtain equation Dirac in chiral representation with matrices, respectively g, g0 (Ryder, 1987), (16) and Ä, Ä0, (Ryder, 1987):
(g P-g0 P0/c+mec/h) C=0. (16)
(Ä P-Ä 0 P0/c+mec/h) Ĉ=0. (17)
The spinor Lorentz transformation of the N(2) when using a basis ψ=(ψ1, ψ2, ψ3, ψ4) corresponds to the transformation group SL(2, С), relativistic spin group:
ψ'=ψU, U-1<(ψ*T N(2) ψ) >U=U-1 (gP-g0/c P0) U , ψ=(x(1/2)T, x(-1/2)T)
U-1 (g P-g0/c P0) U=g P'-g0/c P'0 ,
U-1= U*T space rotation, ξ(±1/2)m'=exp(±m χ) ξ(±1/2)m for Lorentz rotation. Solution of these Equations 14 and 15 for a particle at rest, assuming that the term with the momentum operator
P vanish, correspond to standard representation of basis and has the form:
-J(1)P0/c Ψ=mec/(2h) Ψ, J(1)Ψ= Ψ/2 (18)
J(2)P0/c Ψ^=mec/(2h) Ψ^, J(2)Ψ^=± Ψ^/2 (19)
Decisions have a zero balance between left and right
Ψ=C(ξ(1/2) ξ(-1/2)), Ψ^=Ĉ (ξ(1/2)±i ξ(-1/2)),
<Ψ|J(3)|Ψ>=0,<Ψ^|J(3)|Ψ^>=0.
At the inner inversion, electron becomes the positron (Equations 16, 18 and 20) and on the contrary, but the unknown particle remains unknown particle (Equation 17, 19 and 21):
Î (ξ(1/2) ξ(-1/2)) =±(ξ(1/2) ξ(-1/2)) (20)
Î (ξ(1/2)±i ξ(-1/2))=±i(ξ(1/2)±i ξ(-1/2)) (21)
Generalized Weyl equation with spin j=1/2 for Lorentz invariant Ψ(±)=C(±) ξ((±1/2) is identical to the Weyl equation (Akhiezer and Berestetskii, 1965), for right or left neutrinos, have view:
N(±) Ψ( )=0, or, (-P0c ± P σ) C(±)=0. (22)
Balance for the state Ψ(±) between left and right violated, as J(3)Ψ(±)=±Ψ(±)/2.
Theorem 2
Mirror symmetry of basis states with spin j=1/2. The mirror basis μ(±1/2)=ξ((1/2) i ξ((-1/2)is unique. No other bases with this property exist. This basis is not changes under the inversion Î μ(±1/2)=±i μ(±1/2). The proof follows from the completeness set of the basis and the choice of a basis in the form of linear combinations of basis ξ((1/2) and ξ((-1/2).
Theorem 3
Mirror antisymmetry of basis states with spin 1/2. There is a subgroup of transformations η(1/2)=cos(β/2) ξ(1/2)-sin(β/2) ξ(-1/2), η(-1/2)=sin(β/2) ξ(1/2)+cos(β/2) ξ(-1/2) for any β, when the bases are transformed into each other under inversion Îη(±1/2)=±η(( 1/2). The proof is similar. Thus, there is a plurality of bases having mirror antisymmetry property η(±1/2), but there is only one basis with mirror symmetry property μ(±1/2). It is additionally assumed that particles in rest with a nonzero mass have a zero balance between the left and the right<η(±1/2)|J(3)|η(±1/2)>=0 which is implemented for β=π/2. The symmetry of Maxwell’s equations when (E,H) is replaced by (-H,E) is called the electromagnetic duality. In general, there is a Heaviside-Larmor-Raynicha subgroup (HLR) (Konopelchenko, 1977):
E'=E cos(α)+H sin(α), H'=-E sin(α)+H cos(α ).
These transformations correspond to the turn of the rotated local observer about axis X(3) by angle α or to Ψ'=exp(iα J(3)) Ψ, γ'=γ+α in the framework transformations of generalized Lorentz group. Example, the use of the invariance of Ψ'=Ψ and Ψ=EX(1)+HX(2), α=π/2, X(1)(γ)=-X(2)(γ+π/2), X(2)(γ)=X(1)(γ+π/2) are obtained conversio
In the isotropic Minkowski space, the multicomponent wave function Ck |k> corresponding to the spin, vector states equivalently is described by a one-component wave function Ck ψk that depends on the position x1, x2, x3, t and the orientation φ, θ, γ of the local rotated observer. This corresponds to the replacement of the matrix basis | k> by an operator basis ψk, that depends only on φ, θ, γ with the same transformation properties as for the matrix basis. φ, θ, γ may be interpreted as the possible orientation of the particle. Any angular dimensions (not are tied) does not depend on a specific spatial point since they are the same for all points of the space x1, x2 and x3. For a unified description of states with spin j, vector and tensor fields dependent on the orientation of the meter, a state of a class 2j was introduced as a class of functions Ψ =ψ C which may be represented by a homogeneous polynomial of degree 2j of D(1/2)m, m'. The known difficulties associated with the ambiguity of the transformations under the imbedding of a new space into the Minkowski space (Cartan, 1927) were successfully overcome by considering a well-known class of functions 2j, (describing spinors, tensors) invariant under the Lorentz transformation and after determining the operators of the Poincare group for it in the angular representation. The Lorentz group in matric representation was essentially expanded to the generalized Lorentz group due to the inclusion in it of transposed representations the Lorentz group, namely: Generators of two well-known groups in the angular representation corresponding to the rotation group SU(2), Jn and the transposed rotation group SU(2), J(k) and also the generators of the Lorentz group Q(p) for different angular representations p=1,2 and 3 form a generalized Lorentz group.
The symmetry of the generalized Lorentz group consists in its invariance with respect to the transpose operation in the matrix representation (or under the action of the operator W) and corresponds to the symmetry between the original observer and the rotated local observer. The generalized Lorentz group besides transformations associated with the Lorentz group has an additional degree of freedom which can be considered as the transformations of internal symmetry. If the operators of the group Q(p), J are in correspondence with the operators of the group K, L in the Lorentz transformation, then the operators J(k) in the generalized group do not have such correspondence, J(k) can be regarded as a generator group of the internal symmetry of particles, fields, Ψ (Figure 4). The spin projection and the directions of the vector field are invariant under transformation by means of J(k). Spinors and vectors are always transformed into spinors and vectors under transformations J(k). The generalized Lorentz group in the angular representation has been obtained by combining the internal symmetry group J(k) and the group of external symmetry with generators Q(p) and J corresponding to the Lorentz group in the angular representation. Inversion of space is always accompanied by a corresponding transformation of internal dimensions. Internal inversion: Transformation of Y in the mirror state can be obtained via (continuous) rotation using the generator J(k) within the framework of transformations of the generalized group that preserve the invariance of the Lie algebra of the Lorentz group in angular representation. Therefore, the generalized Lorentz group, when spinors and vectors are transformed, includes the full Lorentz group. This fact partly explains that the parameter space for the SU(2) and SO(3) are different from each other twice.
Main laws nature equation of Dirac, Maxwell is like clockwork. All objects, wave function are moved, are transformed only with using generators of group, but do not move themselves. All objects can be moved over short distances with almost no distortion, but only objects that are eigenfunctions of generators (generalized) group. Figure 5 can be moved with the help of those generators without distortion on any distances. For example there is an identity: exp(iaPn) exp(ikxn)=exp(ik (xn+a)). To obtain the first-degree equation on momentum, Dirac introduced a four-dimensional vector (from gamma matrices) independent of the coordinates. Similarly the article introduces a four-dimensional vector P(+)k from the new angular dimensions that do not depend from the coordinates of space-time. The simplest equations of nature must be first-degree differential equations with respect to dimensions and to be Poincare invariant. For this purpose it is advisable to use the Casimir operator Pk and Pk of the Poincare group in which one of the two momentum operators is replaced by the momentum operator in the angular representation which is unique for p=3. As a result two real Lorentz invariants N(1), N(2), Pk P(+)k=N(1)-i N(2) have been obtained. These operators correspond to the first Casimir operators for the seven-dimensional space and have been used to obtain Dirac, Maxwell, Weyl equations. The matrices, bases were equivalently replaced by operators, basis functions with the same transformation properties, when introducing angular dimensions.
The generators of the Poincare group in the angular representation have been used to obtain the Dirac matrices and the resulting matrix at the momentum operator in the matrix form of Maxwell’s equations. Generalized equation Dirac and Maxwell have two forms of representation N(1), N(2) which correspond to different parity at the spatial inversion. There are good reasons to believe that there are no other Poincare invariants except the first Casimir operator that are linear with respect to momentum operators. The Lorentz invariants N(1), N(2) allow to write the equations of Dirac and Maxwell in a uniform form for the states of class 2j=1, 2 and to generalize these equations for any j. The quantization of the electric, magnetic charge can be regarded as the quantization of the analogue of the spin J(1), J(2), (18), namely. Generalized Dirac equation for spin 1/2 in the form N(2),(14) in the matrix representation is identical to the Dirac equation for electron, positron and has a solution for a particle at rest, corresponding to a state with a mirror antisymmetry and has the projection J(1) Y=-Y/2 for electron, J(1) Y=Y/2 for positron. Scalar, Lorentz invariant has the form:
Cg0CT=<Y|J(1)|Y>=<Y'|J(1)|Y'>.
Generalized Dirac equation for spin 1/2 in the form N(1), (Equation 15) in the matrix representation is identical to the Dirac equation with matrices g, g0 with corresponding to of Clifford algebra has a solution for a particle at rest, corresponding to a state with a mirror symmetry, and has the projections J(2) Y=±Y/2, which was named as unknown particle. Pseudo scalar Lorentz invariant, (Jante and Schroers, 2016) has the form:
Cg0g4CT=<Y|J(2)|Y>=<Y'|J(2)|Y'>.
Generalized Weyl equation for spin 1/2 in the form N(±), (Jante and Schroers, 2016) is identical in the matrix representation to the Weyl equation for neutrino, anti-neutrino and has a solution Y, corresponding to a state with the projections J(3) Y=±Y/2. Since Y=ψk, (2) is also the eigenfunctions of the Q(3)3 and therefore Y does not change shape when the Lorentz transformation. This situation corresponds to a particle moving with the speed of light along x3 and which may be either right or left, J(3) Y(-)=-1/2Y(-), Y(-)=ψ3 correspond antineutrinos J(3) Y(+)=½ Y(+), Y(+)=-ψ2-neutrinos. Generalized Maxwell equations for class 2j=2 in the form N(1), (Equation 9) and N(2), (Equation 10) in the matrix representations identical respectively the second pair of Maxwell’s equations for electrical charge (Equation 11) and the first pair of Maxwell’s equations for magnetic charge equal zero (Equation 12).
It should be noted that generalized Maxwell’s equations (Equations 11 and 12) describe state YEH without spin. Principle of superposition of states always performed for states of class 2j in each point and for each orientation φ, θ and γ. The existence of the additional property of principle of superposition of states for the class 2j=1, 2 have been revealed in this paper. This property will be named to the property unchangeability (same) functional dependence wave function (analog of form) of the angular dimensions when states are added. It was found that for spin states j=1/2 there are only two types of independent forms ψ1, ψ4 and for class 2j=2 there are three types of independent forms X(p)3 that corresponds different to vector fields. In accordance with the decisions of generalized Dirac equation, Weyl in nature can only be implemented in three types of point particles for spin 1/2, which are classified according to different types of symmetry and correspond with the three projections of analogue of the spin 1/2, J(k) Ψ=±Ψ/2 respectively for electron at rest, for monopole at rest, for neutrino at flying. A particle and its antiparticle differ a sign of projection J(k). Taking into account that the solutions of the generalized equations, basis states correspond to eigenfunctions of generators of the generalized Lorentz group from φ, θ and γ, it can be concluded next: In nature for spin (vector) states is realized do not just Lorentz group, but generalized an Lorentz group. So some physical systems can be represented more accurately by using a generalized group Lorentz.
The determining role of the generators of the generalized Lorentz group in the formation of the Dirac, Maxwell, and Weyl equations (matrices for the momentum operators (Dirac matrix) and also of irreducible representations of the Lorentz group are shown. A number of known transformations, such as inversion, Heaviside-Larmor-Raynich, charge conjugation, transition to different representations were equivalently unified and represented using the transformations of the group J(k) within the framework of transformations of the generalized Lorentz group. The superconductivity is proposed to be considered as a manifestation of the additional degree of freedom associated with the transformations of the generalized Lorentz group. The generalized Lorentz group in the matrix representation exists regardless of the use or non-use of angular variables. Three bases of the class 2j=2, ψ=X(+),X(-), (X(3),X(0)0) correspond to three irreducible representations of the Lorentz group (1, 0, 0, 1, 1/2, 1/2) and have three Lorentz invariant of Ψ. The existence of three Lorenz invariants Ψ(±)=F( )X(±),ΨEH+ΨA/Λ for the electromagnetic field E,H, A,A0 leaves the possibility of a transition from one state of Ψ to another in the framework of the transformations of the generalized Lorentz group and which are composed from linear combination of this three Lorenz invariants. One and the same electromagnetic field corresponding to the Maxwell equations, can correspond to different Ψ(±)=F( ) X(±) or Ψ=ΨEH. The Lorentz invariants ΨEH, ΨA cannot describe state with spin, chirality, for example of photon, but Ψ(±) can, as b2<Ψ(±)|J|Ψ(±)|>=±4[EH] is the direction and value of spin. Given the above, the following mechanism for the transition of a conductor to superconducting state proposed. The low-temperature superconductivity corresponds to a spontaneous transition to spinless state: Ψ=ΨEH+ΨA/Λ.
The high-temperature superconductivity (in iron-based materials) can correspond to a spontaneous transition to left (right) state Ψ(±), that correspond to chiral superconductors J(3)Ψ(±)=±Ψ(±). The observed difference between left and right chiral superconductivity (Zyga, 2017), when a magnetic field is applied parallel to a superconducting chiral nanotube, electric signals travel in one direction only, can be explained by the existence of a spin of the electromagnetic field proportional to the Poynting vector but differently directed for the left and the right states. Taking advantage of the fundamental provisions of the theory of groups, whereby the result of operations on one class 2j=2 automatically transferred to the result of the same operations on another class 2j=1 of the same group, has been offered the following axiom: The transformation γ'=γ+π/2 leads to an exchange of forms N(1) and N(2) in generalized Dirac equation and in generalized Maxwell equations, formally leads to the same results, namely: Since generalized Maxwell’s equation for a particle of class 2j=2 with the electric charge is transformed into generalized Maxwell’s equation for particles with a magnetic charge. Matrix representation of this equitation in the basis X(n)k ,X(0)0 coincide with corresponding the equations Maxwell, consequently generalized Dirac equation of class 2j=1 for an electron is transformed into generalized Dirac equation for the Dirac monopole. Matrix representation of this equation in the basis j=1/2, bispinors, (2), also coincide with corresponding the Dirac equations. From the (generalized) equation it follows that is an unknown particle has a mirror symmetry for and coincide with Dirac monopole. The difference between an electron and the Dirac monopole is difference in types of mirror symmetry, a monopole is a mirror particle and an electron has a mirror antisymmetry.
The possibility of the existence of the Dirac monopole is determined by the possibility of the existence of a mirror particle. The Dirac monopole in a state of rest with spin 1/2 has a unique basis with mirror symmetry, that is, it does not change under the inversion, but there are a lot of bases state of spin 1/2, with mirror antisymmetry (the particle passes into the antiparticle). This circumstance, which need to explore and the possible can dramatically reduce the likelihood of the occurrence of such particles (the Dirac monopole), when there is a transition to a unique basic state down to zero. The subspace of angular dimension plays an important role in the formation of the basic laws of nature. The basic operator N(±) is an analog of the Casimir operator and is written in a symmetric form with respect to the coordinate space and the double orientation space as products of the momentum operators for each spaces. The existence only of three different (angular, spinor) purely complex representations of the Lorentz group simultaneously in the framework of the generalized Lorentz group can be considered as a justification for the existence of three generations of leptons (electrons, muons, tau-leptons). The existence only of three different (angular) purely complex representations of the transpose Lorentz group (as shown in Figure 3) simultaneously in the framework of the generalized Lorentz group can be considered as a justification for the existence of three color charge of quarks. According to group theory, the result does not depend on the form of the representation. Because, in some cases, compared with the standard matrix approach, the use of operators from angular dimensions has a more obvious physical interpretation, simplicity and generality representation for any j.
The authors have not declared any conflict of interests.
The author extends his thanks to Candidate of Physical and Mathematical Sciences Bolokhov Sergey for discussions and valuable remarks.
REFERENCES
|
Akhiezer AI, Berestetskii VB (1965). Quantum electrodynamics. Interscience Publishers John Wiley and Sons, Inc., New York, London, Sydney.
|
|
|
|
Bidenhander LC, Lauk JD (1984). Angular momentum in quantum physics. Moskva. M. Mir 1:34-137.
|
|
|
|
|
Cartan E (1927). Sur la possibilit de plonger un espace riemannien donn dans un espace euclidien. Annales de la Société Polonaise de Mathématique 6(1).
|
|
|
|
|
Casimir HBR (1931). Rotation of a rigid body in quantum mechanics.
View
|
|
|
|
|
Fluge S (1974). Practical Quantum Mechanics. Springer, New York. Mir Moscow pp. 186-217.
|
|
|
|
|
Jante R, Schroers BJ (2016). Taub-NUT dynamics with a magnetic field. Journal of Geometry and Physics, pp. 104:309.
|
|
|
|
|
Konopelchenko BG (1977). Symmetry groups in quantum field theory. Physics of Elementary Particles and Atomic Nuclei 8(1).
|
|
|
|
|
Ohnuki Y (1988). Unitary representations of the Poincare group and relativistic wave equations. Word Scientific Pub. Co. Inc.
View
Crossref
|
|
|
|
|
Pauli W (1958). Theory of relativity. Pergamon press London.
|
|
|
|
|
Portnov YA (2011). Gravitational interaction in seven-dimensional space-time. Gravitation and Cosmology, 17:152-160.
Crossref
|
|
|
|
|
Ryder L (1987). Quantum Field Theory. M. Mir 57.
View
|
|
|
|
|
Sventkovsky RA (2004). Angular symmetry of spacetime and the spinor representation of Poincare group. International Journal of Physical Sciences 9(9):213-223.
|
|
|
|
|
Teschl G (2009). Mathematical methods in quantum mechanics: With applications to Schrodinger operations. American Mathematical Society, pp. 173-179.
Crossref
|
|
|
|
|
Varshalovich DA (1975). Quantum theory of angular moment. English edition of the original Russian publication Nauka, Leningrad. pp. 64-67.
|
|
|
|
|
Zyga L (2017). Chiral superconductivity experimentally demonstrated for the first time. Phys.org.
View
|
|
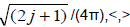/(4π),<,> icons are used only for the orientations space, and δi,k is the Kronecker delta, δk,k=1. Any column ξ(m') of the matrix D(j)* is transformed in the same manner as a spinor j under spatial rotation and corresponds to a complete set of basis vectors describing states with spin j, (Varshalovich, 1975), as Jξ(m')T=ξ(m')TS, [Si,Sn]=ieink Sk, Si is the matrix operator of angular momentum. The rotated observer for state j also as original observer has 2j+1 degrees of freedom corresponding to the analog of the spin projections m'=-j..,+j,
