ABSTRACT
The total and partial mass attenuation coefficients for different Maraging steel compositions have been determined by using the WinXCom and MCNP5 programs. The effective atomic number, Zeff, and effective electron number, Neff, for the studied steels have been determined via the total mass attenuation coefficients μ/ρ, the total atomic and electronic cross sections (σa and σe) of the investigated steels. The shielding parameters μ/ρ, Zeff, and Neff have been calculated at the incident photon energy range of 1 keV–100 MeV. The calculated results of total and partial mass attenuation coefficients, the effective atomic number and the effective electron number by using MCNP5 program were found to be in good agreement with the theoretical results of the WinXCom program. The calculated data clarify that the different steel compositions under investigation have so far the same ability of gamma attenuation. Also, it was found that the total mass attenuation coefficients of the different investigated steels (cobalt free-Maraging steels) are comparable to the C250 standard steel (cobalt Maraging steel).
Key words: Gamma rays, shielding, mass attenuation coefficients, effective atomic number, effective electron number.
Steels are used in the reactor core, fuel transport and storage, plant structures and a lot of other nuclear uses. The ultra-high strength of the most expensive Maraging steels is due to the precipitation of inter-metallic compounds (cobalt, nickel and molybdenum) during the aging process. Due to the sharp increase in the cobalt price, the development of a family of cobalt free Maraging steel is promoted. Titanium can be used as the primary strengthening element, replacing cobalt in steels (Vasudevan et al., 1990; Sha et al., 1993). On the other hand, chromium was added to increase the corrosion resistance of the proposed steels. The previous are the ,causes of porn new Maraging steel with different mechanical and technological properties. As a result of use on a large scale in the nuclear field (nuclear power plants such as fusion reactor, accelerator driven systems or the fission generation reactors) Maraging steels should be investigate as a shielding material. In order to achieve this purpose the radiation absorption mechanism in materials should be known. This can be represented by some physical parameters such as mass attenuation coefficients μ/ρ, effective atomic number Zeff and effective electron number Neff. Several investigators (Han and Demir, 2009a, 2009b; Baltas et al., 2007; Baltas and Cevik, 2008; Celik et al., 2008; Manjunathaguru and Umesh, 2007; Manohara et al., 2008a, 2008b, 2009a, 2009b, 2010; Manohara and Hanagodimath, 2007a, 2007b; Singh et al., 2008; Taylor et al., 2008; Gounhalli et al., 2012a; Sidhu et al., 2012; Gounhalli et al., 2012b; Kurudirek, 2014; Un and Sahin, 2011, 2012; Akkurt, 2009; Limkitjaroenporn et al., 2013; Medhat and Wang, 2015; Elmahroug et al., 2015; Un and Caner, 2014) have made extensive studies for these shielding parameters in a variety of composite materials such as biologically important materials, semiconductor, alloys, dosimetric compounds, glasses, drugs, and explosives. The mass attenuation coefficient μ/ρ (cm2/g) is a measure of the probability of interactions of photon with matter (Hubbell, 1982, 1999; Hubbell and Seltzer, 1995). This coefficient is not constant but depends on the energy of the incident photon, and the density and atomic number of elements. For compound and mixtures, it depends on the effective atomic number Zeff and effective electron number Neff. However, as originally stated by Hine (Hine, 1952) the effective atomic number Zeff of a multi-element material is not a constant, it varies with the energy of the incident photon.
The advent of powerful processors and computer architectures since the early 1990’s made possible the increasingly important utilization of Monte Carlo simulation programs to model complex systems, both from the point of view of the physics (type of particles and interactions, energy ranges, etc.) and from the point of view of a detailed geometrical description (Vaz, 2009). Wherefore, Monte Carlo simulations has rapidly increased in the scientific field, with applications such as radiation shielding optimization, component effects, support of scientific studies, and analysis of biological effects. The well-known WinXCom program is usually employed for calculating X-ray and gamma-ray attenuation coefficient and interaction cross sections of different materials (El-Khayatt et. al., 2014). The aim of this study is to provide available information concerning using this kind of steel as a gamma shielding in nuclear applications. So, WinXCom and MCNP5 programs were used to calculate the partial and total mass attenuation coefficients for different compositions of Maraging steels at photon energies (1 keV–100 MeV). The attenuation coefficient data were then used to obtain the effective atomic numbers Zeff and the effective electron number Neff of the investigated materials.
A parallel beam of monoenergetic gamma-ray photons is attenuated in the matter, according to the Lambert-Beer exponential equation
where and are the transmitted and the incident beam intensity of photons, respectively, t and ρ are the material thickness and density, respectively, and μ/ρ is the mass attenuation coefficient.
For compound or mixture, the mass attenuation coefficient can be obtained from the coefficients of the constituent elements which are assumed to be additive to the weighted average
where and are the fractional weight and the mass attenuation coefficient of the ith constituent element, respectively. This mixture rule is valid with the assumption that the effects of molecular binding and the chemical and crystalline environment are negligible.
Using the total mass attenuation coefficients of a material, the total atomic cross-section, σa, can be evaluated by the following relation (Manohara et al., 2008a, 2008b; Akkurt, 2009; Elmahroug et al., 2015; Akkurt and El-Khayatt, 2013b; Gowda et al., 2004, 2005; Içelli et. al., 2011; Prasad et al., 1998)
where NA is the Avogadro’s number, Ai is the atomic weight of the ith constituent element of the material.
Also, the total electronic cross-section, σe, can be obtained by the following formula (Manohara et al., 2008a, 2008b; Akkurt, 2009; Elmahroug et al., 2015; Akkurt and El-Khayatt, 2013b; Gowda et. al., 2004, 2005; Içelli et. al., 2011)
Where fi is the fractional abundance (the number of atoms of element i relative to the total number of atoms of all elements in the mixture), Zi is the atomic number of the ith element in a mixture.
The effective atomic number Zeff can be obtained from the ratio between the total atomic effective cross-section and the total electronic effective cross-section as the following equation (Manohara et al., 2008a, 2008b; Akkurt, 2009; Elmahroug et al., 2015; Akkurt and El-Khayatt, 2013b; Gowda et al., 2004, 2005; Içelli et al., 2011; Kaur et al., 2000)
The effective electron number (Neff) (the electrons number per unit mass, electron/g) can be calculated from the following equation (Manohara et al., 2008a, 2008b; Akkurt, 2009; Elmahroug et al., 2015; Akkurt and El-Khayatt, 2013b; Gowda et al., 2004, 2005; Içelli et al., 2011)
The relation between Neff and Zeff can be deduced from replacing the value of from Equation (3) in Equation (6) as the following
equation
PROCEDURE OF THE INVESTIGATED STEEL
Production
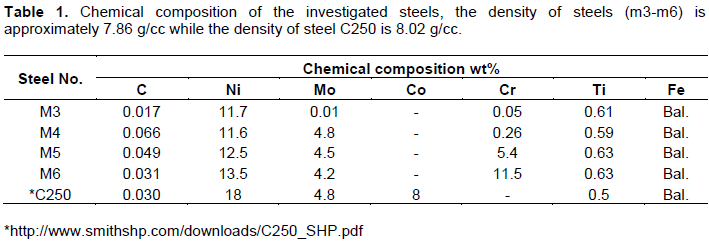
Five kilograms of each of tested Maraging alloys were melted from pure elements in vacuum arc melting furnace with non-consumable tungsten electrode and water cooled copper crucibles. Before melting, to minimize interstitial gases including oxygen and nitrogen from the furnace atmosphere, titanium getters were melted, and high purity argon was used as an inert gas. On the other hand, in this approach used materials were heated to 600°C to ensure water and crystalline water removing. New and developed batch of Maraging was loaded into the vacuum arc melting furnace with non-consumable tungsten electrode crucible under vacuum with pressure 1 × 10−3 mbar. The furnace was energized noting the power (based on voltage, current, and time in each setting) required for melting. To ensure homogeneity of the produced steel ingots, the produced steel ingots were melted twice, inverting the ingot after each melting. The chemical composition of produced steels was determined using spectrographic (SPGA). Metal forming and heat treatment of tested steels were reported elsewhere (Hossam et al., 2010; Halfa and Reda, 2015). Well prepared and polished steel ingots were optically examined using Axiovert 40 MAT, Carl Zeiss, Switzerland microscopy after chemical etching in the solution of 1 g CuCl2/30 ml HCl/50 ml HNO3/100 ml H2O (Hossam et al., 2010; Halfa and Reda, 2015). Non-destructive test shows that produced steel rod after metal forming and full heat treatment were free from porosity, holes, pipes and other surface defects. Table 1 shows the designed chemical composition of testing steel.
Microstructure
The microstructure of the investigated steels can be discussed from the micrograph photos shown in Figure 1. Based on Figure 1, the microstructure of the investigated steels in the optimum condition of heat treatment essentially consisted of packets of martensite, within prior-austenite grains. The austenite grains, which had transformed into packets of martensite, could still be recognized due to the preferential etching along their boundaries and also due to the fact that the martensite packets within an austenite grain did not extend beyond the respective prior-austenite grain boundary. The martensite substructure could not be observed because of the narrowness of the martensite laths. The substructure of lathe martensite consists predominantly of a high density of tangles dislocations within laths (Schmidt, 1988).
Mechanical properties
The tension ductility properties of testing steels were illustrated in Table 2. The tabulated data represent the effect of molybdenum (Mo), chromium (Cr) and titanium (Ti) on the mechanical properties of investigating steels. The contribution of different alloying elements in ultimate tensile strength indicates that the positive effect of Cr, Mo and Ti may be attributed to inter-metallic precipitation and solid solution strengthening mechanisms of each element as reported elsewhere (Halfa, 2007).
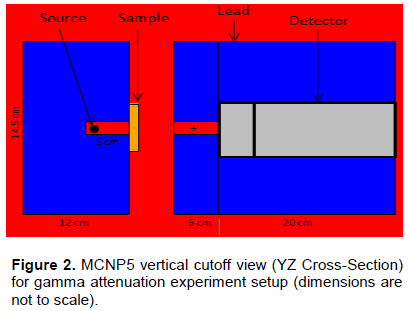
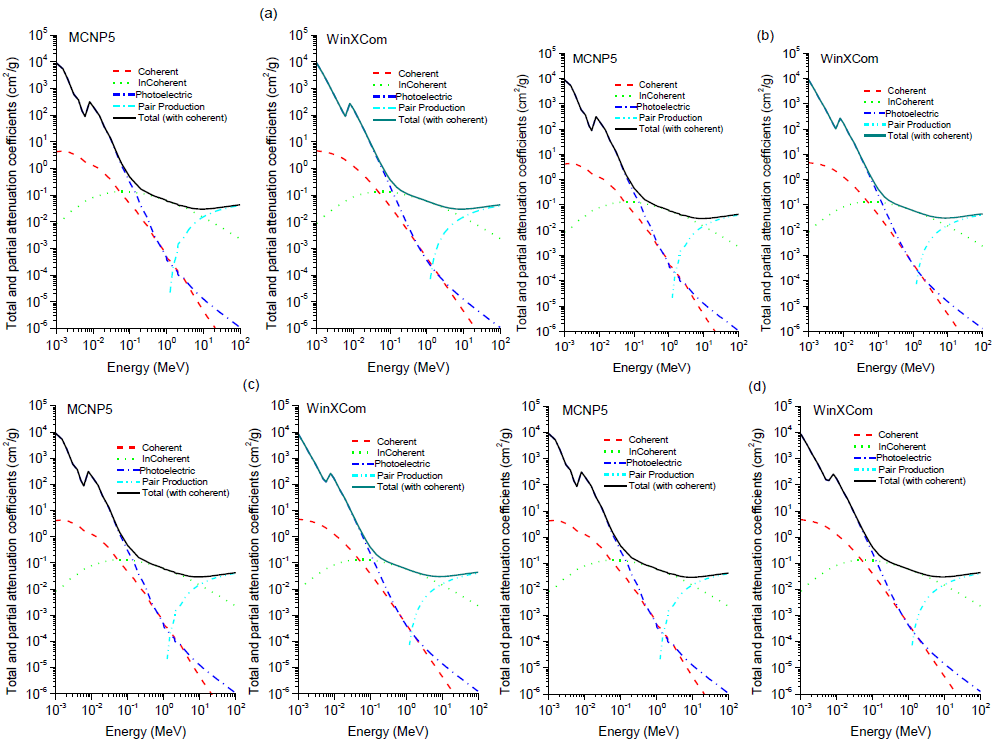
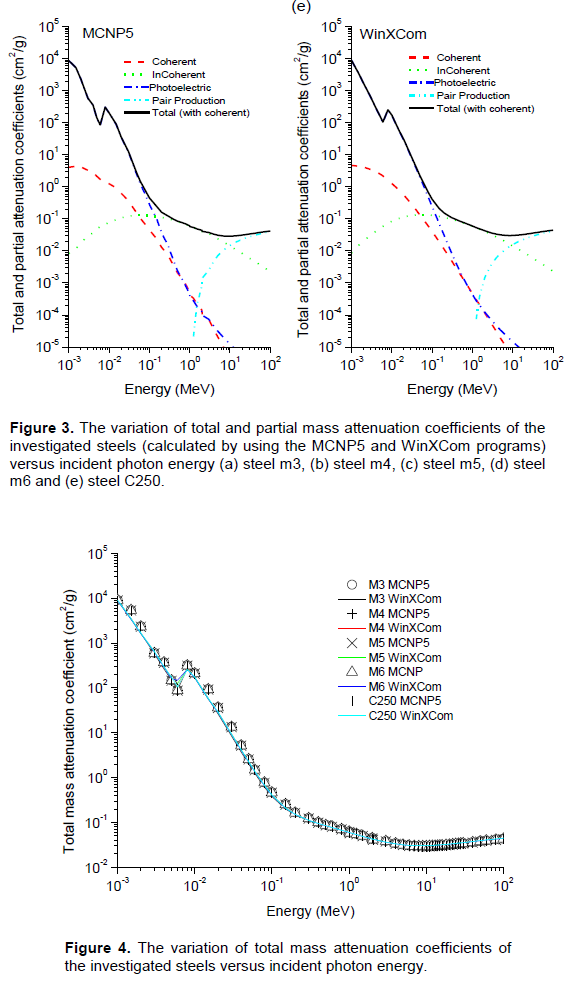
Based on the chemical composition presented in Table 1, MCNP5 and WinXCom programs were used to calculate the total and partial mass attenuation coefficients μ/ρ for the Maraging steels, at the photon energy range of 1 keV–100 MeV. In this study, calculations of MCNP5 (MCNP5, 2003) were performed using the gamma source as a fixed point isotropic source with continuous nuclear cross-section data based on the ENDF/B-VI. The simulation runs with 4 x 107 particle histories, resulting in a total computational time of about 2.14 h. Tally type 4 was used in our calculations to estimate gamma registered in the detector per MeV. cm2. s-1. The statistical uncertainty of the calculated data did not exceed 10% in all energy bins. A schematic diagram of geometry simulated by MCNP5 is shown in Figure 2, with source and detector opening 0.5 cm in radius. Figure 3(a) to (e) shows the variation of total and partial mass attenuation coefficients with the incident photon energy of gamma rays for the steels under investigation. It can be seen from this figure that the total mass attenuation coefficients for the investigated steels decrease with the increase in the incident photon energy. We can notice from Figure 3 that the values of total and partial mass attenuation coefficients calculated by MCNP5 program for all steels under investigation are in good agreement with their theoretical values calculated using WinXCom program. This good agreement can be also seen from the variation of the total mass attenuation coefficient via the incident photon energy presented in Figure 4 for the sake of comparison. It is observed from Figure 4 that the values of μ/ρ decrease very rapidly with an increase in the incident photon energy up to 6 keV for all investigated steels. With the further increase in the incident photon energy up to 8 keV, the values of μ/ρ increase rapidly and are almost the same for all investigated steels. Beyond 8 keV, the μ/ρ values start decrease very rapidly up to 9 MeV. Beyond 9 MeV, the values of μ/ρ start increase slowly as the incident photon energy approaches 100 MeV. The dependence of μ/ρ on incident photon energy can be explained by the dominance of partial processes of interaction of photons with materials (coherent scattering, incoherent scattering, photoelectric absorption and pair production). In the low energy region, as shown in Figure 3, the rapid decrease in the μ/ρ values may be due to the photoelectric absorption, which is the dominant process in the low energy region, where the cross section is inversely proportional to the incident photon energy as E3 and it is also proportional to the atomic number as Z4-5.The decrease in the μ/ρ values in the intermediate energy region (the incident photon energy beyond 8 keV up to 9 MeV) can be explained due to the Compton scattering process (incoherent), whose cross section is inversely proportional to the incident photon energy as E-1 and depends linearly on the atomic number Z. The values of μ/ρ increase slowly beyond 9 MeV due to the pair production process, whose cross section varies approximately as the square of the atomic number Z and is proportional to the incident photon energy as . The values of total mass attenuation coefficients μ/ρ have no obvious difference among all the investigated steels which can be attribute to the Z numbers of the major components in the steel alloys, they are all close to each other (Ni:28, Co:27, Cr:24, Fe:26, Ti:22). The exception is Mo:42, but it only makes up to 4% of the steel. On the other hand, the values of μ/ρ were calculated by using MCNP and WinXCom based on the mixture role which makes the effects of molecular binding and the chemical and crystalline environment are negligible (Sögüt et al., 2001, 2002;). It is worth mentioning that the behaviors of μ/ρ for our investigated steels with the incident photon energy are to some extent comparable with that of shielding materials introduced by (Medhat and Wang, 2015). Also, the values of μ/ρ for the steel under investigation in the present work can be compared with the values measured experimentally, calculated theoretically and simulated for some kinds of alloys (Akkurt, 2009; El-kameesy et al., 2011; Singh et al., 2015). The effective atomic number Zeff values were determined for the steels under investigation by using the MCNP5 and WinXCom values of μ/ρ. The variation of Zeff values versus the incident photon energy was shown graphically in Figure 5, for MCNP5 and WinXCom programs. It is seen from Figure 5 that Zeff values for the investigated steels vary in the low incident photon energy due to the dominance of the photoelectric absorption process in this energy region. It is also seen from Figure 5 that the Zeff values approximately constant in the intermediate and high energy regions. It should be noted that in the low energy region, there is a discrepancy in Zeff values of MCNP5 program. This discrepancy may be due to the sensitivity of MCNP5 experiment setup for low incident photon energy and its value does not exceed 16%. The variation of the effective electron number Neff values against the incident photon energy for steels under study is shown graphically in Figure 6. It is clearly shown by Figure 6 that the energy dependence of Neff is similar to the effective atomic number Zeff, because of the linear relation between them as given by Equation 7.
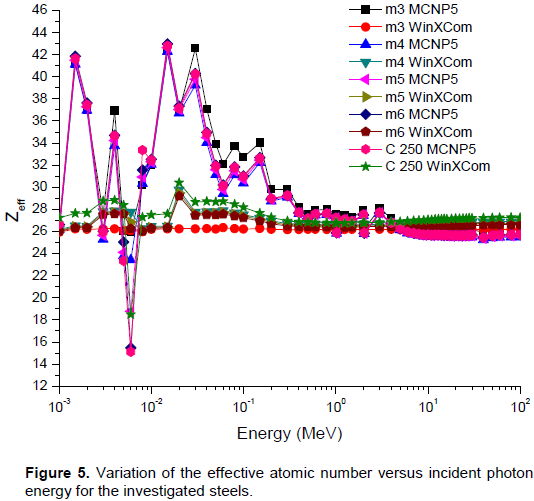
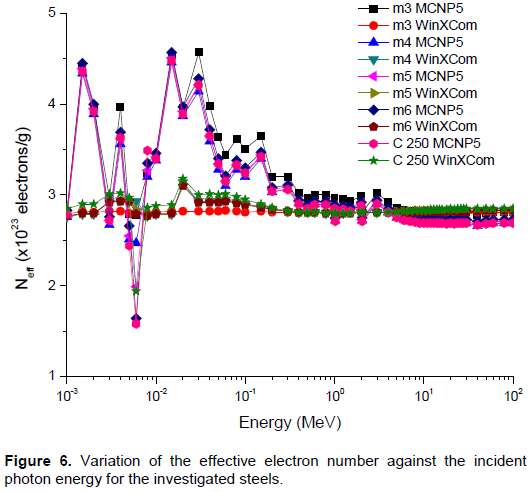
In the present study the partial and total mass attenuation coefficients, effective atomic number and effective electron number have been calculated for different Maraging steel compositions by using the two programs (MCNP5 and WinXCom) over a wide range of incident photon energies from 1 keV to 100 MeV. It was found that the results of μ/ρ, Zeff and Neff are dependent on the incident photon energy, affected by the different photon interaction processes (coherent scattering, incoherent scattering, photoelectric absorption and pair production).The calculated results of μ/ρ, Zeff and Neff by using MCNP5 program were comparable with the theoretical results of WinXCom program. The results also show that there is no difference between the different compositions of the investigated steels as gamma attenuator. The present study also showed that the values of shielding parameters μ/ρ, Zeff and Neff of cobalt free steels (m3-m6) are in agreement with the values of shielding parameters as the standard steel C250. The presented data in this work nominate the investigated steels to be used in nuclear fields as a gamma ray shielding materials especially when moderate to high strength steel was needed.
The authors have not declared any conflict of interests.
REFERENCES
|
Akkurt I, El-Khayatt AM (2013b). Effective atomic number and electron density of marble concrete. J. Radioanal. Nucl. Chem. 295:633-638.
Crossref
|
|
|
|
Akkurt I (2009). Effective atomic and electron numbers of some steels at different energies. Ann. Nucl. Energy 36:1702-1705.
Crossref
|
|
|
|
Baltas H, Celik S, Cevik U, Yanmaz E (2007). Measurement of mass attenuation coefficients and effective atomic numbers for MgB2 superconductor using Xray energies. Radiat. Meas. 42:55-60.
Crossref
|
|
|
|
Baltas H, Cevik U (2008). Determination of the effective atomic numbers and electron densities for YBaCuO superconductor in the range 59.5–136 keV. Nucl. Instrum. Methods Phys. Res. Section B. 266:1127-1131.
Crossref
|
|
|
|
Celik A, Cevik U, Bacaksiz E, Celik N (2008). Effective atomic numbers and electron densities of CuGaSe2 semiconductor in the energy range 6–511 keV. X-Ray Spectrometry. 37:490-494.
Crossref
|
|
|
|
EL-Kameesy SU, Halfa H, EL-Gammam YA (2011). "Maraging steel as a gamma rays shielding material". Isotope Radiat. Res. 43(3):717-725.
|
|
|
|
El-Khayatt AM, Ali AM, Singh Vishwanath P (2014). Photon attenuation coefficients of Heavy-Metal Oxide glasses by MCNP code, XCOM program and experimental data: A comparison study. Nucl. Instrum. Meth. A. 735:207-212.
Crossref
|
|
|
|
Elmahroug Y, Tellili B, Souga C (2015). Determination of total mass attenuation coefficients, effective atomic numbers and electron densities for different shielding materials. Ann. Nucl. Energy 75:268-274.
Crossref
|
|
|
|
Gounhalli SG, Shantappa A, Hanagodimath SM (2012a). Studies on effective atomic numbers and electron densities of some chemical explosives in the energy range 1KeV – 100 GeV. J. Chem. Pharma. Res. 4(5):2545-2563.
|
|
|
|
Gounhalli SG, Shantappa A, Hanagodimath SM (2012b). Studies on Mass Attenuation Coefficient, Effective Atomic Numbers and Electron Densities of Some Narcotic Drugs in the Energy Range 1KeV -100GeV. IOSR J. Appl. Phys. 2 (4):40-48.
Crossref
|
|
|
|
Gowda S, Krishnaveni S, Gowda R (2005). Studies on effective atomic numbers and electron densities in amino acids and sugars in the energy range 30–1333 keV. Nucl. Instrum. Methods B. 239:61–369.
Crossref
|
|
|
|
Gowda S, Krishnaveni S, Yashoda T, Umesh TK, Gowda R (2004). Photon mass attenuation coefficients, effective atomic numbers and electron densities of some thermoluminescent dosimetric compounds. Pramana J. Phys. 63:529-541.
Crossref
|
|
|
|
Halfa H (2007). Improvement of Maraging Steels Using Electro-Slag Remelting Technology. PhD Thesis, Faculty of Engineering, Cairo University, Cairo.
|
|
|
|
Halfa H, Reda AM (2015). Electroslag Remelting of High Technological Steels. J. Min. Mat. Characterization Eng. 3:444-457.
Crossref
|
|
|
|
Han I, Demir L (2009a). Determination of mass attenuation coefficients, effective atomic and electron numbers for Cr, Fe and Ni alloys at different energies. Nucl. Instrum. Methods Phys. Res. Section B. 267:3-8.
Crossref
|
|
|
|
Han I, Demir L (2009b). Mass attenuation coefficients, effective atomic and electron numbers of Ti and Ni alloys. Radiat. Measure. 44:289–294.
Crossref
|
|
|
|
Han I, Demir L (2009c). Studies on effective atomic numbers, electron densities from mass attenuation coefficients in TixCo1_x and CoxCu1_x alloys. Nuclear Instruments and Methods in Physics Research Section B. 267:3505–3510.
Crossref
|
|
|
|
Hine GJ (1952). The "effective" atomic numbers of materials for various gamma-ray interactions. Phys. Rev. 85:725.
|
|
|
|
Hossam H, Ayman F, Mohamed K, Mamdouh E, Kamal El-F (2010). Enhancement of mechanical properties of developed Ti-containing Co-free low Ni maraging steel by ESR. STEEL GRIPS. No. Product & Quality, 8:278-284.
|
|
|
|
Hubbell JH (1982). Photon mass attenuation and energy-absorption coefficients. Int. J. Appl. Radiat. Isot. 33:1269-1290.
Crossref
|
|
|
|
Hubbell JH (1999). Review of photon interaction cross section data in the medical and biological context. Phys. Med. Biol. 44 R1.
Crossref
|
|
|
|
Hubbell JH, Seltzer SM (1995). Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients from 1 keV 20 MeV for elements Z = 1 to 92 and 48 additional substances of dosimetric interest. NISTIR, 5632.
|
|
|
|
Içelli O, Yalçina Z, Okutana M, lub R, Boncukçuog S, en A (2011). The determination of the total mass attenuation coefficients and the effective atomic numbers for concentrated colemanite and Emet colemanite clay. Ann. Nucl. Energy 38:2079-2085.
Crossref
|
|
|
|
Kaur G, Singh K, Lark BS, Sahota HS (2000). Photon interaction studies in solutions of some alkali metal chlorides-I. Radiat. Phys. Chem. 58:315-323.
Crossref
|
|
|
|
Kurudirek M (2014). Effective atomic numbers and electron densities of some human tissues and dosimetric materials for mean energies of various radiation sources relevant to radiotherapy and medical applications. Radiat. Phys. Chem.102:139-146.
Crossref
|
|
|
|
Limkitjaroenporn P, Kaewkhao J, Asavavisithchai S (2013). Determination of mass attenuation coefficients and effective atomic numbers for Inconel 738 alloy for different energies obtained from Compton scattering. Ann. Nucl. Energy 53:64-68.
Crossref
|
|
|
|
Manjunathaguru V, Umesh TK (2007). Total interaction cross sections and effective atomic numbers of some biologically important compounds containing H, C, N and O in the energy range 6.4–136 keV. J. Phys. B: Atomic Mol. Opt. Phys. 40:3707-3718.
Crossref
|
|
|
|
Manohara SR, Hanagodimath SM (2007a). Effective atomic numbers for photon energy absorption of essential amino acids in the energy range 1 keV to 20 MeV. Nucl. Instrum. Methods Phys. Res. Section B. 264:9-14.
Crossref
|
|
|
|
Manohara SR, Hanagodimath SM (2007b). Studies on effective atomic numbers and electron densities of essential amino acids in the energy range 1 keV–100 GeV. Nucl. Instrum. Methods Phys. Res. Section B. 258:321-328.
Crossref
|
|
|
|
Manohara SR, Hanagodimath SM, Gerward L (2008a). Energy dependence of effective atomic numbers for photon energy absorption and photon interaction: studies of some biological molecules in the energy range 1 keV– 20 MeV. Med. Phys. 35:388-402.
Crossref
|
|
|
|
Manohara SR, Hanagodimath SM, Gerward L (2008b). Studies on effective atomic number, electron density and kerma for some fatty acids and carbohydrates. Phys. Med. Biol. 53:N377–N386.
Crossref
|
|
|
|
Manohara SR, Hanagodimath SM, Gerward L (2009a). The effective atomic numbers of some biomolecules calculated by two methods: a comparative study. Med. Phys. 36:137-141.
Crossref
|
|
|
|
Manohara SR, Hanagodimath SM, Thind KS, Gerward L (2010). The effective atomic number revisited in the light of modern photon-interaction cross-section databases. Applied Radiation and Isotopes. 68:784-787.
Crossref
|
|
|
|
Manoharaa SR, Hanagodimath SM, Gerward L (2009b). Photon interaction and energy absorption in glass: A transparent gamma ray shield. J. Nucl. Mater. 393:465-472.
Crossref
|
|
|
|
MCNP5 (2003). MCNP - A General Monte Carlo N-Particle Transport Code: V. 5, vol. I (LA-UR-03e1987) and vol. II (LA-CP-0245), Los Alamos National Laboratory.
|
|
|
|
Medhat ME, Wang YF (2015). Investigation on radiation shielding parameters of oxide dispersion strengthened steels used in high temperature nuclear reactor applications. Ann. Nucl. Energy 80:365-370.
Crossref
|
|
|
|
Prasad SG, Parthasaradhi K, Bloomer WD (1998). Effective atomic numbers for photoabsorption in alloys in the energy region of absorption edges. Radiat. Phys. Chem. 53:449-453.
Crossref
|
|
|
|
Schmidt ML (1988). In Maraging Steels: Recent Developments and Applications, the Materials, Metals & Materials Society, Edited by Richerd K. Wilson.
|
|
|
|
Sha W, Cerezo A, Smith GDW (1993). Phase chemistry and precipitation reactions in Maragingsteels: Part IV. Discussion and conclusions. Metallurgical Trans. A. 24:1251-1256.
Crossref
|
|
|
|
Sidhu BS, Dhaliwal AS, Mann KS, Kahlon KS (2012). Study of mass attenuation coefficients, effective atomic numbers and electron densities for some low Z compounds of dosimetry interest at 59.54 keV incident photon energy. Ann. Nucl. Energy 42:153-157.
Crossref
|
|
|
|
Singh S, Kumar A, Singh D, Singh KT, Mudahar GS (2008). Barium–borate–flyash glasses: as radiation shielding materials. Nucl. Instrum. Methods Phys. Res. Section B. 266:140-146.
Crossref
|
|
|
|
Singh VP, Medhat ME, Shirmardi SP (2015). Comparative studies on shielding properties of some steel alloys using Geant4, MCNP, WinXCOM and experimental results. Radiat. Phys. Chem. 106:255-260.
Crossref
|
|
|
|
Sögüt Ö, Çolak S, Büyükkasap E, Küçükönder A (2002). Chemical effect on total mass attenuation coefficients of V, Cr, Mn, Co and Ni. J. Radioanal. Nucl. Chem. 251:135-138.
Crossref
|
|
|
|
Sögüt Ö, Sevena S, Baydas E, Büyükkasap E, Küçükönder A (2001). Chemical effects on Kβ/Kα X-ray intensity ratios of Mo, Ag, Cd, Ba, La, Ce compounds and total mass attenuation coefficients of Fe and Cu. Spectrochimica Acta Part B 56:1367-1374.
Crossref
|
|
|
|
Taylor ML, Franich RD, Trapp JV, Johnston PN (2008). The effective atomic number of dosimetric gels. Australasian Phys. Eng. Sci. Med. 31:131-138.
Crossref
|
|
|
|
Un A, Sahin Y (2011). Determination of mass attenuation coefficients, effective atomic and electron numbers, mean free paths and kermas for PbO, barite and some boron ores. Nucl. Instrum. Methods Phys. Res. B. 269:1506-1511.
Crossref
|
|
|
|
Un A, Sahin Y (2012). Determination of mass attenuation coefficients, effective atomic numbers, effective electron numbers and kermas for Earth and Martian soils. Nucl. Instrum. Methods Phys. Res. B. 288:42-47.
Crossref
|
|
|
|
Un A, Caner T (2014). The Direct-Zeff software for direct calculation of mass attenuation coefficient, effective atomic number and effective electron number. Ann. Nucl. Energy 65:158-165.
Crossref
|
|
|
|
Vasudevan VK, Kim SJ, Wayman CM (1990). Precipitation reactions and strengthening behavior in 18 Wt Pct nickel Maraging steels. Metallurgical Transactions A. 21:2655-2668.
Crossref
|
|
|
|
Vaz P (2009). Neutron transport simulation (selected topics). Radiat. Phys. Chem. 78:829.
Crossref
|