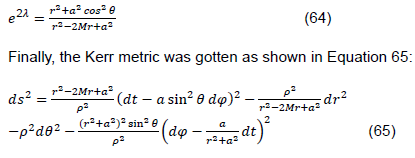ABSTRACT
Einstein's general relativistic field equation is a nonlinear partial differential equation that lacks an easy way to obtain exact solutions. The most famous of which are Schwarzschild and Kerr's black hole solutions. Kerr metric has astrophysical meaning because most cosmic celestial bodies rotate. Kerr metric is even harder than Schwarzschild metric to be derived directly due to off-diagonal term of metric tensor. In this paper, a derivation of Kerr metric was obtained by ellipsoid coordinate transformation which causes elimination of large amount of tedious derivation. This derivation is not only physically enlightening, but also further deducing some characteristics of the rotating black hole.
Key words: General relativity, Schwarzschild metric, Kerr metric, ellipsoid coordinate transformation, exact solutions.
The theory of general relativity proposed by Albert Einstein in 1915 was one of the greatest advances in modern physics. It describes the distribution of matter to determine the space-time curvature, and the curvature determines how the matter moves. Einstein's field equation is very simple and elegant, but based on the fact that the Einstein' field equation is a set of nonlinear differential equations, it has proved difficult to find the exact analytic solution. The exact solution has physical meanings only in some simplified assumptions, the most famous of which is Schwarzschild and Kerr's black hole solution, and Friedman's solution to cosmology. One year after Einstein published his equation, the spherical symmetry, static vacuum solution with center singularity was found by Schwarzschild (Schwarzschild, 1916). Nearly 50 years later, the fixed axis symmetric rotating black hole was solved in 1963 by Kerr (Kerr, 1963). Some of these exact solutions have been used to explain topics related to the gravity in cosmology, such as Mercury's precession of the perihelion, gravitational lens, black hole, expansion of the universe and gravitational waves.
Today, many solving methods of Einstein field equations are proposed. For example: Pensose-Newman's method (Penrose and Rindler, 1984) or Bäcklund transformations (Kramer et al., 1981). Despite their great success in dealing with the Einstein equation, these methods are technically complex and expert-oriented.
The Kerr solution is important in astrophysics because most cosmic celestial bodies are rotating and are rarely completely at rest. Traditionally, the general method of the Kerr solution can be found here, The Mathematical Theory of Black Holes, by the classical works of Chandrasekhar (1983). However, the calculation is so lengthy and complicated that the College or Institute students also find it difficult to understand. Recent literature review showed that it is possible to obtain Kerr metric through the oblate spheroidal coordinate’s transformation (Enderlein, 1997). This encourages me to look for a more concise way to solve the vacuum solution of Einstein's field equation.
The motivation of this derivation simply came from the use of relatively simple way of solving Schwarzschild metric to derive the Kerr metric, which can make more students to be interested in physics for the general relativity of the exact solution to self-deduction.
In this paper, a more enlightening way to find this solution was introduced, not only simple and elegant, but also further deriving some of the physical characteristics of the rotating black hole.
SCHWARZSCHILD AND KERR SOLUTIONS
The exact solution of Einstein field equation is usually expressed in metric. For example, Minkowski space-time is a four-dimension coordinates combining three-dimensional Euclidean space and one-dimension time can be expressed in Cartesian form as shown in Equation 1. In all physical quality, we adopt c = G = 1.
However, Schwarzschild metric cannot be used to describe rotation, axial-symmetry and charged heavenly bodies. From the examination of the metric tensor

in Schwarzschild metric, one can obtain the components:
Where a is the coordinate transformation parameter. The metric under the new coordinate system becomes Equation 9:
Equation 20 can be found in the literature and also textbook by O’Neil. It is also called Kerr metric with Boyer-Lindquist in orthonormal frame (O'Neil, 1995). There is no off-diagonal terms, and after the coordinate transformation.
CALCULATING THE RICCI TENSOR
From pervious discussion, Equation 9 can be recognized as the coordinate under the ellipsoid symmetry in vacuum. Therefore, when the mass M approached 0, Kerr metric Equation 20 will also be transformed into Equation 21, which equals Equation 9. The differences of metric tensor components are in time-time and radial-radial terms, just the same as between Schwarzschild metric (Equation 4) and Minkowski space-time (Equation 2). and defined in Equation 22 are ellipsoid coordinate transformation functions.
FINDING A SOLUTION OF THE VACCUM EINSTEIN FIELD EQUATIONS
To solve vacuum Einstein's field equations, first, the Ricci tensor was set to zero, which means: ,in the empty space, θ is approximately constant. Then combine with R00 and R11 to get Equation 55, and solve the equation, Equations 56 to 58 were obtained:
It is proved that Kerr metric equation (Equation 65) can be obtained by combining the ellipsoid coordinate transformation and the assumptions listed in Equations 21 to 23 following these steps: transforming the Euclidian four-dimension space-time in Equation 1 to vacuum Minkowski space-time with ellipsoid symmetry in Equation 9; transforming from to under the new coordinate system to eliminate the major difference in metric tensor components between Kerr metric and Schwarzschild metric, and the product of and becomes -1; solving vacuum Einstein’s equation by using Schwarzschild method from Equation 23; applying limit method to calculate Ricci curvature tensor; and finally deducting Kerr metric.
Table 1 shows the list of the metric tensor components discussed in previous sections, including the Minkowski space-time, the Schwarzschild solution, empty ellipsoid, a Schwarzschild-like ellipsoid solution and the Kerr solution. The Minkowski space-time and the Schwarzschild solution have spherical symmetry, and the others have ellipsoid symmetry.
Further, some of characteristics with deeper physics meaning of ellipsoid symmetry, Kerr metric and rotating black hole can be obtained from this new coordinate function . Remember when a approaches to zero , degenerate to .
Ellipsoid symmetry and Kerr metric
While metric with spherical symmetry in vacuum has the following expression:
In this paper, the Kerr metric was derived from the coordinate transformation method. Firstly, the Kerr Metric was obtained with Boyer-Lindquist in orthonormal frame, and then it was proven that it is possible to derive the Kerr metric from the vacuum ellipsoid symmetry, and this derivation allows us to better understand the physical properties of the rotating black hole, such as the frame-dragging effect, the angular velocity. This deduction method is different from classical papers written by Kerr and Chandrasekhar, and is expected to encourage future study in this subject.
The authors have not declared any conflict of interests.
REFERENCES
|
Bijan N (2011). Schwarzschild-Like Solution for Ellipsoidal Celestial Objects. Int. J. Phys. Sci. 6(6):1426-1430.
|
|
|
|
Chandrasekhar S (1983). The Mathematical Theory of Black Holes. Oxford U.P., New York pp. 273-318.
|
|
|
|
|
Enderlein J (1997). A heuristic way of obtaining the Kerr metric. Am. J. Phys. 65(9):897-902
Crossref
|
|
|
|
|
Everitt CWF, DeBra DB, Parkinson BW, Turneaure JP, Conklin JW, Heifetz MI, Keiser GM, Silbergleit AS, Holmes T, Kolodziejczak J, Al-Meshari M (2011). Gravity Probe B: Final results of a space experiment to test general relativity. Phys. Rev. Lett. 106:221101.
Crossref
|
|
|
|
|
Kerr RP (1963). Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 11:237-238.
Crossref
|
|
|
|
|
Kramer D, Stephani H, MacCallum M, Herlt E (1981). Exact Solutions of Einstein's Equations. Cambridge U.P., Cambridge.
|
|
|
|
|
Landau L, Lifshitz E (1987). The Classical Theory of Relativity. Vol. 2, Pergamon Press.
|
|
|
|
|
O'Neil B (1995). The Geometry of Kerr Black Holes. Peters AK, Wellesley, Mas- sachusetts. P 69.
|
|
|
|
|
Penrose R, Rindler W (1984). Spinors and Space-Time. Cambridge U.P., Cambridge.
Crossref
|
|
|
|
|
Schwarzschild K (1916). On the Gravitational Field of a Point-Mass, According to Einstein's Theory," (English translation). Abraham Zelmanov J. 1:10-19.
|
|