The limitations of PMF 56 method have led researchers to develop other alternatives, for example: empirical methods. These methods are very simple to use and require few variables in relation to the PMF 56 method. According to Valipour (2015), empirical methods include mass transfer methods, tank evaporation methods, methods based on solar radiation and air temperature (method most used). Some methods based on temperature are: Hargreaves and Samani-HS, Hamon-Ham, Mc Cloud-McC, Blaney and Criddle-BC and on solar radiation are: Makkink-Mak, Turc, Priestley and Taylor-PT and Ravazzani-Rav. Shiri et al. (2014), using meteorological data of nine years verified that the HS method exceeded the efficiency of Mak, Turc and PT methods. On other hand, Sabziparvar and Tabari (2010) observed that HS method overcame the efficiency of Mak and PT methods in arid and semi-arid conditions of Iran. Many other authors reported better efficiency of temperature methods than solar radiation methods (Djaman et al., 2015; Ahooghalandari et al., 2016). However, opposite result reported by Liu et al. (2017) in their study, revealed that Mak method was better in estimation ETo than temperature-based methods of Ham, BC and McC. In addition, Mak method was found better than HS method in arid, semi-arid and Mediterranean conditions of Iran by Valipour at al. (2017).

The results presented show that there is a variability of the efficiency of empirical methods. Thus, it is essential to evaluate their efficiency for each site, under the risk of select methods that underestimate or overestimate the real ETo value, consequently, reducing agricultural productivity and product quality.

The main goal of the present research was to evaluate the efficiency of eight empirical methods based on temperature and six on solar radiation against PMF 56 method in Vilankulo district.

 

Study area and data collection

Vilankulo district was located in Inhambane province of Mozambique (LAT 22°36'S; LONG 35°19'E; and 20 m OSL). Based on Köppen climatic classification, Vilankulo district shows an Aw climate (humid tropical climate with dry  winter  and  summer  rains) with a monthly average temperature of 24.4°C, annual total precipitation of 761.5 mm and an annual total ETo of 1804.9 mm. The data used correspond to 1980 to 2009 (30 years) period.

Then, data of maximum temperature (Tx), minimum temperature (Tn) and average temperature (T), relative humidity (RH), wind speed (U₂) and sunshine hours (n) were collected in the National Institute of Meteorology of Mozambique (period from 1979 to 2006). The data of the other years were discarded since they presented numerous failures. In case study period, some failures were observed and filled using mathematical methods. For Tx, Tn, T and RH data, missing values were considered equal to the average of the existing values​​ in a given period. For U₂, the missing data was considered equal to 2 m s^-1 based on the recommendation by Allen et al. (1998). In Table 1, are presented the collected monthly average meteorological data from 1979 to 2006.

 

 

After the described procedure, the ETo was estimated using eight empirical methods based on air temperature and six based on solar radiation. All empirical methods were evaluated in relation to PMF 56 method. Based on the fact that it is necessary to use global solar radiation (Rs) in PMF 56 method, it was estimated from Equation 1 and the results were put in Table 1. According to Allen et al. (1998), in Rs data absence and local calibration of parameters a and b of Equation 1, the following values ​​are adopted: a = 0.25 and b = 0.50. The equations used in the PMF 56 method and in empirical methods are presented in Table 2.

 

 

Where: Rs- global solar radiation (MJ m^-2 day^-1); Ra- extraterrestrial radiation (MJ m^-2 day^-1); n- sunshine hours (n); N- photoperiod; a & b- constant of the Angstrom equation.

Evaluation of empirical methods

The efficiency of empirical methods was evaluated in relation to PMF 56 method based on statistical parameters like: Mean Bias Error (MBE), Root Mean Square Error (RMSE), "d" (Willmott coefficient) and based on R² (coefficient of determination). The significance of each method in relation to PMF 56 method was analyzed based on t-test at significance level of 5%. MBE > 0 indicates overestimate and the opposite underestimate. RMSE indicates method accuracy and "d" indicates the agreement. The best methods should present the following results: MBE ≅ 0; RMSE ≅ 0; “d “≅ 1 and R² ≅ 1. Equations 2; 3; 4 and 5 were used to calculate the MBE, RMSE, "d" and R² parameters, respectively.

Where: ETo_Est- values estimated by the methods (mm day^-1); ETo_PMF56 -values estimated by the standard method (mm day^-1); N- number of estimates per period and 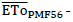 mean ETo estimated by the standard method (mm day^-1);  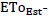mean ETo estimated by the appraised methods (mm day^-1).

 

 

 

 

Estimation of ETo from temperature-based methods

Table 3 shows the statistical efficiency of empirical methods based on temperature in Vilankulo district from 1979 to 2006. All methods correlated significantly (p < 0.05) with PMF 56 method, R² values ranging from 0.55 (Rom method) to 0.94 (HSm method). The R² values of each method are shown in Figure 1(a-h).

Observing Table 3, all methods underestimated ETo estimated by the PMF 56 method (MBE < 0), with the exception of the McC, McG and Kha methods which overestimated. In terms of absolute value of MBE, the Sch method presented the closest value of zero (MBE = -0.09 mm day ^-1 = 1.8%), showing the tendency to be the best method for estimating ETo in the district of Vilankulo. The worst MBE result was observed in the McC method (MBE = 1.97 mm day^-1 = 39.4%). Jakimavičius et al. (2013) found that the Sch method underestimated ETo by 0.6%, but overestimate results were reported in Namanye (MBE = 39%) and Fanaye (MBE = 10%) by Djaman et al. (2015).

 

 

 

In relation to the RMSE values, the best accuracy was observed in Sch method (RMSE = 0.81 mm day^-1) and the worst in McC method (RMSE = 2.11 mm day^-1), reinforcing the observed results from MBE parameter. The result observed in Sch method was already predictable since it presented the mean value of ETo (ETo = 4.92 ± 0.74 mm day^-1) closest to mean value obtained by PMF 56 method (ETo = 5.01 ± 1.34 mm day^-1), Table 3. In addition, this method presented the parameter "d" = 0.84 which can be considered close to 1, indicating a good agreement with the PMF 56 method. In Ndiaye and Fanaye, the Sch method presented an accuracy of 2.65 and 4.33 mm day^-1, respectively, according to Djaman et  al.  (2015).  Tabari  et  al.  (2013) observed the following efficiency: MBE = -0.86 mm day^-1; RMSE = 1.03 mm day^-1 and R² = 0.87. In 31 provinces of Iran, Valipour (2015) reported that Sch method presented values ​​of R² ranging from 0.85 to 0.96. Some of these results are inferior to those presented in the present research, evidencing that efficiency of the empirical methods can vary from place to place.

Similarly, in line with this study, Liu et al. (2017) evaluated different ETo estimation methods and did not recommend the use of McC method. However, in Chapadão do Sul, Brazil, McC method was recommended to estimate ETo at different time scales by Cunha et al. (2012), showing the need to choose methods carefully.

From Table 3, it was also observed that the t-test results showed that only Sch method is not statistically different with PMF 56 method in ETo estimation at 5%. Thus, Sch method can be safely used instead of PMF 56 method. The use of Sch method instead of PMF 56 method is extremely advantageous as this method requires the use of meteorological data (T and RH) which are available at several meteorological stations than those required in PMF 56.

Estimation of ETo from methods based on solar radiation

Table 4 shows the efficiency of empirical methods based on solar radiation, from 1979 to 2006, similarly to temperature-based methods, a significant correlation was observed with PMF 56 method (p < 0.05), with R² = 0.98 in all methods, as indicated in Figure 1(i-n).

With the exception of JHa and Mam methods, all methods underestimated PMF 56 method. The best result is observed in Mak method (MBE = 0.03 mm day^-1) and worse  in  JHa method (MBE = 0.88  mm day^-1).  The best result of Mak method is confirmed by RMSE parameter which presented a value closer to zero (RMSE = 0.28 mm day^-1), meaning high precision. The worst result observed through MBE parameter is also confirmed by RMSE parameter (0.94 mm day^-1) which was the highest, indicating lower precision (Table 4). In relation to the mean ETo values, is also observed that JHa method (ETo = 5.90 ± 1.59 mm day^-1) was worse than Mak method (ETo = 4.98 ± 0.97 mm day^-1), since the last method estimated a closer value to the method of PMF 56 (ETo = 5.01 ± 1.34 mm day^-1).

 

 

Mohawesh (2011), when evaluating eight methods of ETo estimation in the arid and semi-arid conditions of Jordan obtained the following performance with Mak method: MBE = 2.63 mm day^-1; RMSE = 3.72 mm day^-1 and R² = 0.45; MBE = 1.82 mm day^-1; RMSE = 2.52 mm day^-1 and R² = 0.57, respectively. The efficiency obtained by this author is lower than that reported in this research. Other lower results were reported by Liu et al. (2017). These researches were carried out under dry climate conditions and Mak method is indicated as the proper for these conditions. However, in the current paper research (humid tropical climate), Mak method presented better efficiency. With this, the climate of Vilankulo district probably has a tendency to be dry, being necessary to use other climatic classifications (out of our scope) to better understand Vilankulo's climate. According to Vianello and Alves (2012), Köppen climatic classification has  the  limitation  of   not   having   a  rational   basis   in temperature and rainfall selection values.

Also in Table 4, it was observed that Mak method, similar to some methods, showed high agreement rate with the PMF 56 method ("d" = 0.97). On the other hand, unlike the other methods evaluated, Mak method did not show statistically significant differences in ETo estimation in relation to PMF 56 method by the t-test, reinforcing that this method is the best for estimation of ETo among evaluated methods.

Comparison of all empirical methods

Methods were analyzed and judged based on RMSE parameter (Table 5) such as criterion used by Liu et al. (2017). To facilitate understanding of Table 5, the asterisked methods are based on solar radiation and those without asterisks are based on temperature.

 

 

In comparison of all methods, it was verified that Mak radiation method occupied the first position (RMSE = 0.28 mm day^-1) and McC  temperature  method  occupied the last position (RMSE = 2.11 mm day^-1) (Table 5). All temperature-based methods presented a lower accuracy than those based on solar radiation, although the Sch method occupied the 4^th position (RMSE = 0.81 mm day^-1). The tendency of the solar radiation methods to produce better results in relation to temperature methods was reported in several studies (Tabari et al., 2013; Valipour et al., 2017), corroborating to present research.

If it is impossible to measure Rs or to be estimated (which is one of parameter necessary for Mak method use), Sch method can be used as an alternative, which requires less parameter such as T and RH. In addition, T and RH are measured in almost all meteorological gauges in worldwide. Although, Mak method presented the best result of present research, Sabziparvar and Tabari (2010) and Liu et al. (2017) found that efficiency of this method was less to some methods evaluated in this study case. Therefore, if it requires the use of Mak method in different conditions detailed in this research, its efficiency should be assessed first in order to check the risk on application of improper irrigation. Figure 1(i-n) confirms the tendency of solar radiation methods to estimate ETo better; hence, presenting high mathematical adjustments (R² ≅ 1), they presented regression lines closer to the line y = x.

 

 

 

 

Among temperature-based methods, Schendel (Sch) method showed better efficiency (MBE = -0.09 mm day^-1; RMSE = 0.81 mm day^-1; “d” = 0.84 and R² = 0.74), whereas among solar radiation-based methods, the original Makkink (Mak) method presented the best efficiency (MBE = -0.03 mm day^-1; RMSE = 0.28 mm day^-1, "d" = 0.97 and R² = 0.98). Both methods were not statistically different with Penman Monteith FAO 56 standard method by t-test.

Comparing all methods through RMSE parameter, it was concluded that Mak method occupied the 1^st position. If it is not possible to measure or to estimate global solar radiation (Rs), instead of Mak method, the Sch method can be used as an alternative. This method requires only data of air temperature and relative humidity, which are usually measured in several stations.

 

The authors have not declared any conflict of interests.