ABSTRACT
Nowadays, modeling is increasingly used as a method for determination of the mechanical and hydraulic behavior of the rock mass. In this paper, with regard to the high importance of joint persistence characteristic on the mechanical and hydraulic behavior of the rock mass, geometric-stochastic joint network model has been developed by considering the statistical characteristics of joint size based on Veneziano model. With the use of surveyed data in the right bank of Rudbar Lorestan dam plant and estimation of the best probability distribution function on geometric characteristics of existing joint sets in this region, the three-dimensional geometric model of joint network has been developed. In order to model implementation, a computer code written in C++, called FRAC3D, has been developed that is able to represent the joint network in different directions and to generate text outputs. The results of this model can be a useful input for numerical stability analysis and hydraulic behavior studies of rock mass.
Key words: Geometrical-Stochastic modeling, joint network, joint surveying, statistical studies.
Joints are the most common of rock mass discontinuities including pores, fractures, joints, faults and bedding planes (Sari, 2009). Rock joint networks and its geometrical features are the most effective factors on permeability, deformability, strength and stability of rock masses (Hudson and Harrison, 1997).
Investigation of the fluid current behaviour in rocky environments is of prominent significance in civil, mining and environmental activities, such as burial of dangerous atomic residue, as well as oil and geothermal energy. However, precise estimation of rock mass strength is one of the main requirements for planning and implementing of civil and mining projects in the rock.
Developing a fluid current model or studying the mechanical behaviour of joint rock masses, initially needs designing a geometrical model of joint networks based on geometrical data obtained from the earth. In other words, the main issue in rock mass modelling is to attain
precise three-dimensional description of rock mass structures through the collected data (Flynn and Pine, 2007). The success of discontinuous-numerical analyses is totally due to geometrical model designing.
There will always be some random variation in the geometric properties of joints such as dip, dip direction, spacing and persistence by virtue of rock mass heterogeneous nature. Therefore, it is necessary to describe the ordered properties stochastically and to use it in rock mass modeling (Sari, 2009).
Three-dimensional stochastic joint network modeling technique represents the most optimal choice for simulating the probability nature of joint geometric properties. The purpose of producing stochastic joint networks is to produce many joints with geometrical features identical to specific distribution functions in two or three dimensions which reflect the features of the real joints surveyed in the rock mass (Ford et al., 2007).
Stochastic parameters of discontinuities are obtained from the field measurements and statistical analyses. A prominent progress in data collection and analysis in recent years made it possible to collect a bunch of data with high quality from rock mass exposure. Therefore, it would be possible to estimate the features of the rock mass in a more precise manner based on the collected data.
In this paper, with regard to the high impact of joint persistence characteristic on the rock mass mechanical and hydraulic behavior, stochastic fracture network model has been developed by considering the statistical characteristics of joint size based on Veneziano model. In addition, with the use of surveyed data in the right bank of Rudbar Lorestan dam plant and developed stochastic model, the three-dimensional geometric model of joint network has been prepared.
Data processing including fitting of the different probability distribution function on geometric characteristics of surveyed joint sets in this region has been done. In order to implement the model, a computer code has been developed with the use of C++ language programming that is able to represent the joint network in different directions and to generate digital outputs.
Stochastic models of joint networks show the heterogeneous nature of the jointed rock masses through presenting the joint networks as discrete elements in space with geometrical features that are described stochastically. The stochastic fracture network models developed at MIT can be considered as basic prepared models in this field.
The studies undertaken by Hudson and La pointe (1980) and Robinson (1983) on the issue of fluid seepage and current can be considered the starting point of applying stochastic models. Dershowitz and Einstein (1988) presented a stochastic model that provides more realistic joint networks by considering changes in orientation, spacing and persistence of the discontinuities.
Priest and Samaniego (1988) tried to develop this concept to the field of block stability analysis. The hierarchical geometrical model regarding the elementary processes of joint making presented by Reyes and Einstein (1991) and the geometric-mechanical model presented by Martel et al. (1991) are the two other instances of developed stochastic models. The limitations of these models, especially the possibility of modeling for only two joint sets and the problems with making changes to joints distribution, have resulted in designing an advanced two dimensional hierarchical model by Yu (1992).
Priest presented a three-dimensional stochastic model in 1993 in which the joints were considered as circular discs. In this model, stochastic measures for joint diameters are obtained from appropriate distributions provided in Priest’s algorithms (Priest, 1993). Ivanova et al. (1995) developed the advanced two-dimensional hierarchical model to a three dimensional one. Kulatilake et al. (2004) tried to plan a three dimensional stochastic model of joint networks for a rock mass made up of Diorite; they also presented a new process for estimation of the strength and deformability of rock blocks in three dimensions.
In recent years, based on the previous models, stochastic model has been developed more for the purpose of investigating the effects of the correlation between the length and aperture of the joints on hydro-mechanical and mechanical behavior of the jointed rock mass. The two dimensional model presented by Baghbanan and Jing (2008) and the three dimensional model presented by Xu and Dowd (2010) as well as the model presented by Bang et al. (2012) are some instances that support this claim.
The first stage of the modeling process is to collect discontinuity data for statistical analysis. The most common measurement technique is by scanlines, or window survey, of rock outcrops or excavated rock surfaces (Ferrero and Umili, 2011). If drill cores are available, scanlines and/or window surveys can also be applied to core samples (Zhang and Einstein, 2000). Additional data can be obtained along the borehole using down-the-borehole camera, geophysical logging, and the remote methods for mapping exposures such as photogrammetry and laser scanning (Flynn and Pine, 2007).
Geometrical features of the joint are normally determined by surveying the joints along the rock surface through linear or window survey methods. In linear survey method, less judgement is required during the process of data collection, so there is no need for having too much geological experience. On the contrary, more information can be obtained in the vast areas through window surveying, but in specific spots, linear surveying will uncover more details (Zadhesh et al., 2013).
LOCATION AND GEOLOGY OF LORESTAN ROODBAR DAM
The project was undertaken in Lorestan Roodbar dam and hydropower plant in Lorestan province, 100 km far from the southern boundary of Aligoodarz and in the way of Roodbar River. The area under study is located across northern Zagros or high Zagros, which is limited to Zagros folded belt from the Western South and to Zagros main reverse fault and Sanandaj-Sirjan area from Eastern North. Topographically, the average height of this area is about 1750 m and it has a cold and mountainous weather. Based on the height of this area, raining mostly happens in the form of snow.
In the area under study, the most important exposed units are limestone-dolomite formations of the Dalan and Seruk belonging to the Permian period, Hormoz and Mila formations with shale and marl lithology belonging to Cambrian period, Groo formation with marl-limestone and marl belonging to Cretaceous period and Bakhtiary formation which are made up of Conglomerate belonging to Pliocene period. Reverse or thrust faults, which are the main tectonic factors in the area make the rocks appear folded. The faults have a great variety because of being located along Zagros. The overall trend of the area geological structure is from N130°E to N140°E called Zagros trend.
Rock masses constructing the dam wall are mainly made up of carbonaceous with a specific gravity of 2.7 gr/cm3. They have low porosity and also bedding. The thickness of the layers varies from thin layers to the thick ones. The strike of the layers follows the trend of region structure. Normally, the layers have steep dips that vary from 60 to 90°. From the perspective of rock quality designation (RQD), according to the exploratory drillings, rock mass does not have the desired conditions and the average shows a mid to low quality. Furthermore, based on RMR ranking, the quality of rock mass is measured to be mid (Secondly Engineering Geology Report, 2007).
Joint surveys are an integral component of site characterization studies in rock engineering. Measuring on rock exposure has the advantage of using a vast area for surveying. Geometrical features of the discontinuities such as orientation, persistence and other large-scale geometrical features of the discontinuities can be surveyed. Geological relationship between the groups of the discontinuities is also observable in the rock exposures.
The collecting data reported in this paper were obtained from the scanline mapping technique only. The scanline sampling technique involves measuring all the joints that intersect a scanline along its length. The important point is that there is no universally accepted standard for the linear surveying method. In fact, the details of the method must be modified in a way that makes it possible to collect the required data for the desired purpose and accommodate it to the local conditions of the rock (Priest, 1993).
In the scanline mapping technique, a clean, approximately planar rock face is selected that is large relative to the size and spacing of discontinuities. As a rough guide the sample zone should contain between 150 and 350 joints, which about 50% of them should have at least one end visible. The surveyed line has a tape length of 20 to 30 m and is stabilized by two nails along the exposure with the steepest dip. It is better to start the linear surveying method from a discontinuity although it is not necessary. In this method, local condition and orientation of the rock exposure as well as the trend and plunge of the line are recorded (Priest, 1993).
To have a view of the type of termination of the joint trace length in the exposure, let the numbers belonging to three types of traces be p, m and n, for joints which both of the trace censored, one end of trace censored and both ends of the trace observable respectively. Then, R0, R1 and R2 are defined as follows (Zadhesh et al., 2013):
In this paper, right bank of Lorestan Roodbar dam has been chosen for joint surveying (Figure 1). The right bank is located in a Dalan formation made up of gray Dolomite-limestone layers with medium to high thickness. Joints’ aperture is less than one millimetre (Access gallery report, 2013). The exposure and the surveying line are shown in Figure 2.


In Table 1, a summary of the surveyed joints is presented. Inability to record the joints with a length shorter than the measurement criterion have been considered as a truncation error. The joints, which are not observable due to the rock exposure limitations, have also been considered as censoring error (Ferrero and Umili, 2011). Decreasing the measurement level during joint surveying can minimize the effect of truncation error. In this study, 0.1 m length has been chosen as the measurement limit. The chosen rock exposures are also bigger than the existing joints. Thus, the truncation error is not considered seriously. Furthermore, the censoring errors can also be ignored in this investigation due to high percentage of the observable joints from both sides, R2 termination.
STATISTICAL ANALYSIS OF THE JOINTS GEOMETRICAL FEATURES
The data processing involves determining joint parameters, such as dip, spacing, persistence etc., stochastically based on its distribution function. Theoretically, a variety in the joint distribution functions stems from various mechanical processes that generate the joint; e.g. uniform stress distribution functions result in exponential distributions and complex processes result in lognormal distributions (Dershowitz and Einstein, 1988). The appropriate data required for statistical studies can be obtained from discriminating each set and specifying its related features such as dip, dip direction, spacing and persistence. Based on the dip and dip direction of the surveyed joints from the right bank of dam, as shown in Figure 3, four sets of joints have been discovered in this area.

Orientation distribution
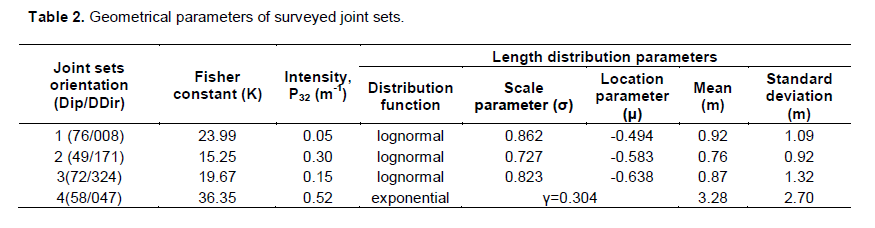
Joint orientation has two components: dip and dip direction. It has been shown that dip direction follows uniform distribution and dip angle follows Fischer distribution (Xu and Dowd, 2010). Fischer constant, for each joint set, has been obtained from Dips software and is shown in Table 2.
Joint intensity
Rock joint intensity is a measurement of the number of joints in the rock mass units such as volume, area or length. Joint intensity in two dimensions, P21, is defined as the overall length of the joints inside the given area. The three-dimensional parameter of joint intensity, P32, is defined as the overall area of the joint plane in the volume unit. Like P21, this parameter is both scale- and orientation- independent as a volume parameter (Dershowitz and Herda, 1992).
Volumetric joint intensity (square meters/cubic meters), P32, can be obtained from the surveyed surface joint intensity (meter/square meters). Zhang and Einstein (2000) proposed the following equation to calculate P32:

Here, the number of joints has been counted by one square meter framework with ten square centimetres meshed networks (Figure 4). The joints crossing each meshed line were counted and the total number of the counted joints in the one square meter framework was defined as the surface joint intensity (Lin and Yamashita, 2013). Through the use of the field measurements and with the use of Equation 2, the amounts of P32 were calculated separately for each joint set (Table 2).

Spacing distribution
Spacing is defined as the space between two adjacent discontinuities along the survey line. Based on the field measurements, spacing distribution of the discontinuities for different types of sedimentary, igneous and metamorphic rocks can be modelled with negative exponential probability density distribution function (Baecher, 1983; La Pointe and Hudson, 1985). Furthermore, it has been proved that if the joint locations are stochastic, probability density distribution function of the joint spacing would be negative exponential (Priest, 1993). Therefore, in this article, negative exponential distribution has been used for spacing.
Persistence distribution
Joint trace length, which is a result of the joint coincidence with the exposure surface, indicates the expansion of joint plane and determines the size of the rock blocks (Sari, 2009). As mentioned, direct surveying of the discontinuities inside the rock is impossible; thus a few studies regarding the three-dimensional joint surveying have been performed. Therefore, practically, it is supposed that the three-dimensional joints measurements have statistical features similar to the results obtained from the two-dimensional surveying (Xu and Dowd, 2010). Usually, for distribution of joint trace length, three functions of negative exponential (Baecher, 1983; Kulatilake et al., 2003), lognormal (Priest, 1993; Zhang and Einstein, 2000; Zadhesh et al., 2013) and Gama (Priest, 1993; Zhang and Einstein, 2000) are used which can be obtained from the two dimensional joint surveying.
The goodness-of-fit (GOF) tests measure the compatibility of a random sample with a theoretical probability distribution function. In this paper, three goodness of fit tests; Kolmogorov-Smirnov test, Anderson-Darling test and Chi-Squared test were used to evaluate probability distribution of the rock joint trace length. With regard to the previous investigations, GOF tests statistics were calculated for lognormal, Gamma and exponential distribution functions separately. Comparison results of the GOF tests statistic value are shown in Figure 5.
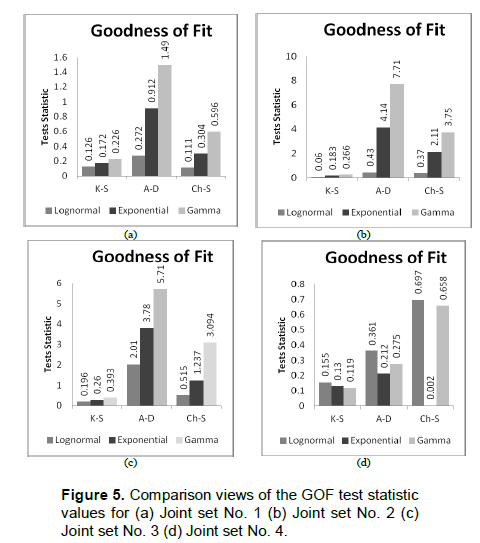
According to calculated GOF tests statistics, the lognormal probability distribution function, defined below, was found to be the best probability distribution function for representing a trace length distribution of joint sets number 1, 2 and 3.

GEOMETRICAL-STOCHASTICAL MODEL BUILDING AND VALIDATION
In stochastic modeling, the general approach is to treat locations, persistence (size), orientation and other properties of the joints as random variables with inferred probability distributions. These distributions supply the basis of the stochastic occurrence. When modeling, the joints are grouped in joint sets which are identified from the statistics of the measured data and the geologic history of the region. Model building is started with generation of joint set planes. Each set is modeled separately and the final simulation is the simple combination of all independently simulated sets. If no data on joint hierarchy is available or there is no evidence of joint hierarchy, as occurred here, then the choice is made randomly, effectively mimicking a random joint hierarchy.
In model building, joint production inside the model continues until the number of the joints crossing the borehole or surveying surface is reproduced. The joint intensity is controlled in the model through direct comparison of the observed and stimulated joints.
In the developed computer code FRAC3D, a fracture set is characterized by five following parameters:
a) Fractures center location.
b) Probability density function (PDF) of variation of fracture plane orientations including uniform, partial uniform and Fisher.
c) Mean orientation of fracture set.
d) Fracture intensity.
e) PDF of variation of fracture plane persistence including lognormal, Gamma and exponential distribution functions.
In the FRAC3D, the joints are convex polygonal planar objects of discontinuous rock, randomly oriented and located in three dimensional spaces. The FRAC3D incorporates Poisson plane and line stochastic processes. A joint set is generated by applying a sequence of four stochastic processes in space:
- First process: Create a homogeneous Poisson network of planes in space.
- Second process: Subdivide each plane into a jointed region and its complementary region of intact rock by a homogeneous Poisson line network.
- Third process: Mark created polygons in previous step based on shape and size.
- Fourth process: Shift the polygons, that have been marked as jointed, in the vicinity of their original position randomly.
It should be noticed that a fracture system, including joint sets, is generated with reiteration of presented processes. The first two processes constitute essentially the probabilistic model proposed by Veneziano (1978). The third process in which the joint areas and the complementary intact rock areas are marked as heterogeneous. Through the use of the fourth process, co-planarity feature of the joints can be considered. These two features differentiate between the model presented in this paper and the one presented by Veneziano. This model produces joint sets with specific variation of shape and size. Therefore the new model provides a more realistic representation of the natural rock joint systems.
In the FRAC3D, polygons with shapes similar to the shapes of natural fractures are remained. A polygon has a suitable shape and is considered as a fracture if it has the following conditions: a) the polygon has at least four vertices; b) all angles are at least 60°, and c) the polygon elongation is not more than permitted value. A polygon is retained with probability P=1.0 if it has an appropriate shape, and discarded otherwise.
Furthermore, joint sizes are fitted on a specific distribution such as negative exponential, lognormal or Gama. The method used for modelling the various distributions is shown described below. In each interval, polygons remain as joints with a Pf probability. In other words, polygons with a 1-Pf probability are omitted, that is, the difference between the desired PDF of the joint sizes (that is, lognormal, exponential or Gama) and the PDF of the good polygon sizes. The amount of the Pf probability is defined by the desired PDF. If the interval (a, b) is a subdivision of the range of continuous random variable, X, then:
Where, Fx is the cumulative distribution function of random variable, X.
It must be noted that in the current model, parts of the polygons (good polygons) are chosen as joints based on the criteria of the appropriate shape of the joint. Gama PDF with α=0.51 and β=1.96 is fitted on the sizes of these good polygons. This distribution presents the natural joints systems in which there are a few large joints and a lot of small joints. Then, each good polygon is controlled based on the desired PDF fitting.
In Figure 7, simulation of the rock mass joint networks of the right bank of Lorestan Roodbar dam is shown based on the developed three-dimensional stochastic model and the use of the geometrical parameters presented in Table 2. This simulated joint network shows 45297 joints in an area with 30×30×30 m3 size.
Figure 8 shows the joint traces obtained from the joint networks generation on a vertical square window of size 30 m having the strike direction same as the trend direction of the scanline (340°) and placed at the middle of the 30 m cube. A 20 m length of scanline is simulated in Figure 8. The 1-D joint frequency on this simulated scanline is about 1.9 joints per m. This value compares quite well with the observed 1-D joint frequency of 2.2 joints per m on actual scanline. This findings show that the joint geometry features of the generated fracture system agree well with the joint data used to model the 3-D stochastic joint networks.
The most important step in rock mass analysis is to present a precise definition of the discontinuities network (creating a geometrical model). In this paper, three-dimensional geometrical model of joint networks in the right bank of Lorestan Roodbar dam plant is prepared through the use of the developed stochastic model. In this model, by using a new method, the produced joints match the desired probability density function of the joint persistence. In addition, a computer program written in C++ language, called FRAC3D, which has the ability to produce the text and graphical output of the joint network, is developed for the purpose of implementing the model. Using statistical studies on the geometrical features of the existing joint sets in considered case study, the required inputs for the computer program have been provided. The current model can be very useful for studying the mechanical and hydraulic behaviour in this area.
The authors have not declared any conflict of interests.
REFERENCES
Baecher GB (1983). Statistical analysis of rock mass fracturing. J. Math. Geol. 15(2):329-347.
Crossref |
|
|
Baghbanan A, Jing L (2008). Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci., 44: 704-719.
Crossref |
|
|
Bang SH, Jeon S, Kwon S (2012). Modeling the hydraulic characteristics of a fractured rock mass with correlated fracture length and aperture: application in the underground research tunnel at Kaeri. Nucl. Eng. Tech. 44(6): 639-652.
Crossref |
|
|
Dershowitz WS, Einstein HH (1988). Characterizing rock joint geometry with joint system models. Rock Mech. Rock Eng. 21: 21-51.
Crossref |
|
|
|
Dershowitz WS, Herda HH (1992). Interpretation of fracture spacing and intensity. 33th US Symposium on Rock Mechanics, Rotterdam, Balkema, pp. 757-766. |
|
|
Ferrero AM, Umili G (2011). Comparison of methods for estimating fracture size and intensity applied to Aiguille Marbre´e (Mont Blanc). Int. J. Rock Mech. Min. Sci. 48(8): 1262-1270.
Crossref |
|
|
|
Flynn ZN, Pine RJ (2007). Fracture characterization determined by numerical modeling analyses. 11th Congress of the international Society for Rock Mechanics - Ribeiro e Sousa, (Olalla & Grossmann Ed.), Taylor & Francis Group, London, ISBN 978-0-415-45084-3 |
|
|
|
Ford NT, Pine RJ, Flynn ZN (2007). Discrete fracture network modelling and characterisation of rock masses for block caving design, 11th Congress of the international Society for Rock Mechanics - Ribeiro e Sousa, (Olalla & Grossmann Ed.), Taylor & Francis Group, London, ISBN 978-0-415-45084-3 |
|
|
|
Hudson JA, Harrison JP (1997). Engineering rock mechanics: an introduction to the principles. 1st ed. Tarrytown, N Y: Pergamon. |
|
|
Hudson JA, La Pointe (1980). Printed circuits for studying rock mass permeability. Int. J. Rock Mech. Min. Sci. Geomech. Abs. Techn. Note 17(5): 297-301.
Crossref |
|
|
|
Ivanova V, Xiaomeng Y, Veneziano D, Einstein HH (1995). Development of stochastic models for fracture systems. 35th U.S. Symposium on Rock Mechanics (USRMS), Reno, Nevada. |
|
|
Kulatilake PHSW, Park J, Um J (2004). Estimation of rock mass strength and deformability in 3-D for a 30 m cube at a depth of 485 m at Aspo Hard Rock Laboratory. Geotech. Geol. Eng. 22(3): 313-330.
Crossref |
|
|
Kulatilake PHSW, Um J, Wang M, Escandon RF, Varvaiz J (2003). Stochastic fracture geometry modeling in 3-D including validations for a part of Arrowhead East Tunnel, California, USA. Eng. Geol. 70(1): 131-155.
Crossref |
|
|
La Pointe PR, Hudson JA (1985). Characterization and interpretation of rock mass jointing patterns. Geol. Soc. Am. Spec. Pap. pp. 1-37.
Crossref |
|
|
Lin A, Yamashita K (2013). Spatial variations in damage zone width along strike-slip faults: An example from active faults in southwest Japan. J. Struct. Geol. 57: 1-15.
Crossref |
|
|
|
Martel S, Hestir K, Long JCS (1991). Generation of fracture patterns using self-similar function concepts. Earth Sciences Division Annual Report, Lawrence Berkeley Lab, Berkeley, CA, 52-56. |
|
|
Priest SD (1993). Discontinuity Analysis for Rock Engineering. Published by Chapman & Hall, London.
Crossref |
|
|
|
Priest SD, Samaniego JA (1988). The statistical analysis of rigid block stability in jointed rock masses. 5th Australia-New Zealand Conference on Geomachanics, The Institution of Engineers Australia, Sydney, pp. 398-403. |
|
|
|
Reyes O, Einstein HH (1991). Failure mechanics of fractured rock - A fracture coalescence model. 7th Congress of the international Society for Rock Mechanics, Aachen, Germany. |
|
|
Robinson PC (1983). Connectivity of fracture systems - a percolation theory approach. J. Phys A: Math. Gen. 16: 605-614.
Crossref |
|
|
Sari M (2009). The stochastic assessment of strength and deformability characteristics for apyroclastic rock mass. Int. J. Rock Mech. Min. Sci. 46(3): 613-628.
Crossref |
|
|
|
Secondly Engineering Geology Report (2007). Rudbar Lorestan Dam & Hydropower Plant, Iran Water & Power Resources development Co. |
|
|
|
Study on Possibility of Concrete Lining Omission in AGC (Access Gallery) Report (2013). Rudbar Lorestan Dam & Hydropower Plant, PÙyry Energy Ltd., Iran Water & Power Resources development Co. |
|
|
|
Veneziano D (1978). Probabilistic models of joints in rock. Research report, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA. |
|
|
Xu C, Dowd P (2010). A new computer code for discrete fracture network modeling. Comput. Geosci. 36(3): 292–301.
Crossref |
|
|
|
Yu X (1992). Stochastic modeling of rock fracture geometry. M.S. Thesis, MIT, Cambridge, MA. |
|
|
Zadhesh J, Jalali SE, Ramezanzadeh A (2013). Estimation of joint trace length probability distribution function in igneous, sedimentary, and metamorphic rocks. Arab. J. Geo. Sci.
Crossref |
|
|
Zhang L, Einstein HH (2000). Estimating the Intensity of Rock Discontinuities. Int. J. Rock Mech. Min. Sci. 37(5): 819-837.
Crossref |