ABSTRACT
In the Niger Delta, low oil recovery rates less than 30% results mainly due to oil production problems such as water coning, wax deposition and high gas/oil ratios. Meanwhile, the remaining oil becomes a good candidate for EOR methods such as CO2 injection, polymer and foam injection, in-situ combustion and steam injection. But as it stands, the practice of these known methods of enhanced oil recovery is scarce in the Nigeria’s Oil and Gas industry. However, this project is aimed at evaluating the application of foam injection as an enhanced oil recovery method in sandstone reservoir and exploring possible improvement of oil production in the Niger Delta. The project was carried out using two cases. In Case 1, a synthetic model built with static modeling software, later imported to dynamic modeling software and simulated to mimic foam injection process while in Case 2 a real life model with an aquifer fully populated with the necessary reservoir and fluid properties and production history. From the results obtained in Case 1, production indices, field oil recovery, etc. were compared with gas flooding process. For foam flooding, a significant increase in oil recovery as compared to gas flooding and reduction in gas oil ratio and gas produced were observed while in Case 2, field oil recovery, oil production rate, cumulative oil production, gas oil ratio and water cut were compared and significant increase oil recovery using foam flooding, and reduced field water cut was also observed. The economic viability of the project in both cases was also investigated using some economic indicators. Improved displacement efficiency resulting into increased recoverable reserves, and subsequently increased total field oil production has been achieved by foam injection.
Key words: Chemical, foam, enhanced oil recovery, modeling, oil production.
Foam is a colloidal dispersion in which a gas is dispersed in a continuous liquid phase. Surfactants are added to the solution to stabilize foam by reducing interfacial tension. The use of surfactant solutions that increase oil recovery has been deeply studied. In the sixties it was proposed to use foams instead of just aqueous surfactant solutions as displacement agents. The first experiments showed that oil from porous structures unrecoverable by conventional water or gas drives could be displaced by foam. The efficiency of the foam was believed to be the result of the high foam viscosity (apparent viscosity) and its penetration in pores of various sizes. Laboratory research has indicated that the foam-drive process can recover a significant proportion of the oil remaining in unconsolidated sand packs subjected to conventional secondary recovery operations. Exerowa and Kruglyakov (1998) reported that researchers experimented with crude oils and unconsolidated porous media, indicating that total recovery increased from 60% (from water flooding) to 90% after foam injection using 36 foaming agents (23 anionic, 6 non-ionic and 7 amphoteric) to establish the effect of foam quality (gas volume fraction), the surfactant kind and concentration, the mode of the foam injection and the foam bank size on the displacement ability of the foam. The main point of these experiments was that the oil recovery changed with the quality of foam and the permeability.
Yan et al. (2006) investigated different factors’ effects on sweep efficiency by foam in smooth heterogeneous fractures and applied their theory to that situation assuming the same gas fractional flow in each portion of the fracture and no cross-flow. Their study was based on the fact that foam can reduce viscous fingering and gravity override caused by the low viscosity and density of the gas.
They consider foam to improve efficiency of a surfactant process for oil recovery in a reservoir consisting of multiple fractures separating matrix blocks where oil is retained by capillarity and/or wettability. Yan et al. (2006) concluded that foam can greatly improve the sweep efficiency in a heterogeneous fracture system.
Sweep efficiencies can be affected by gas fractional flow, aperture ratio and bubble size. The use of foams to improve oil recovery has been used in lab scale and has been tested in real reservoirs, according with Blaker et al. (1999), and predictions based on laboratory experiments and simulations seem to match with results of real processes. Opportunities for research to deeply understand all the phenomena in foam processes as stated by Kovscek and Bertin (2002) are numerous.
The behavior of the foam in porous media is related to the connectivity and geometry of the rock. Porous media have several characteristics that are important to the flow of foam, like the size distribution of the pores and throats.
Foam mechanisms for generation and destruction of lamellae depend strongly on the body to size aspect radio. For large pores occupied mainly by the non-wetting fluid, the wetting fluid resides in the corners and in thin wetting films coating the pore walls. The non-wetting phase resides in the central portion of these large pores. Small pores are filled with wetting fluid. Then the wetting phase remains continuous. During two-phase flow, the non-wetting fluid flows in interconnected large pore channels, while wetting fluid flows in interconnected small channels and in corners of non-wetting phase occupied pores because of pressure gradients in the wetting phase.
Bulk foam is present when the length scale confining the fluids is greater than the length scale of the bubbles, and can be classified as “kugelschaum” (that is, ball foam) and “polyderchaum” (that is, polyhedral foam). In the first category, spherical bubbles well separated conform the foam, and in the second category the bubbles are separated by thin films or lamellae. When the foam flows in porous media, bubbles and lamellae span completely across the porous space and are called confined foam according to Radke and Gillis (1990).
When the characteristic pore size is comparable to or less than the characteristic size of dispersed gas bubbles, the bubbles and lamellae span pores completely. At low gas fractional flow, the pore spanning bubbles are widely spaced, separated by thick wetting liquid lenses or bridges. At high gas fraction flow, the pore spanning bubbles is in direct, contact, separated by lamellae. Hirasaki and Lawson (1985) denoted this direct contact morphology as the individual lamellae regime.
Although both bulk foam and individual lamellae foam can exist in principle, effluent bubble sizes equal to or larger than pore dimensions are usually reported. It is generally accepted that single bubbles and lamellae span the pore space of most porous media undergoing foam flow in the absence of fractures.
Figure 1 shows the schematic of foam in porous media. The gas can be trapped or flowing as a continuous or discontinuous phase. In discontinuous gas foam, the entire gas phase is made discontinuous by lamellae, and no gas channels are continuous over sample spanning dimensions. Gas is encapsulated in small packets or bubbles by surfactant stabilized aqueous films. In continuous gas foam, the media contain some interconnected gas channels that are interrupted by lamellae over macroscopic distances much greater than pore dimensions.
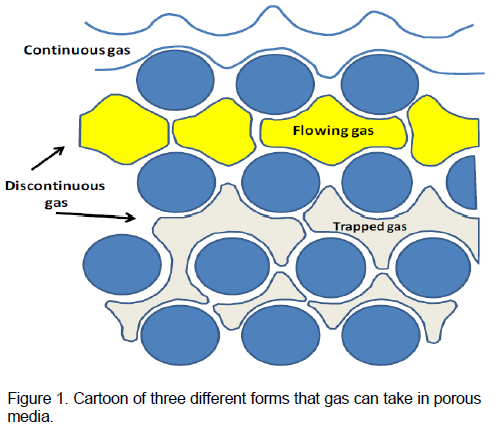
Discontinuous foam forms under co-injection of gas and surfactant solution, provided that the wetting phase saturation and flow rate are high enough for foam generation. When the wetting phase saturation is low enough, the lamellae generation rate may become lower than the rupture rate, and paths of continuous gas flow may result. Figure 1 is also a summary of the pore level microstructure of foam during flow through porous media. Because of the dominance of capillary forces, wetting surfactant solution flows as a separate phase in the small pore spaces. A minimal amount of wetting liquid transports as lamellae. So the wetting phase relative permeability is unchanged when foam is present. When both flowing and trapped gas exist, flowing foam occurs in large pores because the resistance there is less than in the smaller pores. Then bubble trapping can happen only in intermediate sized pores.
Thus, foam can be classified into “weak” foam and “strong” foam. For “weak foam” with no moving lamellae, the increase in trapped gas saturation is important to the behavior of foam flow as it results in the blockage of gas pathways, which reduces the relative permeability of gas.
The trapped gas reduces mobility, but the rest of gas flows as continuous gas.
“Strong” foam flows by a different mechanism. The lamellae make the flowing gas discontinuous. Then the bubbles trains face much higher resistance than in continuous gas flow. The apparent viscosity of the discontinuous foam is much greater than in continuous foam. The combined effect of the reduction of gas relative permeability and the increase of apparent gas viscosity greatly increases the mobility reduction effect of foam.
The most important factors that affect foam trapping and mobilization are pressure gradient, gas velocity, pore geometry, bubble size, and bubble train length. Increasing the pressure gradient can open new channels which were occupied by trapped gas.
Statement of problem, objective and limitation of study
The major objective of this study is to evaluate the application of foam injection as an enhanced oil recovery method in sandstone reservoirs and exploring possible improvement of oil production in the Niger Delta (Figure 2), since foam can help reduce gas mobility and affect the oil recovery in three ways:
1. By stabilizing the displacement process as the displacing fluid (gas) viscosity increases;
2. By blocking the high-permeable swept zones and diverting the fluid into the unswept zones; and
3. By reducing the capillary forces via reducing the interfacial tensions due to the presence of surfactant.
The evaluation of the application of foam injection as an enhanced oil recovery method in sandstone reservoir was carried out using two cases and will follow the steps listed as follows:
1. Obtaining a real life reservoir model/building a synthetic reservoir model;
2. Simulation of the foam injection process;
3. Comparison of results (such as production indices, field oil recovery and so on) for foam injection with gas flooding/water flooding.
Generally, water /gas flood efficiency in sandstone reservoirs is relatively low, due to heterogeneity. In the case of gas flooding, major problems that are usually encountered are poor volumetric sweep efficiency and low incremental oil recovery due to channeling or fingering and gravity segregation, which are caused by rock heterogeneity as well as the low density and viscosity of the injected gas. The need for mobility control in gas flooding has led to the use of foam for sweep improvement and profile modification. Foam is employed to improve the efficiency by which the displacing fluid sweeps the reservoir and contacts and recovers oil. Limitations are:
1. The ECLIPSE Foam model does not attempt to model the details of foam generation and collapse.
2. Detailed laboratory studies (pilot test) need to be done before implementation of foam flooding.
3. There are very few real reservoir models to be used for carrying out the study.
5. Foam is modeled as tracer which may be transported with either the gas or the water phase with account taken of adsorption on to the rock surface and decay over time.
Foams in porous media
Gas injection for enhanced oil recovery can be efficient at mobilizing oil where gas sweeps, but suffers from poor volumetric sweep efficiency because of reservoir heterogeneity, viscous instability and gravity segregation of injection gas to the top of the formation (Lake, 1989). Foam can address all three sources of poor sweep of gas (Schramm, 1994; Rossen, 1996).
Foam is a dispersion of gas in liquid (Bickerman, 1973). The dispersed phase is sometimes referred as the internal or discontinuous phase, and the liquid phase as the external or continuous phase. In foam, gas bubbles are separated by thin film of fluid called lamella. The lamella surrounding gas bubbles are normally unstable and break very quickly. However, the presence of surface active agents (surfactants) stabilizes the lamellae, thus improving foam stability.
Foam generation mechanisms inside a realistic porous media
Snap off: Roof (1970) showed that when oil emerges from a water-wet constriction into a water filled pore, the interfacial forces are such that a leading portion of the oil may separate into a droplet (snap off). The same mechanism occurs during invasion of gas to pores filled with liquid. It takes place regardless of the presence or absence of surfactant, but if a stabilizing surfactant is not present, snapped off bubbles quickly coalesce (Kovscek and Radke, 1993). The snap-off process is a result of the difference in the capillary pressure between the pore body and pore throat. Thus occurrence of the process is a function of ratio of the body-to-throat equivalent diameters. Kovscek and Radke (1993) and Li et al. (2010) presented details of the snap-off process.
Leave behind: The leave behind mechanism also occurs during invasion of a gas phase to a porous medium saturated with a liquid phase. Foams generated solely by leave-behind give approximately a five-fold reduction in steady-state gas permeability (Ransohoff and Radke, 1988; Kovscek and Radke, 1993), whereas discontinuous-gas foam created by snap-off resulted in a several-hundred fold reduction in gas mobility (Persoff et al., 1991; Ettinger and Radke, 1992; Kovscek and Radke, 1993). This indicates that the strength of foam (that is, number and stability of lamellae) is affected by the dominant mechanism of foam generation.
Lamella division mechanism: Increasing number of lamellae or bubbles by lamella division mechanism can be existed when mobile foam bubbles are pre-existed in the porous medium. When a moving lamella train encounters a branch in the flow path, it may split into two, one in each branch of the path (Tanzil et al., 2002). Lamella division is thought to be the primary foam-generation mechanism in steady gas-liquid flow (Gauglitz et al., 2002; Li, 2006).
Flow characteristics of foam in porous media
In porous media, foam flow is characterized by the location of wetting and non-wetting phases in pores. The non-wetting phase resides in the central portion of the large pores, while wetting phase resides in corner of the gas-occupied pores and in thin wetting films coating the pore walls.
During the flow of foam in porous media, gas can be trapped, or flowing as a continuous or discontinuous phase. In continuous-gas flow, the porous media contains some channels uninterrupted by lamella. In discontinuous-gas flow, the entire gas phase is made discontinuous by lamellae, and no gas channels are continuous over macroscopic distances. Discontinuous foam is usually associated with stronger foam strength. All three types of channels can be present in the porous medium during foam flow.
This study was carried out using two cases with one being a synthetic model and the second one being a real model.
Case 1
This case entails building a synthetic model using a static modelling software and populating the model with average petrophysical properties, pressure, volume, and temperature properties, as well as saturation dependent data unique to unconsolidated sandstone as generated using relevant correlations. The model will then be imported to dynamic modeling software and simulated to mimic foam injection process.
Case 2
As regards this case, the real life model was obtained, it is a case in which the static model had already been built with an aquifer and simulated using dynamic software to mimic water flooding process. This case therefore, entails importing the already built static model to dynamic modeling software for simulation to mimic foam injection.
An economic analysis was run to check for the viability and possible implementation of the project.
Building a simple synthetic model
A synthetic model is an artificial 3-D reservoir model whose surface and horizons are created using artificial algorithm. This 3-D model incorporates all the geologic attributes of the reservoir to be built. These attributes include the structural shape and thicknesses of the formations within the subsurface volume being modeled, their lithology, and the porosity and permeability distributions.
The static model as shown in Figure 3 (synthetic) was developed using Petrel; static modelling software.
Steps to building a synthetic model are:
1. Creation of grided surfaces: Anticlinal surfaces were created and served as input data required for the creation of a 3-D grided dome-like structure.
2. Making horizons from created surfaces: The created surfaces were converted into horizons as soon as they were made to form a 3-D grid.
3. Making zones from created horizons: Zones are geological portion in the Stratigraphic intervals above, in-between and below the horizons. This process defines the sub units of the 3D grid and is carried out in the “make zone” section. It inserts additional horizons and zones into the 3D grid by inserting isochores up or down from the previously input horizons. The model was divided into three zones by four horizons.
4. Layering: This is the final step; it involves making the final vertical resolution of the 3D grid and this is done by dividing each zone into layers. The model was divided into nine layers.
There are nine layers in the model, which are grouped into three zones. The first three red layers makes up the first zone, the next three purple layers makes up the second zone, while the last three blue layers makes up the third zone.
Making zones from created horizons: Zones are geological portions in the Stratigraphic intervals above, in-between and below the horizons. This process defines the sub units of the 3D grid and is carried out in the “make zone” section. It inserts additional horizons and zones into the 3D grid by inserting isochores up or down from the previously input horizons. The model was divided into three zones by four horizons.
Layering: This is the final step; it involves making the final vertical resolution of the 3D grid and this is done by dividing each zone into layers. The model was divided into nine layers (that is, each zone was divided into three layers).
The reservoir model is a 30 by 30 by 9 model and was discretized into 8100 cells. With the aid of the property calculator the model was populated with some petrophysical properties. Using arithmetic averaging (random distribution), average porosity of 27% was assigned the cells. Arithmetic averaging was used for populating porosity because we assume isotropic nature of the property. While triangular distribution was used in populating the permeability of the reservoir with the minimum, medium and maximum values being 300, 1000 and 1700 md respectively. Triangular distribution was used to populate the permeability because of the anisotropic nature of the property. A net to gross ratio of 0.8 was used to describe proportion of the gross rock volume formed by the reservoir rock.
For this study, investigation was done for an undersaturated reservoir and light oil fluid model was used. Since there is no compositional variation with temperature and pressure of the reservoir fluid, a black oil simulator (ECLIPSE 100) was used to simulate the process.
Reservoir simulation basics can be summarized in these steps:
Divide the reservoir into several cells:
Case 1: In the case of the synthetic model, this step has been carried out in the static modelling software and can be imported into the dynamic modelling software (ECLIPSE 100) using an INCLUDE file keyword. Figure 4 is the reservoir model showing the location of wells (Case 1)
Case 2: The reservoir model in this case is a real one. This implies that the model has been built already all it needs is for it to be imported to the dynamic modelling software for simulation. Figure 5 is the reservoir model showing the location of wells (Case 2).
Provide basic data for each cell:
1. Fluid and rock properties: The PVT data are used to translate produced volumes to reservoir conditions and to convert these to mass, ready for the simulator's mass balance equations. PVT tables are derived from a combination of laboratory experiments, field tests or correlations.
The PVT properties of the reservoir model in Case 1 such as solution gas oil ratio, formation volume factor and viscosity were defined using correlations. The reservoir fluid data are needed to evaluate phase density at reservoir and stock tank conditions.
Case 1: the reservoir pressure is 3814.7 psi (26 301.4 kpa) at 7100 ft (2164 m) and reservoir thickness of 400 ft (122 m) with gas/oil contact of 7100 ft (2164 m) and oil/water contact of 7450 ft (2271 m).
Case 2: The PVT data for this reservoir is as specified in the already built model. The reservoir pressure is 3035.7 psi (20 930 kpa) at 7000 ft (2134 m) with gas oil contact of 7000 ft (2134 m) and oil water contact of 8200 ft (2499 m).
Petrophysical data:
Case 1: The rock compressibility data for unconsolidated sandstone was generated using Newman’s correlation and also the saturation dependent data were also generated for sandstone using relevant correlations.
Case 2: Average porosity is 18%, average permeability is 308md, while other data such as rock compressibility data and saturation dependent data are as specified in the already built model.
Positioning/completion of wells within the cells
Case 1: A total of eleven wells were drilled; consisting of three gas injectors and ten producing wells. The gas injectors were located at the crest of the structure while the producers were located at the flanks of the reservoir. The producers were perforated at layers 3 to 7, while the gas injectors were perforated at layers 1 to 3 so as to efficiently push the oil towards the perforations. The gas injectors will be used to inject the surfactant into the reservoir.
Case 2: A total of seven wells were drilled; consisting of three gas injectors and ten producing wells. With four producers and one gas injector located on the center fault block of the structure while the last producer and the second injector were located on the west fault block of the reservoir as shown in Figure 5. The producers (1, 2, 3, 4) were perforated at layers 1 to 12, 1 to 10, 2 to 9 and 1 to 3 respectively while the gas injector was perforated at layers 1 to 4 (on the central fault block) so as to efficiently push the oil towards the perforations while the producer and injector on the west fault block were perforated at layers 1 to 10 and 1 to 4 respectively. The gas injectors will be used to inject the surfactant into the reservoir:
1. Specify well production rates as a function of time. The well production rates are controlled using the required keywords
2. Solve equations to yield the pressure and saturation for each block, as well as production of each phase from each well
Each cell is solved simultaneously, so the number of cells in the simulation model is directly related to the time required to solve a time step. In general, short time steps are easier (quicker) to solve than long ones.
The distribution of the injected foam is solved by a conservation equation: as a tracer in the gas phase with decay, or as a tracer in the water phase with decay (Equations 1 and 2 respectively):
Modeling foam injection in reservoir using eclipse
Foam flooding through the reservoir can be modeled using the ECLIPSE 100 simulator. The ECLIPSE Foam model does not attempt to model the details of foam generation and collapse. Foam is modeled as tracer which may be transported with either the gas or the water phase with account taken of adsorption on to the rock surface and decay over time.
Case 1
A 30 by 30 by 9 model consisting of 8100 cells was used. The reservoir model was simulated using ECLIPSE black oil simulator E100 due to the constant composition of the reservoir fluid with respect to temperature and pressure. The reservoir is an undersaturated reservoir as the reservoir pressure is greater than the bubble point pressure. Upon initialization, the oil in place was discovered to be 2402MMSTB while the dissolved gas was 1806BSCF.
In exploiting the reserve, a total of 11 wells was proposed consisting of 3 gas injectors and eight producers. The gas injectors would be used for co-injection of surfactant and gas into the formation. The simulation was carried out to mimic foam injection for a period of sixty four years starting September 2013 and the rate of production was maintained at 150,000STB/D.
Case 2
A 24 by 25 by 12 model consisting of 7200 cells was used. The reservoir model was simulated using ECLIPSE black oil simulator E100 due to the constant composition of the reservoir fluid with respect to temperature and pressure. The reservoir is an undersaturated reservoir as the reservoir pressure is greater than the bubble point pressure. Upon initialization, the oil in place was discovered to be 260MMSTB while the dissolved gas was 252BSCF.
In exploiting the reserve, a total of 7 wells was proposed consisting of 2 gas injectors and five producers. The gas injectors would be used for co-injection of surfactant and gas into the formation. The simulation was carried out to mimic foam injection for a period of sixty four years starting January, 1988 and the rate of production was maintained at 15,000STB/D.
Economics
In evaluating the economic viability of this project, economic indicators (yard stick) that will be used are the net present values (NPV) and the discounted profit to investment ratio. In all the cases that are to be considered, some of the economic data input will be assumed and sensitivity analysis will be adopted such that the views of a pessimist, optimist and inbetweenist will be portrayed and how their view affects the economics of the projects.
Case 1
In this case, results obtained for foam injection was compared with that gas injection (that is, without foam). The results include a plot of field oil recovery, field oil production rate, gas/oil ratio and field oil production total.
From the plot of the field oil recovery obtained (Figure 6), it can be seen clearly that the recovery factor for foam injection is about 62% while that of gas injection is about 46%, thus, showing an incremental recovery of 16% which is quite significant.
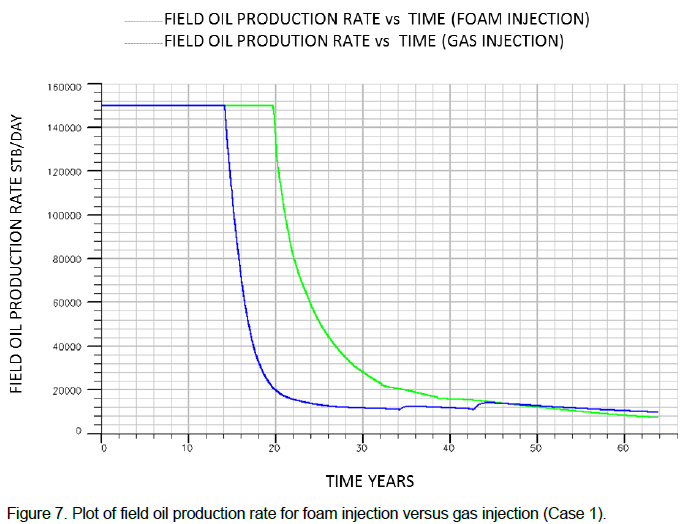
From the plot of the field oil production rate obtained (Figure 7), for foam injection the restricted production rate (150,000 STB/D) was maintained for about twenty years before the decline in production rate while for gas injection the restricted production rate (150,000 STB/D) was maintained for about fourteen years before production started declining. This implies that the foam injected was able to sustain the reservoir pressure above the pressure at which the production target will no longer be met, for a longer period of time as compared to when gas was injected.
From the plot of the field gas oil ratio obtained (Figure 8), a significant reduction in gas oil ratio was noticed with foam injection confirming the mobility reduction effect that foam has on gas. It shows that foam injection successfully delayed gas breakthrough/gas channeling (fingering) for over 40 years. For the gas injection without foam case, there was an increase in the field gas oil ratio once the reservoir crossed its bubble point.
Case 2
In this case, results obtained for foam injection was compared with that water injection. The results include a plot of field oil recovery, field oil production rate, field water cut and field oil production total.
Foam injection gave a total cumulative oil production of 1490 MMSTB while total oil production was 1106 MMSTB for gas injection (Figure 9). It can be inferred that foam injection enabled the optimization of recoverable reserve by squeezing out more oil from the reservoir compared to the gas injection.
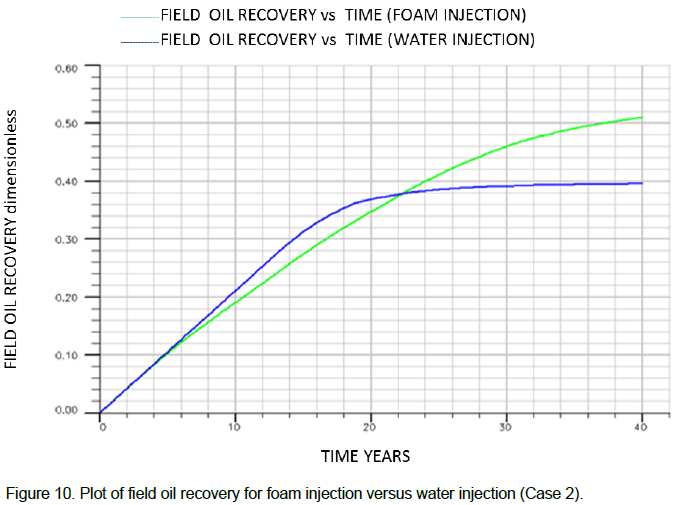
From the plot of the field oil recovery obtained (Figure 10), it can be seen clearly that the recovery factor for foam injection is about 51% while that of water injection is about 40%, thus, showing an incremental recovery of 11% which is quite significant.
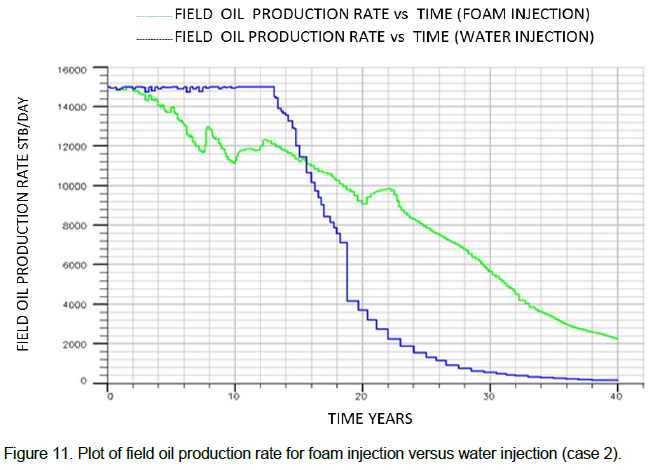
From the plot of the field oil production rate obtained (Figure 11), the quick commencement of the decline in production can be attributed to the fact that foam decays faster in the presence of oil and water, thus reducing the strength of the foam which in turn affects the efficiency of the foam injected into the reservoir. It can also be deduced from the production profile that even though the decline for foam injection started earlier as compared to water injection, foam injection still squeezed more oil from the reservoir over time than water injection. A better profile and recovery will be obtained if water is injection is employed for about ten to thirteen years before foam injection is initiated.
From the plot of the field water cut obtained (Figure 12), a significant reduction in water cut was noticed with foam injection confirming the fact that foam has an excellent blocking effect. It tends to block the high permeable zones which could enhance quick water breakthrough, thus significantly reducing water cut. For the water injection case, there was an increase in the field water cut.
Foam injection gave a total cumulative oil production of 133 MMSTB while total oil production was 103 MMSTB for water injection. It can be inferred that foam injection enabled the optimization of recoverable reserve by squeezing out more oil from the reservoir compared to the water injection.
Economics
Reserves can be defined as estimated quantities of crude oil, natural gas, condensates, natural gas liquids and other related substances which are known to be recoverable and marketable from known accumulations using established technologies and operating conditions
under approved regulations.
From the definition of reserves giving above, it is worthy of note that the economics of a project is equally as important as the technical aspect of the project, because there is no point embarking on a project that is not profitable.
In the light of the foregoing, economic indicators such net present value (NPV) and discounted profit to investment ratio (DPI) were used to determine the economic viability of the project. The economic assumptions made in carrying out the analysis and the results are shown in Tables 1 to 4 while the plots of the cumulative discounted cash flow against time are shown in Figures 13 to 15.
For case 1 the economics for foam flooding proved (using NPV and DPI as yard stick) to be more viable than that of gas injection. For case 2 the result for foam flooding was not provided because the values obtained for NPV and DPI are negative (implying the project is not viable). This can attributed to the high influence of the Opex and the injection cost on the cash flow. Water flooding on the other hand proved to be more viable because of its higher early cash flow and lesser effect of injection cost.
From the results obtained, foam injection has shown clearly the possibility of increasing recoverable reserves, thus, total field oil production by improving the displacement efficiency and subsequently mobilizing more oil towards the producers. Foam injection therefore stands a great chance of helping to provide a means to increase Nigeria’s recoverable reserves and optimize the nation’s oil reserves.
Further studies should be carried out on the use of foam injection in Nigeria, owing to the fact that before this EOR method can be used pilot tests have to be carried out and also the need for series of laboratory tests, which will help in determining the foaming agents that will be suitable for use in the Niger Delta reservoirs.
Foam injection however provides a way of reducing Nigeria’s gas flaring to near zero thereby preserving the nation’s asset. Foam injection reduces gas mobility thereby reducing the production of unwanted gas thus preventing its flaring.
The authors have not declared any conflict of interest.
The authors would like to acknowledge the management of the Schlumberger Learning Centre of the University of Ibadan for allowing us to use ECLIPSE 100 and Petrel E&P suite of Software donated by Schlumberger for this study.
REFERENCES
Bickerman JJ (1973). Foams. New York: Springer-Verlag.
CrossRef |
|
|
|
|
Blaker T, Celius HK, Lie T, Martinsen HA, Rasmussen L, Vassenden F (1999). Foam for Gas Mobility Control in the Snorre Field: The FAWAG Project. SPE Annual Technical Conference and Exhibition, Houston, Texas.
CrossRef |
|
|
Ettinger RA, Radke CJ (1992). The Influence of Texture on Steady Foam Flow in Berea Sandstone. SPERE 7(1):83-90.
CrossRef |
|
|
|
Exerowa D, Kruglyakov PM (1998). Foam and Foam Films. Elsevier. |
|
|
Gauglitz PA, Friedmann F, Kam S I, Rossen WR (2002). Foam Generation in Homogeneous Porous Media. Chem. Eng. Sci. 57(19):4037-4052.
CrossRef |
|
|
Hirasaki GJ, Lawson JB (1985). Mechanisms of Foam Flow in Porous Media: Apparent Viscosity in Smooth Capillaries. SPE J. 25(2):176-190.
CrossRef |
|
|
|
Kovscek AR, Bertin HJ (2002). Estimation of Foam Mobility in Heterogeneous Porous Media. SPE/DOE 75181 Improved Oil Recovery Symposium, Tulsa, Oklahoma 17-20 April. |
|
|
|
Kovscek AR, Radke CJ (1993). Fundamentals of Foam Transport in Porous Media, in Foams in the Petroleum Industry. L.L. Schramm, Editor., American Chemical Society, Washington, D.C., pp. 115-163. |
|
|
|
Lake LW (1989). Enhanced Oil Recovery, Prentice Hall, Upper Saddle River, NJ. |
|
|
|
Li, Q. (2006) Foam Generation and Propagation in Homogeneous and Heterogeneous Porous Media. PhD Dissertation, University of Texas at Austin, USA. |
|
|
Li RF, Yan W, Liu S, Hirasaki GJ, Miller CA (2010). Foam Mobility Control for Surfactant Enhanced Oil Recovery. SPE J. 15(4) 1-15.
CrossRef |
|
|
Persoff P, Radke CJ, Pruess K, Benson SM, Witherspoon PA (1991). A Laboratory Investigation of Foam Flow in Sandstone at Elevated Pressure. SPERE (Aug.) pp. 185-192.
CrossRef |
|
|
|
Radke CJ, Gillis JV (1990). A Dual Gas Tracer Technique for Determining Trapped Gas Saturation During Steady Foam Flow in Porous Media SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana. |
|
|
|
Ransohoff TC, Radke CJ (1988). Mechanisms of Foam Generation in Glass-Bead Packs. SPERE (May), pp. 573-585. |
|
|
Roof JG (1970). Snap-Off of Oil Droplets in Water-wet Pores. SPE J. 10(1970):85-90.
CrossRef |
|
|
|
Rossen WR (1996). Foams in Enhanced Oil Recovery, In: Foams: Theory Measurement and Applications, R.K. Prud'homme and S. Khan (Eds), Marcel Dekker, New York City. |
|
|
|
Schramm LL (1994). Foams: Fundamentals and Applications in the Tanzil D, Hirasaki GJ, Miller CA (2002). Conditions for Foam Generation in Homogeneous Porous Media. SPE 75176 presented at the 2002 SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, 13-17 April. |
|
|
Petroleum Industry. American Chemical Society: Washington, D.C. (1994).
CrossRef |
|
|
|
Yan W, Miller C A, Hirasaki G J (2006). Foam Sweep in Fractures for Enhanced Oil Recovery. Colloids and Surfaces A: Physicochem. Eng. Aspects (282-283):348-359. |
