SRR structure consists of two concentric rings with slits to avoid continuous flow of current within the rings (Pendry et al., 1999). The proposed metamaterial structure is a modification of Pendry’s SRR structure which is equivalent to two SRRs connected back to back. It is a highly resonant structure that can reduce the usage of LCs and relax the cost. A SRR is just a small LC circuit comprising an inductance L and a capacitance C. The ring forms one winding of a coil (an inductance) and the ends of the ring form parallel plates of a capacitor, thus adding capacitance to the structure. Thus it is possible that the LC frequency could be increased or decreased by decreasing or increasing the net capacitance. In this work we are focused on estimating the resonant frequency of the structure using equivalent circuit model and thus demonstrating the negative refraction in the proposed metamaterial structure.

The structure of the proposed metamaterial structure is shown in the Figure 1. The split ring resonator (SRR) structure is printed on a dielectric substrate of thickness 0.9 mm and dielectric constant 5.7 (mica). Radius of the outer and inner ring of the SRR is 2.9 and 2.7 mm respectively. The length and width of the rectangular strip are taken as 5.4 and 0.2 mm, respectively.

 

 

The unit cell is simulated by high frequency structure simulator (HFSS) by using PEC and PMC boundary conditions. The PEC boundary conditions are applied to those surfaces which are perpendicular to incident electric field vector (Sharma et al., 2011a, b).

 

The results are measured over a frequency range of 13.5 to 16.5 GHz by EM solver Ansoft HFSS. The structure under investigation is placed in a waveguide with dimensions 7.8 × 7.8 × 13 mm as shown in Figure 1. The unit cells are combined to form linear 2D array topology (Figure 2) to obtain the resonant frequency of 14 GHz which is equal to the resonant frequency of unit cell.

 

 

Equivalent circuit model

 

A split ring resonator is a metamaterial structure that possesses negative permeability over a certain frequency band around its resonance frequency. Sufficiently accurate equivalent circuit models for a SRR structure can be used to determine the behavior of a SRR in a simple, fast and efficient way (Ziolkowski et al., 2009). When an equivalent circuit is available, a relationship between physical properties of the SRR structure and its frequency dependent transmission/reflection behavior can be established. The resonant frequency of SRR structure can be expressed as f? = 1/2πLC, where the equivalent capacitance C (Here C₁=C₂=C) and inductance L (and L₁=L₂=L) can be derived using constitutive equations and analytical expressions to calculate the resonant frequency from the various geometrical parameters of the SRR (Chen et al., 2006). Figure 3 shows the equivalent circuit  model  for the SRR.

 

 

 

 

Where A is the area of plates of the slits and d is the distance between the plates (gap width).

Here, we report the simulation results for SRR unit cell and arrays to demonstrate the existence of metamaterial property in the proposed structure. The resonance frequency of the unit cell using the geometrical and physical parameters specified earlier is estimated to be f?= 14.1 GHz from the equivalent circuit model approach. By the HFSS simulation, the resonance frequency obtained is 14 GHz by less than 5% error.

 

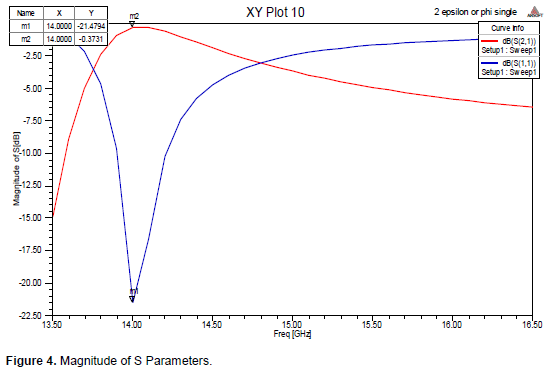
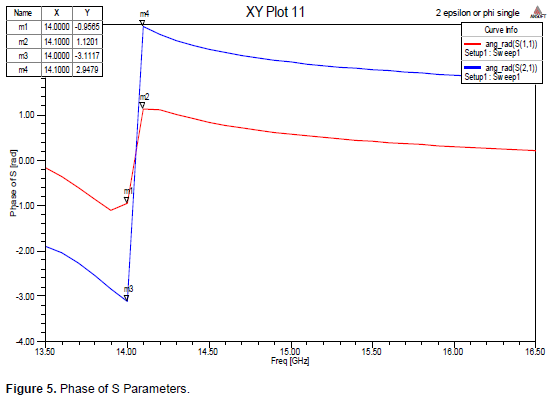
From the simulation results it is observed that the reflection coefficient, S₁₁ is showing a phase reversal at the resonance frequency thus indicating the existence of metamaterial property as shown in Figure 4. The transmission coefficient, S₂₁ is also observed in Figure 5. It is also found to show a phase reversal (zero crossing) at the resonance frequency which confirms the existence of the metamaterial property at this frequency. The magnitude and phase of S Parameters for SRR array computed by HFSS are shown in Figures 6 and 7 respectively. The array is assumed to be one-dimensional array extending along the y-direction and the coupling effects along this direction will be neglected. The SRR array resonates at f?= 14 GHz.

 

 

 

 

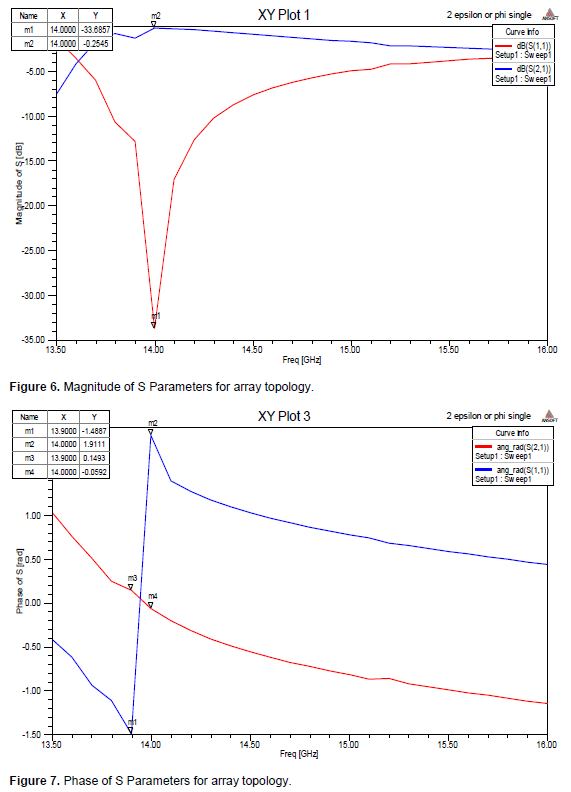
From Figures 6 and 7 it is clear that the array of metamaterial structure also shows the metamaterial properties. To show the physical properties of designed structures, the effective material parameters can be extracted from the S-parameters as (Chen et al., 2004)

 

 

z and n indicate the refractive index and the wave impedance respectively which are plotted in Figures 8 and 9 respectively. The wave impedance has a positive and refractive index has a negative value at the resonant frequency (Figures 8 and 9). Then, the electrical permittivity and magnetic permeability can be computed from the equations of ε = n/z and µ = n*z. Figures 10 and 11 shows magnetic permeability and electric permittivity respectively which are found to possess negative values at the resonant frequency. Hence conditions for negative refraction have been satisfied for the proposed structure.

 

 

 

This paper successfully demonstrates the metamaterial properties of the unit cell structure by proving the negative refraction within the structure. The approximate numerical results obtained from the equivalent circuit model approach are suggested to describe the resonance behavior of unit cell as well as SRR array. Results obtained from the equivalent circuit model approach are found in very good agreement with the results obtained from HFSS simulations.

Several improvements to enhance the directivity of patch antenna can be taken into consideration for future research. The metamaterial can be designed using different substrate and structures. The metamaterial array of proposed structure can be used as a cover to increase the directive gain and radiation directivity of conventional patch antennas.

The author(s) have not declared any conflict of interest.