Full Length Research Paper
ABSTRACT
Forest operations are associated with products of a biological source and long-term plans. This makes forest management plans affected by market and environmental uncertainties, which can cause differences between the strategic and operational plans. Risks related to disease spread, adverse weather, timber demand, and available capital can cause a reduction in planted areas. It is necessary that forest management plans aim to optimize production and reduce the effects of restrict planting. In this work, a linear programming model was created for long-term forests planning including a variable to restrict planting area. Prescriptions were defined for 6-, 7- and 8-year rotation considering planting or coppicing, creating 60 scenarios varying intensity, period and time of reductions in the planted areas. All scenarios were evaluated by the NPV at the end of the planning horizon. The results showed that the NPV decreased when the planted area was reduced and when the reductions took place at the beginning of the planning horizon. The differences were between 24.1 and 0.07% in relation to the conventional scenario (no planting restriction). The differences were not higher because prescriptions changed from planting to coppice.
Key words: Linear programming, forest planning, planting reduction.
INTRODUCTION
Forest operations deal with products of biological sources on a long-term rotation (Campos and Leite, 2017). The implementation of operational (short-term) management plans is directly affected by many factors, including market demand, economic and silvicultural changes, restrictions of access to stand, different return rates from that planned, an uneven proportion of products, and losses by pests or adverse environmental conditions (Nilsson et al., 2012). Decisions based on these unpredictable factors are often time-sensitive, resulting in noncompliance of what was previously intended in the strategic plan (long-term) (Weintraub and Cholaky, 1991; Davis et al., 2000; Messier et al., 2016; Daniel et al., 2017). Generally, the immediate solutions comprise reprocessing the long-term model (including the operational contingencies) or reprocessing new scenarios. These actions often lead to sub-optimal solutions if compared to the initial long-term proposal, and they do not consider the impact of changes on the long-term feasibility of the forest enterprise (Pukkala, 1998; Thorsen and Helles, 1998; Weintraub and Davis, 1996; Pasalodos-Tato et al., 2013).
Hierarchical planning (long-, medium-, and short-term), is crucial for the survival of any business since it allows optimal allocation of financial, physical, and human resources (Andersson, 2005; Sterk et al., 2009; Bettinger et al., 2017). Therefore, it is imperative to accurately estimate the impacts of changes in forest operations on production and costs compared to the original plan (Machado, 2014), since this influences resource allocation in the future.
In order to assess the impact of changes occurring at tactical and operational levels in the long-term plan, it is valuable to integrate these levels into a single mathematical model (Leuschner et al., 1975; Pasalodos-Tato et al., 2013; Eriksson, 2006; Rodrigues et al., 2006; Nanang and Hauer, 2008). However, depending on model complexity, integration requires the employment of metaheuristics, resulting in sub-optimal solutions (Murray and Church, 1995; Heinonen and Pukkala, 2004; Rodrigues et al., 2004a, b; Zhu et al., 2007; Nascimento et al., 2013; Borges et al., 2014; Bachmatiuk et al., 2015; Bettinger and Boston, 2017). A simpler alternative is to use a mixed-integer programming model (MIP) (Banhara et al., 2010; Öhman and Eriksson, 2010; Tóth et al., 2012), also metaheuristics which allows the quantification of short-term effects of long-term plans. The objective of this study was to analyze and quantify the impact of planting restrictions on management planning and economic indicators at different times of the planning horizon.
MATERIALS AND METHODS
Mathematical model
A mixed-integer programming model was developed using the Regulation Forest Production (RPF) generator (Binoti, 2012). Prescriptions were formulated using planning model type II (Johnson and Scheurman, 1977). Planted areas on plantation prescriptions were modified by varying the planted area (Pk) in the model. This modification allows planting operations assigned on tactical and operational planning levels to differ from the strategic planning previously processed. The constraints for the model were: cut area, minimum and maximum volume, and planting reductions in plantation prescriptions. Since one of the goals was to compare results in scenarios for which planting was not completely done, no forest regulations constrain was implemented.
The planning horizon (PH) was 21 years, and the prescriptions were clear cut with regeneration by planting or coppicing with up to three rotations. Rotations ranged from 6 to 8 years, and the minimum and maximum limits of volumetric demand per period were defined between 65,000 and 90,000 m³. The purchase of timber was considered in periods when production was below the minimum demand.
The mixed-integer programming model developed is as follows:
Objective function:
where R = overall net present value (NPV) (€); n = total number of management units; m = total number of management alternatives for the ith management unit; q = period in the planning horizon; 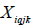 = area (ha) of management unit i, in number of the periods q coming from the jth prescription in period k;
= area (ha) of management unit i, in number of the periods q coming from the jth prescription in period k; 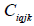 = net present value (NPV) per area (ha) of the ith management unit cut in period q, implementing the jth prescription;
= net present value (NPV) per area (ha) of the ith management unit cut in period q, implementing the jth prescription;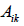 = area of management unit i in year k;
= area of management unit i in year k;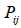 = prescription j for management unit i;
= prescription j for management unit i;  = respectively, minimum and maximum volumetric demands (m³) in each period k of the planning horizon;
= respectively, minimum and maximum volumetric demands (m³) in each period k of the planning horizon; 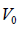 = volume per hectare (m³ha-1) at age 0, defined by the production table;
= volume per hectare (m³ha-1) at age 0, defined by the production table; 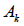 = areas with prescriptions j in period k;
= areas with prescriptions j in period k; 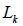 = areas effectively planted on prescription j after cut in period k;
= areas effectively planted on prescription j after cut in period k;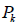 = rate of planted area in period k with prescription j.
= rate of planted area in period k with prescription j.
Scenario simulation
Data from a model property located in Minas Gerais State, Brazil, with 18 management units (MU) and 1800 ha were used. At the beginning of PH, the area was divided into eight age groups (1, 2, 3, 4, 5, 6, 7 and 8 years), with 225 ha each. The productivity (Table 1) was provided by the forestry company where the stands are located. Silviculture and harvesting costs were adapted from a formula developed by Binoti (2010) (Table 1). Harvesting costs were divided into two strata according to the difficulty of harvesting in each plot (Table 2). The amounts were converted from the Brazilian currency to euros (€) using the conversion factor 3.89 (€ 1.00 = R$ 3.89) for 20 December 2017 (European Central Bank, 2019).
The interest rate used was 8% per year, timber price was set at 12.85 (€/m³), and the residual value of timber after the planning horizon was 12.85 (€/m³). The model was processed using Lingo (15.0), granted to this study by Lindo Systems Inc. (http://www.lindo.com).
Sixty scenarios were simulated with the variation in the restriction in the planted area (Pk) modifying the plantation prescriptions. In these scenarios, the areas scheduled for planting in the strategic plan differed from the areas where planting was done. This change was based on aspects such as area loss, cost reductions, and planting problems. The net present value (NPV) obtained by the new scenarios was compared and analyzed by gains or losses due to the changes. Furthermore, groups of scenarios were created varying the rate of planted area reduction (e.g., 0% or not planting, 10%, 20%, …, 100% of the area), and the period within the planning horizon of these reductions occurred. Therefore, the options for the reductions in the planted areas were:
(1) Planting entire area, schedule for this purpose, in all years;
(2) Planting 90, 80, ..., 0% of the area in the initial third of the Planning Horizon (PH) (1st to 7th year);
(3) Planting 90, 80, ..., 0% of the area in the middle third of the PH (8th to 14th year);
(4) Planting 90, 80, ..., 0% of the area in the final third of the PH (15th to 21st year);
(5) Planting 90, 80, ..., 0% of the area in the initial half of the PH (1st to 11th year);
(6) Planting 90, 80, ..., 0% of the area in the final half of the PH (12th to 21st year);
(7) Planting 90, 80, ..., 0% of the area in all years.
RESULTS AND DISCUSSION
All solutions were economically feasible except when the areas were not planted in any period of the PH (100% planting restricted). In this scenario, it was not possible to meet the minimum demand in any period due to the exhaustion of timber stock. Whereas, in the other scenarios, the reduction in planted areas resulted in a modest overall NPV reduction and required timber purchase in some periods of the PH.
In the conventional scenario in which the entire area was planted, timber purchase was not necessary, the NPV was € 6,884,982.01, and timber volume did not significantly variate over the years, even though there were no restrictions accounting for regulation in the model (Figure 1).
The NPV decreased following the restrictions in the planted area (Figure 2). This reduction was driven by the selection of coppicing over planting the stands, considering that sprouts usually yield less.
Planting restrictions at the beginning of the PH result in lower NPV at the end. This is because timber volume production is already compromised at the beginning of the PH due to the selection of coppice prescriptions, yielding less timber volume when compared with plantations. In some groups of scenarios, the NPV is slightly variated. This demonstrates that, even with lower yields in coppice prescriptions, it is an option for periods when there is no availability for planting in harvested areas.
When the restrictions in the planted area variated during the initial third of the PH (1st to 7th year), the NPV gradually decreased. When there was no planting (0% of the area planted), the loss in NPV was 8.06%, whereas when 90% of the area was planted, the difference was €6,246.79, representing a loss of 0.09% (Table 3) if compared to the expected scenario (planting the entire area). In addition, it was necessary to purchase timber in some of the scenarios (for example the scenario with 0% of planting, which had timber purchased in period 11, and the scenario with 30% of planting, where timber was purchased in periods 11 and 18).
Similarly, during the middle third of the PH (8 to 14th year), this group also experienced a gradual reduction in the NPV. Specifically, for the scenario in which there was no planting, the difference from the conventional was €55,781.49, (0.81% loss on investment), while for the minimum reduction (90% of planting area), the difference was €40,843.18 (0.593% loss) (Table 3). These groups did not require timber purchase since all demands were satisfied (Figure 2b).
In the final third of the PH (15th to 21st year), the NPV reduced €38,035.99 (0.552% difference from the conventional scenario) when the planting area reduced from 80 to 0% of the area. The minimum reduction (90% of planting) led to an NPV increase of €622.11 (Table 3).
Scenarios with restrictions in the planted area in the middle third and in the final third of the PH had lower NPV decreases compared to scenarios of the initial third (Table 4). In this group, planting prescriptions occurred at least once, so the timber demand for all periods was satisfied. Similar to that group with planting reductions in the middle third of the PH, timber purchase was not necessary for any period for planting reductions in the final third of the PH (Figure 2c).
The scenarios of planting restrictions in the initial half of the PH (1st to 11th year) showed a reduction of 10.14% in the NPV, representing a loss of €697,565.55, with 0% of planting. On reductions from 70 to 0% of the planted area, it was necessary to purchase timber in at least one period, resulting in the highest purchased volumes in 0 and 10% of planting, with 65,000 and 56,634 m³, respectively (Figure 2d).
Planting restrictions in the final half of the PH (12th to 21st year) did not result in large NPV variations, similar to in the middle and final thirds of the PH. The greatest NPV difference in this group was 1.61%, which represents a loss of €115,203.09 (Table 3). The reason timber demand was satisfied in this case was the selection of planting prescriptions at the beginning of the PH. Hence, all timber demands were met for this group, and no timber purchase was required in any period (Figure 2e and f).
The scenario with planting restrictions in all periods of the PH resulted in the lowest NPV, indicating that not restoring forest resources can lead to exhaustion of forest timber stock. Although scenarios with planting reduction at the end of the PH resulted in higher NPV, the influence of timber shortage will arise in the next PH. This effect will be either due to the reduction of the planted area or by choosing coppice prescriptions.
Scenarios resulting in the highest NPV losses were those with planting reduction (90 to 0% of the area planted) in all years of the PH. The losses were from 24.1% when planting 10% in all years and from 2.33% when planting 90% in all years. In scenarios with 0 to 70% of planting, it was necessary to purchase timber in at least one period (Figure 2).
Application of operational research tools in hierarchical forest planning can contribute meaningfully to decision-making (Fonseca et al., 2012; Martins et al., 2014; Hahn et al., 2014; Garcia-Gonzalo et al., 2016; Carvalho et al., 2016). However, because of the relatively large PH, there are several risks and uncertainties that this model is unable to predict (e.g. economic fluctuations, area loss by wildfire or disease, and budget cutbacks) (Kangas and Kangas, 2004; Eyvindson and Kangas, 2018). In these cases, there is an impact on the optimization response of the model at the strategic, tactical, and operational levels.
The restrictions in planted areas decreased the NPV in all scenarios in relation to the three dimensions of the decision variable: intensity (90 to 0% of the area), time, and period. Changes in all dimensions showed a tendency to exhaust forest resources that are withdrawn and not restored. Regarding intensity, it was verified in all scenarios that, the greater the reduction in the planted area, the lower the NPV. This indicates that, although planning can absorb part of the reductions by selecting coppice prescriptions, the yield will be lower compared to those when the areas were completely planted. Temporally, NPV losses were greater when they occurred earlier in the PH because of the reduction of areas available for production and future harvest. However, losses with reductions at the end of the PH will be incurred after the transition period due to the timber shortage failing to supply the minimum demand during the next first periods. The period when restrictions occurred also had a direct relationship to NPV decrease. Incomplete planting in one third, half, or in all periods of the PH was directly related to the reduction of NPV when compared with the scenario where there was no change in planting.
CONCLUSION
The model proposed in this study is effective in verifying the impact of restrictions in the planted area on forest planning and can be used as decision criteria as it shows the effects of not investing in planting after harvesting the stand. Although the model was tested only with reductions in planted areas, it can be used in situations where there are uncertainties such as an increase/decrease in planted areas or in timber volume demand.
Suggestions for future studies include: (1) simulate planting restrictions scenarios in interleaved years and verify whether the final revenue variation is lower; (2) simulate scenarios of increase or decrease in planting areas and verify whether planting new areas can absorb the revenue loss emerged from the restrictions; and (3) simulate variations in interest rate, stumpage, forest yield, and timber purchase price, modifying the objective function to maximize production and reduce cost.
CONFLICT OF INTERESTS
The authors have not declared any conflict of interests.
REFERENCES
|
Andersson D (2005). Approaches to Integrated Strategic/Tatical Forest Planning. Swedish University of Agricultural Sciences, Department of Forest Resource Management and Geomatics, Umeå, Sweden. |
|
|
Bachmatiuk J, Garcia-Gonzalo J, Borges JG (2015). Analysis of the performance of different implementations of a heuristic method to optimize forest harvest scheduling. Silva Fennica 49(4):1-18. |
|
|
Banhara JR, Rodriguez LCE, Seixas F, Moreira JMMÁP, Silva LMS, Nobre SR, Cogswell A (2010). Agendamento otimizado da colheita de madeira de eucaliptos sob restrições operacionais, espaciais e climáticas]. Scientia Forestalis 38(85):85-95. |
|
|
Bettinger P, Boston K, Siry J, Grebner D (2017). Forest management and planning 2nd ed. Academic Press: London, UK. |
|
|
Bettinger P, Boston K (2017). Forest Planning Heuristics - Current Recommendations and Research Opportunities for s-Metaheuristics. Forests 8(12):476. |
|
|
Binoti DHB (2012). Sistemas computacionais aplicados ao manejo florestal . Universidade Federal de Viçosa, Viçosa, MG, Brazil. 113p. |
|
|
Binoti DHB (2010). Estratégias de regulação de florestas equiâneas com vistas ao manejo da paisagem . Universidade Federal de Viçosa, Viçosa, MG, Brazil. 145p. |
|
|
Borges P, Eid T, Bergseng E (2014). Applying simulated annealing using different methods for the neighborhood search in forest planning problems. European Journal of Operational Research 233(3):700-710. |
|
|
Campos JCC, Leite HG (2017). Mensuração Florestal: Perguntas e Respostas, 5th ed. Editora UFV, Viçosa, MG, Brazil. |
|
|
Carvalho KHA, Silva ML, Leite HG, Binoti DHB, Silva LF (2016). Influência de diferentes funções objetivo em modelos de regulação florestal. Revista Agroambiente 10(4):371-380. |
|
|
Daniel CJ, Ter-mikaelian MT, Wotton BM, Rayfield B, Fortin MJ (2017). Incorporating uncertainty into forest management planning : Timber harvest, wildfire and climate change in the boreal forest. Forest Ecology and Management 400(15):542-554. |
|
|
Davis L, Johnson KN, Bettinger P, Howard T (2000). Forest Management, 4th ed. McGraw-Hill, New York, N.Y., USA. |
|
|
European Central Bank (2019). |
|
|
Eriksson LO (2006). Planning under uncertainty at the forest level: A systems approach. Scandinavian Journal of Forest Research 21(56):111-117. |
|
|
Eyvindson K, Kangas A (2018). Guidelines for risk management in forest planning - what is risk and when is risk management useful? Canadian Journal of Forest Research 48(4):309-316. |
|
|
Fonseca TF, Cerveira A, MotaA(2012). An integer programming model for a forest harvest problem in Pinus pinaster stands. Forest Systems 21(2):272-283. |
|
|
Garcia-Gonzalo J, Pais C, Bachmatiuk J, Weintraub A (2016). Accounting for climate change in a forest planning stochastic optimization model. Canadian Journal of Forest Research 46(9):1111-1121. |
|
|
Hahn WA, Härtl F, Irland LC, Kohler C, Moshammer R, Knoke T (2014). Financially optimized management planning under risk aversion results in even-flow sustained timber yield. Forest Policy and Economics 42:30-41. |
|
|
Heinonen T, Pukkala T (2004). A comparison of one- and two-compartment neighbourhoods in heuristic search with spatial forest management goals. Silva Fennica 38(3):319-332. |
|
|
Johnson KN, Scheurman HL (1977). Techniques for Prescribing Optimal Timber Harvest and Investment Under Different Objectives-Discussion and Synthesis. Forest Science 23(1):1-31. |
|
|
Kangas AS, Kangas J (2004). Probability, possibility and evidence: approaches to consider risk and uncertainty in forestry decision analysis. Forest Policy and Economics 6(2):169-188. |
|
|
Leuschner WA, Porter JR, Reynolds MR, Burkhart HE (1975). A Linear Programming Model for Multiple-use Planning. Canadian Journal of Forest Research 5(3):485-491. |
|
|
Machado CC (2014). Planejamento e colheita florestal, 3rd ed. Editora UFV, Viçosa, MG, Brazil. |
|
|
Martins I, Ye M, Constantino M, Fonseca MC, Cadima J (2014). Modeling target volume flows in forest harvest scheduling subject to maximum area restrictions. Top 22(1):343-362. |
|
|
Messier C, Puettmann K, Filotas E, Coates D (2016). Dealing with Non-linearity and Uncertainty in Forest Management. Current Forestry Reports 2(2):150-161. |
|
|
Murray AT, Church RL (1995). Heuristic solution approaches to operational forest planning problems. Operations-Research-Spektrum 17(2):193-203. |
|
|
Nanang DM, Hauer GK (2008). Integrating a random utility model for non-timber forest users into a strategic forest planning model. Journal of Forest Economics 14(2):133-153. |
|
|
Nascimento FAF, Arce JE, Dias AN, Figueiredo-Filho A, Miranda GM, Carnieri C (2013). Meta-Heurística Otimização por Enxame de Partículas Aplicada ao Planejamento Florestal. In: Lopes HS, Rodrigues LCA, Steiner MTA (eds.) Meta-Heurísticas em Pesquisa Operacional Omnipax, Curitiba, PR, Brazil. pp. 355-366. |
|
|
Nilsson M, Westerlund DS, Wahlberg O, Eriksson LO (2012). Forest planning in a Swedish company - a knowledge management analysis of forest information. Silva Fennica 46(5):717-731. |
|
|
Öhman K, Eriksson L (2010). Aggregating harvest activities in long term forest planning by minimizing harvest area perimeters. Silva Fennica 44(1):77-89. |
|
|
Pasalodos-Tato M, Mäkinen A, Garcia-Gonzalo J, Borges JG, Lämås T, Eriksson LO (2013). Assessing uncertainty and risk in forest planning and decision support systems : review of classical methods and introduction of innovative approaches. Forest Systems 22(2):282-303. |
|
|
Pukkala T (1998). Multiple risks in multi-objective forest planning: Integration and importance. Forest Ecology and Management 111(2-3):265-284. |
|
|
Rodrigues FL, Leite HG, Santos HN, Souza ALS, Ribeiro CAAS (2004a). Metaheurística Simulated Annealing para solução de problemas de planejamento florestal com restrições de integridade. Revista Árvore 28(2):247-256. |
|
|
Rodrigues FL, Leite HG, Santos HN, Souza AL, Silva GF (2004b). Metaheurística algoritmo genético para solução de problemas de planejamento florestal com restrições de integridade. Revista Árvore 28(2):233-245. |
|
|
Rodrigues FL, Silva GF, Leite HG, Xavier AC, Pezzopane JEM (2006). Um modelo de regulação florestal e suas implicações na formulação e solução de problemas com restrições de recobrimento. Revista Árvore 30(5):769-778. |
|
|
Sterk B, Leeuwis C, Van Ittersum MK (2009). Land use models in complex societal problem solving: Plug and play or networking? Environmental Modelling and Software 24(2):165-172. |
|
|
Thorsen BJ, Helles F (1998). Optimal stand management with endogenous risk of sudden destruction. Forest Ecology and Management 108(3):287-299. |
|
|
Tóth SF, Mcdill ME, Könny N, George S (2012). A Strengthening Procedure for the Path Formulation of the Area-Based Adjacency Problem in Harvest Scheduling Models. Mathematical and Computacional Forestry and Natural-Resource Sciences 4(1):27-49 |
|
|
Weintraub A, Cholaky A (1991). A Hierarchical Approach to Forest Planning. Forest Science 37(2):439-460. |
|
|
Weintraub A, Davis L (1996). Hierarchical planning in forest resource management: defining the dimensions of the subject area. In: Proceedings of a workshop on hierarchical approaches to forest management in public and private organizations. Martell DL, Davis LS, Weintraub A (eds). Petwawa National Forestry Institute. Information Report PI-X-124. pp. 2-14. |
|
|
Zhu J, Bettinger P, Li R (2007). Additional insight into the performance of a new heuristic for solving spatially constrained forest planning problems. Silva Fennica 41(4):667-698. |
|
Copyright © 2024 Author(s) retain the copyright of this article.
This article is published under the terms of the Creative Commons Attribution License 4.0