International Journal of
Science and Technology Education Research

  • Abbreviation: Int. J. Sci. Technol. Educ. Res.
  • Language: English
  • ISSN: 2141-6559
  • DOI: 10.5897/IJSTER
  • Start Year: 2010
  • Published Articles: 79

Full Length Research Paper

Single basis function method for solving diffusion convection equations

Sunday Babuba
  • Sunday Babuba
  • Department of Mathematics, Federal University Dutse, Ibrahim Aliyu Bye-Pass, P. M. B. 7156, Dutse, Jigawa State, Nigeria.
  • Search for this author on:
  • Google Scholar


  •  Received: 26 June 2017
  •  Accepted: 24 August 2017
  •  Published: 30 September 2017

 ABSTRACT

In this study, we developed a new numerical finite difference method for solving various diffusion convection equations. The method involves reduction of the diffusion convection equations to a system of algebraic equations. By solving the system of algebraic equations we obtain the problem approximate solutions. The study of the numerical accuracy of the method has shown that the method provides similar results to the known explicit finite difference method for solving diffusion convection equations, but with fewer numbers of iterations.

Key words: Lines, multistep collocation, parabolic, Taylor’s polynomial.


 INTRODUCTION

In this study, we will deal with diffusion convection equations, where and are the time and space coordinates respectively, and the quantities and are the mesh sizes in the space and time directions.
 
We consider,
 
 
A special type of diffusion convection equation where   are constants, defined for and positive time with appropriate initial and boundary conditions, and    is  the  temperature  in  the  medium. We are interested in the development of numerical techniques for solving diffusion convection equations. Recently, there is a growing interest concerning continuous numerical methods of solution for Ordinary Differentials Equations (ODEs) (Adam and David, 2002; Awoyemi, 2002, 2003; Bao et al., 2003; Benner and Mena, 2004; Bensoussan et al., 2007; Motmans et al., 2005; Brown, 1979; Chawla and Katti, 1979; Cook, 1974; Crandall, 1955; Crane and Klopfenstein, 1965; Crank and Nicolson, 1947; Dahlquist and Bjorck, 1974; Dehghan, 2003; Dieci, 1992; Douglas, 1961; D’ Yakonov and Ye, 1963; Eyaya, 2010; Fox, 1962; Penzl, 2000; Pierre, 2008; Richard and Albert, 1981; Richard et al., 2001; Saumaya et al., 2012; Yildiz and Subasi, 2001; Zheyin and Qiang, 2012). We are interested in the  extension  of a  particular continuous method to solve the diffusion convection equation. This is done based on the collocation and interpolation of the Partial Differential Equations (PDEs) directly over multi steps along lines but with reduction to a system of ODEs.


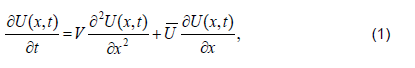
 THE SOLUTION METHOD

 
Writing Equation 4 as matrix in its augmented form, we have
 
 
 
Writing Equation 16 as matrix in augmented form, we have
 


 ADVANTAGE OF THE NEW SCHEME OVER FINITE DIFFERENCE METHOD

The new scheme requires fewer numbers of iterations than the finite difference method to achieve the same results.


 NUMERICAL EXAMPLES

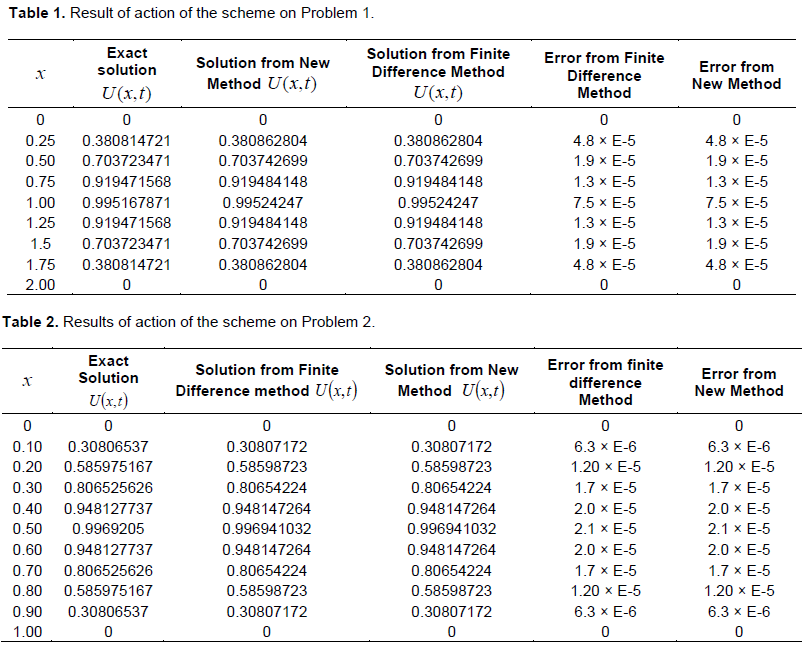
Here, we will test the numerical accuracy of the new method by using the scheme to solve two test examples. We compute an approximate solution of Problems (1) and (2) at each time level (Tables 1 and 2). To achieve this, we truncate the polynomials after second degree.
 


 SPECIFIC PROBLEM

Example 1
 
Here we use  the  scheme to  approximate the solution to the diffusion convection equation (Table 1)
 
 
Example 2
 
Here we use the scheme to approximate the solution to the diffusion convection equation (Table 2)
 


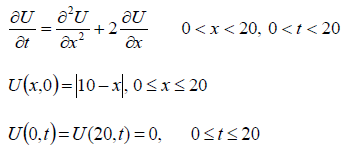
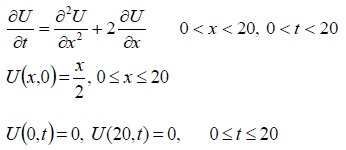
 CONCLUSION

A numerical method which involves the discretization of the diffusion convection equations to a system of algebraic equations is formulated for solving diffusion convection problems. To check the accuracy of the numerical method, it is applied to solve two different test problems with known finite difference solutions. The overall numerical results obtained showed that the values obtained are the same with the results of the finite difference method. These confirmed the validity of the new numerical scheme and suggested that it is an interesting and viable numerical method.


 CONFLICT OF INTERESTS

The author has not declared any conflict of interests.



 REFERENCES

Adam A, David R (2002). One dimensional heat equation. 
 

Awoyemi DO (2002). An Algorithmic collocation approach for direct solution of special fourth–order initial value problems of ordinary differential equations. J. Nigerian Association of Math. Phys. 6:271-284.

  
 

Awoyemi DO (2003). A p-stable linear multistep method for solving general third order Ordinary differential equations. Int. J. Comput. Math. 80(8):987-993.
Crossref

  
 

Bao W, Jaksch P, Markowich PA (2003). Numerical solution of the Gross – Pitaevskii equation for Bose – Einstein condensation. J. Compt. Phys. 187(1):318-342.
Crossref

  
 

Benner P, Mena H (2004): BDF methods for large scale differential Riccati equations. Proc. of Mathematical theory of network and systems. MTNS. Edited by Moore, B. D., Motmans, B., Willems, J., Dooren, P.V. & Blondel, V.

  
 

Bensoussan A, Da Prato G, Delfour M, Mitter S (2007). Representation and control of infinite dimensional systems. 2nd edition. Birkhauser: Boston, MA.
Crossref

  
 

Motmans B, Willems J, Dooren PV, Blondel V, Biazar J, Ebrahimi H (2005). An approximation to the solution of hyperbolic equation by a domain decomposition method and comparison with characteristics method. Appl. Math. Comput.163:633-648.
Crossref

  
 

Brown PLT (1979). A transient heat conduction problem. AICHE J. 16:207-215.

  
 

Chawla MM, Katti CP (1979). Finite difference methods for two-point boundary value problems involving high-order differential equations. BIT. 19:27-39.
Crossref

  
 

Cook RD (1974). Concepts and Application of Finite Element Analysis: NY: Wiley Eastern Limited.

  
 

Crandall SH (1955). An optimum implicit recurrence formula for the heat conduction equation. Q. Appl. Math. 13(3):318-320.
Crossref

  
 

Crane RL, Klopfenstein RW (1965). A predictor – corrector algorithm with increased range of absolute stability. JACM 12:227-237.
Crossref

  
 

Crank J, Nicolson P (1947). A practical method for numerical evaluation of solutions of partial differential equations of heat conduction type. Proc. Camb. Phil. Soc. 6:32-50.
Crossref

  
 

Dahlquist G, Bjorck A (1974). Numerical methods. NY: Prentice Hall.

  
 

Dehghan M (2003). Numerical solution of a parabolic equation with non-local boundary specification. Appl. Math. Comput. 145, 185-194.
Crossref

  
 

Dieci L (1992). Numerical analysis. SIAM J. 29(3):781-815.

  
 

Douglas J (1961). A survey of numerical methods for parabolic differential equations in advances in computer II. Academic Press. D' Yakonov, Ye G (1963). On the application of disintegrating difference operators. USSR Computational Mathematics and Mathematical Physics, 3(2):511-515.

  
 

Eyaya BE (2010). Computation of the matrix exponential with application to linear parabolic PDEs.

  
 

Fox L (1962). Numerical Solution of Ordinary and Partial Differential Equation. New York: Pergamon.

  
 

Penzl T (2000). A cyclic low-rank Smith method for large sparse Lyapunov equations. SIAM J. Sci. Comput. 21(4):1401-1418
Crossref

  
 

Pierre J (2008). Numerical solution of the dirichlet problem for elliptic parabolic equations. SIAM J. Soc. Ind. Appl. Math. 6(3):458-466.

  
 

Richard LB, Albert C (1981). Numerical analysis. Berlin: Prindle, Weber and Schmidt, Inc.

  
 

Richard L, Burden J, Douglas F (2001). Numerical analysis. Seventh ed., Berlin: Thomson Learning Academic Resource Center.

  
 

Saumaya B, Neela N, Amiya YY (2012). Semi discrete Galerkin method for equations of Motion arising in Kelvin – Voitght model of viscoelastic fluid flow. J. Pure Appl. Sci. 3(2 & 3):321-343.

  
 

Yildiz B, Subasi M (2001). On the optimal control problem for linear Schrodinger equation. Appl. Math. Comput.121:373-381.
Crossref

  
 

Zheyin HR, Qiang X (2012). An approximation of incompressible miscible displacement in porous media by mixed finite elements and symmetric finite volume element method of characteristics. Appl. Math. Computat. Elsevier 143:654-672.

  

 




Copyright © 2024 Author(s) retain the copyright of this article.

This article is published under the terms of the Creative Commons Attribution License 4.0

Back to Vol. 8 No. 2
Back to articles
SUBSCRIBE TO RSS
SUBMIT MANUSCRIPT
CONFERENCES
          */?>