ABSTRACT
The purposes of this study were to explore the nature of the teaching-learning process in line with active learning methods and to identify the major challenges hindering the implementation of these approaches in mathematics classes. Both qualitative and quantitative methods of data collection were employed which is a mixed method research design. Probability proportional sampling technique for students and availability sampling technique for teachers were used. 25 mathematics teachers and 369 students were involved in the study. Questionnaires, lesson observation, and focus groups discussion were the data gathering instruments. The quantitative data obtained were analyzed using SPSS. The qualitative data were analyzed by narrating the information obtained from the data. Questioning method, group work, gap lecture, cooperative learning, and individual work were the methods used commonly by the teachers. Large class size; the amount of content to be covered; lack of instructional materials; lack of administrative support; and that it took too much effort from teachers are main challenges that hinder the application of active learning methods in the classrooms.
Key words: Active learning, challenges of active learning, constructivism, student centered.
Teaching for understanding is an agenda in educational practice that has been receiving significant interest in international educational communities since the late 1980s (Rutherford and Ahlgren, 1990; Wiske, 1998). In other contexts, it is called ‘active learning’ (Organization for Economic Co-operation and Development, 1993), ‘higher-level cognitive learning’ and ‘teaching for the twenty-first century’ (NCTM, 2000). Teaching for understanding (active learning) helps learners to develop their potential as individuals and to make responsible decisions for living and working in the 21st century.
Mathematics helps us think analytically and have better reasoning abilities. Analytical thinking refers to the ability to think critically about the world around us. Analytical and reasoning skills are important because they help us solve problems and look for solutions. Mathematics learning should be about developing conceptual understanding in order to prepare our students for the 21st Century. Successful 21st Century mathematics learning needs to foster 21st Century skills such as communication, collaboration, critical thinking and problem solving.
The overall quality of teaching and learning is improved when students have full opportunities to clarify, question, apply and consolidate new knowledge. In this case, teachers create opportunities for students to engage new material, serving as guides to help them understand and apply information. Student achievement in mathematics increases through mastery of content as a result of active learning techniques. Active learning, at the same time, is a social process that also has recorded multiple benefits for the academic achievements of students on various levels. In the process of solving mathematical problems, such learning can be utilized to attain optimal outcome and build a foundation for the future of students’ learning. Students also develop improved problem solving, communication, and higher order thinking skills.
Research has consistently shown that students’ attention and concentration during straight lectures tend to drop off dramatically after 15 to 20 minutes (Penner, 1984; Verner and Dickinson, 1967) even among highly motivated postgraduate students (Stuart and Rutherford, 1978). This is because learning is by its nature an active process that requires engagement and the use of higher order thinking skills such as analyzing, synthesizing and evaluating scientific or mathematical problems and findings.
The teacher-centered method of teaching has a little effect on mathematics learning of students in which the majority of teachers reported that they were not succeeding in teaching concepts of mathematics (Melaku and Solomon, 2013). Thus, regarding teaching methods, researchers reached on the conclusion that if we want students to become more effective in meaningful learning and thinking, they need to spend more time in active, meaningful learning and thinking, not just sitting and passively receiving information (McKeachie et al., 1986).
Based on this aim in mind, the following basic questions guided this study.
1. Do mathematics teachers use active learning methods in their classroom instructions in schools?
2. What types of active learning methods do teachers use in mathematics classroom instructions?
3. What are the challenges affecting the implementation of active learning methods in schools?
REVIEW OF RELATED LITERATURES
Definitions of active learning
All learning is active in a certain sense, but some kinds of learning are more active than others. A formal definition by Meyers and Jones states that active learning is learning that allows “students to talk and listen, read, write, and reflect as they approach the course content through problem-solving exercises, small informal groups, simulations, case studies, role-playing, and other activities all of which require students to apply what they are learning” (Meyers and Jones, 1993). Active learning can also be generally defined as any instructional method that engages students in the learning process (Prince, 2004). In short, active learning requires students to do meaningful learning activities and think about what they are doing. The core elements of active learning are student activity and engagement in the learning process.
Active learning methods are widely spread in today’s classrooms and are often associated with constructivism. Although constructivism was not a pedagogical paradigm, many of its followers developed practical applications of the theory in learning practice. Constructivist learning theory emphasizes that individuals learn through building their own knowledge, connecting new ideas and experiences to existing knowledge and experiences to form new or enhanced understanding (Bransford et al., 1999).
Effective strategies for teaching elementary mathematics
Teaching in today's mixed-ability classroom can be a challenge. These days, it is not uncommon to find a wide range of abilities in one classroom: From students struggling to grasp new concepts, to those who are way ahead of their peers from day one. This factor has contributed to a range of problems for early mathematics learners, including a large achievement gap between students. While individual students do benefit from different learning styles, there are ranges of effective strategies that can help all students to succeed. Some effective strategies for teaching elementary mathematics are making it hands-on; using visuals and images; showing and telling new concepts and giving feedback.
Instructional strategies that facilitate active learning
Active learning instructional strategies include a wide range of activities that share the common element of involving students in doing things and thinking about the things they are doing (Bonwell and Eison, 1991). Active learning instructional strategies can be created and used to engage students in thinking critically or creatively, speaking with a partner, in a small group, or with the entire class, expressing ideas through writing, exploring personal attitudes and values, giving and receiving feedback, and reflecting upon the learning process. It should also be noted that active learning instructional strategies can be completed by students either in-class or out-of-class, be done by students individually or in groups. Some instructional strategies that facilitate active learning are using effective questioning strategies to elicit student involvement in class; acknowledging the name of the student who gave a response voluntarily; recording student ideas on the blackboard; occasionally redirecting questions directed at teachers to other students in class by asking volunteers to answer the question etc.
Teachers' interest in active learning
Teachers are interested in active learning for several reasons. They are aware that students must be prepared for continual learning throughout their lifetimes. Teachers experience the need for continual learning in their own professional lives, due in part to professional development programs that are provided for them. Teachers are also aware of accumulating research on how people learn. As the constructivist paradigm has come to dominate educational research, educational literature, and teaching in schools of education, it has exerted a strong force on practicing teachers.
Obstacles to active learning in classrooms
Despite teachers' interest in active learning, they are not always able to arrange for students to do it. One obstacle is that some students find it threatening. They do not want the challenge, or they are more comfortable in a more passive role. Another barrier is the possible conflict with required curriculum and accompanying examinations. Active learning projects take time. They may deepen students' understanding of certain ideas, but teachers may be concerned about sacrificing breadth of coverage. If students' opportunities for further education depend on broad knowledge of material in the required syllabus, there may be little time for active learning. There is a basic contradiction between the goal of developing students' capacity to manage their own learning including the capacity to make good decisions about what to learn and the goal of teaching a predetermined school curriculum.
On the other hand, some forms of active learning within the classroom can actually reduce some of the routine tasks teachers have to do, though this may not be evident at first. In co-operative learning, students are sometimes given responsibility for checking and correcting one another's works. This gives the teacher more time to work with students individually.
This leads to another obstacle, which is the necessity for teacher training. It is not sufficient for teachers merely to be told about a different way to teach. They need the opportunity for active learning. This begins by experiencing the new approach from the position of a student, and progresses to trying out the role of a teacher organizing learning processes for others. After supervised practice with the new method, teachers can be ready to use it in their own classrooms, but even then their effectiveness in implementing the new technique was greater if they continue to receive assistance.
Several impediments to active learning have to do with student characteristics. The first student factor concerns learning conceptions. Students differ in the way they see the fundamentals of learning and the division of tasks between teachers and students. On the one hand, there were students who regard learning as copying ideas and information out of books and the heads of teachers into their own heads. These students tend to see teachers as responsible for structuring presentations and assignments.
A second set of impediments to active learning has to do with learning goals. Many students do not think about the goals of learning, they take learning for granted (Saljo, 1979; Thomas and Harri-Augstein, 1985). A related problem concerns students' perceptions of tests and exam demands. Even if teachers value higher-level students as stressing, lower level students often perceive goals in their testing practices. Motivational, volitional (deliberate intention) and affective factors may impede active learning. For instance, there are students who are afraid of changing their learning approach. Some students, trying to reduce uncertainty, practice active learning in an unproductive way.
Furthermore, students may fail to believe that active learning really "works" (that is, that you can remember information just by thinking about it). Some students also believe that active learning requires too much effort or energy. Students who do not believe that they are able to learn in active way and reach acceptable or even better results (lack of self-confidence), may not even try to engage in it. A fourth impediment concerns the skill of active learning itself. Students who do not use certain activities will lack the necessary learning skills (elaboration, analyzing, etc.). Many students also lack regulation skills.
Borkowski and Muthukrishna (1992) described metacognitive models of learning of teachers that form obstacles to active learning. Many teachers believe that learning occurs when students reach a certain task goal by doing what the teacher says. Teachers may hesitate to hand over responsibility to their students because the students are not prepared for it but this keeps the students perpetually unprepared. Larsson (1983) found that some teachers would like to give students more freedom to learn, but do not believe that students are able to handle this freedom.
Other obstacles are lack of teaching materials for active learning, and the pressure of exams. Publishers and textbooks are, generally not suited for active learning. Finally, examination requirements may inhibit active learning. Teachers often believe, rightly or not, that material that will appear on exams must be taught through lectures. This is connected with the fact that many teachers consider themselves in the first place expert in a certain field and only in the second place a professional communicator and educator.
The classroom conditions
The condition of the classroom is one of the most important factors that should be considered in the teaching-learning process in general and active learning in mathematics education in particular. Burns and Myhill (2004) point out that the physical environment in classrooms can make or break active learning approaches. Thus, to engage students in learning activities the classroom should be well equipped with furniture. There should be a movable desk for every student to use different layouts in the classroom. In another study, Silberman in Zweck (2006) suggested 10 different types of classroom layouts, which facilitate active learning approaches. These layouts include a U-shape, team style, conference table, circle, group on group, workstation breakout grouping, traditional classroom, auditorium arrangements etc.
Class size
Class size refers to the number of students that regularly attend a class section at a certain grade level. It has its own impact on the teaching-learning process in general and on the implementation of active learning in particular. As the class size increases, students face any or all of the following problems: Lack of clarity of purpose; knowledge about progress; advice on improvement; lack of opportunity to discussion; inability to support independent study and inability to motivate students. In contrast to the above, Jarvis (Slavin, 2005) suggests that class size is not a significant factor in students’ achievement. He found that individual teachers varied in their effectiveness in different class sizes. Some were more effective in large classes than in small ones, while others were less effective in large classes than in small ones. Other researchers have taken middle position. As stated by McKeachie (1999) whether a large or a small group is appropriate depends on the following factors: Learning objective that are to be realized; nature of the subject to be taught; pupil attention and learning resources.
Research design
The study was conducted at six governmental second cycle primary schools (Grades 5 to 8) in Woliso town of Oromia regional state, Ethiopia. These schools were selected by available sampling technique since there are only six government primary schools in the town. The design of the research was descriptive survey type.
The method involved the survey that describes the status quo and a brief discussion with an individual about a specific topic. Both qualitative and quantitative methods of data collection were employed which is a mixed method research design.
Subjects of the study
The subjects of the study were students (grades 5- 8) and mathematics teachers of the schools in the academic year of 2019. All mathematics teachers in the selected schools were taken as sources of data. On this regard, 25 mathematics teachers participated in the study from the selected schools. By using probability proportional to size (pps) sampling method, from the total populations of 4882 grades 5 to grade 8 students, the sample of 369 students were selected from the sample schools.
Data collection instruments
In this study, questionnaire, classroom observation and focus group discussion were used as instruments of data collection. Teacher’s questionnaire was administered to 25 mathematics teachers teaching in the selected schools and only 21 of them were returned it. Teachers responded to a four point Likert Scale on different items concerning their use of active teaching/learning approaches and the major problems/challenges that hinder them for the implementation of active learning approach in schools. Students’ questionnaire was administered to 369 students of which 360 of them were returned and analyzed to study the use of active learning techniques and to identify challenges that hinder to use the techniques in their classrooms. The researcher explained the purpose of the questionnaire and gave detail instruction on how to fill all the items face to face with all the students in the selected schools.
In addition to this, the researcher sat in the participants’ class during their regular mathematics period, observed the teaching learning process, and recorded it by using an observation checklist prepared earlier. In addition to this, the researcher recorded what he saw, heard, and experienced activities during a teaching session that are not included in the checklist (Gay and Airasian 2000). In total 6 lessons (one period, 40 min from each six sample schools) were observed. Besides one focus group discussion held with voluntarily selected teachers (one from sampled teachers in each school) and one focus group discussions held with voluntarily selected students (one from sampled students in each school) were used to study actual classroom teaching and learning of mathematics. It
provide both teachers and students with the opportunity to express their views precisely on challenges of implementing active learning strategies in Mathematics teaching and learning.
Although, both teachers and students questionnaires were adapted from different sources and modified for the current study, before they were utilized for the actual data collection in the schools, the researcher made a pilot study on 20 students at one primary school in other town. The overall Cronbach alpha reliability index was calculated and checked for the reliability. The relative specificity of the topics of the discussion and the experiences of the moderators in FGs satisfied the minimum expected reliability of the focus group discussion. Additionally, this instrument was validated in such a way that the participants discussed the questions accordingly during the group discussion. Furthermore, each of the instruments was validated in the other way. Before the actual data collection will start the instruments were given to colleagues so as to get valuable comments and criticisms on the strengths and weaknesses of the items. Based on the comments obtained, necessary modifications were made. Thus, answers to the written questionnaire, records of classroom observation checklist and focus group discussions were used to study actual classroom teaching and learning of mathematics.
Methods of data analysis
After collecting all the necessary data on each of the issues, the data was edited, coded, tabulated and processed in a way appropriate to answer the research questions. The quantitative data obtained from mathematics teachers and students through the questionnaires were analyzed by using frequencies, percentages and mean values using SPSS software. No hypotheses were tested as this is not the aim of the study. Teachers’ responses to the questionnaire on their practice of active learning methods (Section B, category 1 and 2) were used to answer research question one. The closed ended items w
as expressed in percentages and averages for the total score and discussed while the open-ended part was expressed and narrated qualitatively. The observation checklist data was analyzed by counting the scores of individual statements for the total of observed lessons and then expressing the counts in percentages. To supplement this result, the first parts of students’ responses were described using percentage analysis and the conclusion to research question 2 was reached.
Students’ responses to the second part of their questionnaire and the data collected from focus group discussion, and teacher’s questionnaire (Section B, category 3) was used to answer the third question of this research. The responses of the questionnaires were described using percentage analysis. The focus group data was read repeatedly and entirely transcribed. Then all the data in the form of transcripts were reviewed and carefully organized to identify the key themes using the coded key word approach and the results was described qualitatively. Finally, from the results, conclusions were made for each of the research questions and recommendations were forwarded.
Analysis of biographical data of teacher respondents
From the biographical data of teacher respondents, 19% of the teachers were between 30 and 39 and 23.8% of the teachers were between 40 and 49 years old. This implies that there are many teachers in the schools who are productive and young enough to serve in teaching profession. Majority (57.2%) of teacher respondents were above 49 years old which implies that they are almost to finish their working service and will left few years to retire. Of the teachers, 62% were male and 38% were female. This study therefore shows that the participation of females as mathematics teachers is medium when compared to the number of male mathematics teachers in the sample schools. Only 9.5% of the teachers have six to ten years of experience and are therefore relatively inexperienced. Also 9.5% of the teachers served eleven to fifteen years, while only 14.3% of the respondents worked for sixteen to twenty years and 66.7% of the teacher respondents taught for more than 20 years and are therefore experienced in the profession. 71.4% of the teachers were qualified in diploma and 28.6% of them have undergraduate degree in mathematics. This implies that hard work is required of the regional or zonal education bureau to develop and capacitate their primary school mathematics teachers.
Workload influences teaching style. In this regard, the biographical data indicates that only 76.2% of the respondent teachers had a workload of 15 to 20 periods (1 period is 40 min long) per week and 23.8% of the teachers have workload that ranges from 21 to 25 periods per week. The implementation of active learning approaches requires a certain amount of time to think about and explore each topic. Such approaches may take more time than a lecture. The aforementioned is complemented by the qualitative data. Classroom observation also indicated that the classroom seating arrangement does not allow teachers to employ active learning approaches comfortably. During FGs some respondents complained that the large class sizes did not allow them to change this type of seating arrangements and it also had a great impact on the implementation of active learning approaches. Most teachers (66.7%) replied that a typical classroom generally has more than 69 students. This was confirmed by classroom observations: The researcher observed 60 to 75 students in any given class.
Teachers use of different types of active learning methods
Using questionnaires supported by classroom observation and FGs, teacher’s provision of students with opportunities to actively participate in the use of active learning methods and the types of active learning methods used by the teachers during their mathematics classroom instruction were described.
From Table 1 above, teaching methods such as gap-lecture, individual work, questioning and answering and group work/discussion that seem to be participatory were observed (66.67%), however, when they were examined closely, they were not strong enough. For instance, questioning and answering activities were merely promoting “simple recall” or “comprehension” aspects of the cognitive domain. It was also noted that group works and discussions were not well-structured by teachers even though some teachers were tried to check dominant students answers in the group (50%).
From the lesson observations, again, it was ascertained that half of the teachers (50%) were checking students’ understanding throughout the lesson using different assessment techniques such as oral question, observation of students work, physical response and peer check. So generally, the methodologies used in the class were active but not properly applied because of some challenges such as large class size (teachers FGs), lack of necessary materials (students and teachers FGs and problems of classroom management (LO&TQ). Again the lesson observation results also revealed many of the students in four of the classes observed (66.67%) were not actively engaged in the given activities both physically and mentally. Half of the observed teachers were not encouraging passive students to participate in-group work. Even though many of the students responded to posed questions in many (66.67%) classes observed with their own words from their mind, a small number of students ask questions in many (66.67%) of the observed lessons. On the other hand, in the FGs for students, the sampled students expressed that they would enjoy the subject and learn them better if they had chance to like working on practical activities and real-life related problems. However, according to the students, the current classroom teaching learning situation did not promote this, because it had very little practical work because of shortage of time large class size.
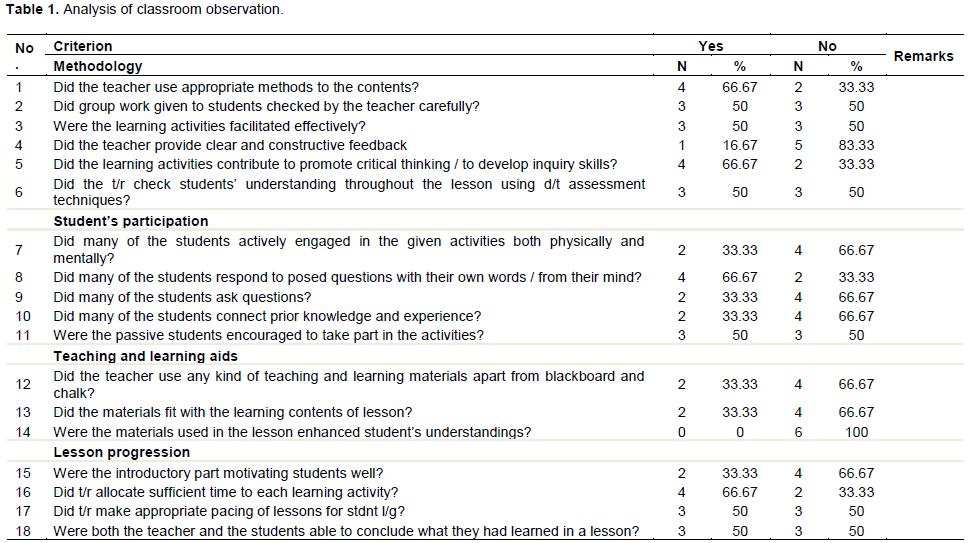
Regarding the teacher’s use of teaching and learning aids, from the six teachers observed, two teachers used teaching and learning materials apart from blackboard and chalk. The teachers ordered students to use a ruler and protractor to sketch and measure angles, but group dominant students performed the task. The teachers also accepted the correct answer of fast students from the groups but did not check the other students’ response for the given activity. The materials used in the lesson enhanced the student’s understanding. The progress of the lessons observed in all the classes was very good except the introductory part of many lessons (66.67%) were not motivating students well because the teachers went directly to presentation of the day’s lesson.
Regarding formation of group for team work, an item number one stated: “I rarely arrange the students into groups for mathematics team work.” Table 2 shows that 61.9 % (19.0%+42.9%) of the teachers disagreed and 37.6 %( 28.1%+9.5%) of the teachers agreed with this statement. On item number five, which states, cooperative work in groups is good for efficient learning, 38.1% teachers also agreed. Accordingly, they responded positively on the item that stated a cooperative learning is needed to help the students understand new concepts (Item 9). So many teachers (81%) thought that discussions between the students on a given lesson topic are vital for deep understanding (Item 10). Many students (25%) also stated in their questionnaire that their teacher often facilitated their learning rather than their own teaching in the class. This shows that the teachers realize that lecturing alone is not enough to prepare students to understand their lesson and hence, they support students to work in groups and learn cooperatively in mathematics classes.
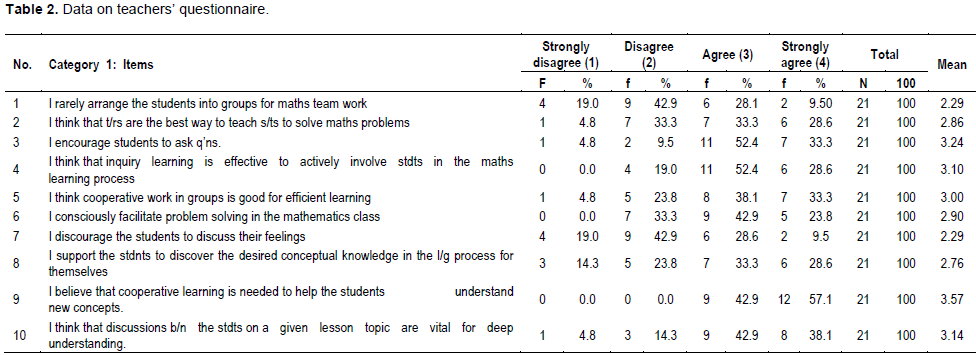
On the item four, if inquiry learning is effective to actively involve students in the mathematics learning process, 52.4 and 28.6% of teachers agreed or strongly agreed (mean value, 3.1). This is in line with item six that stated facilitation of problem solving in the mathematics class: About 66.7% (42.9 and 23.8%) of teachers showed their agreement (mean value of 2.9). However, the researcher observed that only fast learners were helped by the teacher to solve problems in the classrooms. This was confirmed by the FGs that indicated most of the time, fast learners only helped in problem solving and inquiry learning in mathematics classes.
Problem-solving skill is not only helpful in dealing with mathematics problems but also critical to solving the real-life situations, which we encounter in our daily lives (Morgan, 2007). Most of the teachers thus seem to realize the importance of active, discovery learning rather than thinking themselves as the best way to teach students to solve mathematics problems (item 2). Regarding discouraging students to explore their feelings and beliefs (Item 7), about 61.9% (19.0 and 42.9%) disagreed and 38.1% (28.6 and 9.5%) agreed. Therefore, many teachers (85.7%) encourage students to ask questions (Item 3). This seems to indicate that most teachers believe that lecturing alone is not enough for learning well. Many students (45.28%) also recognized in their questionnaire that their teacher often made them to show their solutions to the whole group and discuss any differences among the solutions (Table 3, Item 5). For item number eight of Table 2, the majority of the respondent teachers (33.3 and 28.6%, mean 2.76) indicated that they supported students to discover the desired conceptual knowledge in the learning process for themselves. This result is confirmed by lesson observation as the sample shown in Figure 1. However, observation confirmed that in some of the cases the role of the students was to listen carefully to the teacher’s lecture and writing notes from the blackboard. The role of some students was to memorize the facts and rules lectured on and to implement them (one student said in FGs). In addition, few students seemed to prefer to work individually in class. It was observed that in group work there were some students who did not do their share of the work.
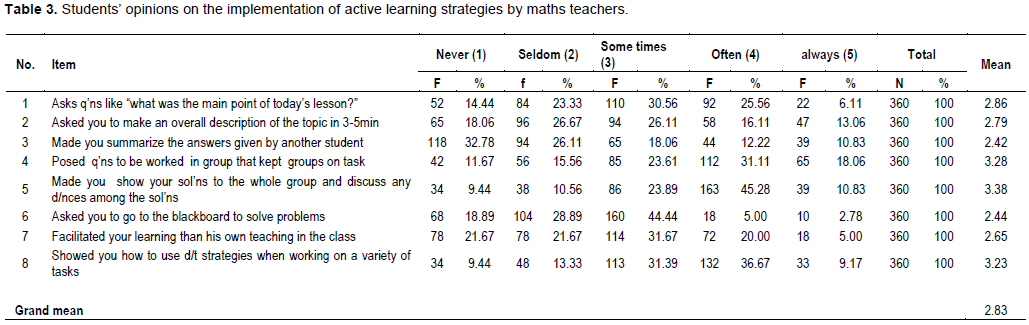

As shown in Table 3, 30.56% of students said their teachers asks them questions like “what was the main point of today’s lesson?” sometimes and 32.78% of the students said that their teacher never made them summarize the answers given by another students (Item 3). Besides 11.67% of students said that their teacher never posed questions to be worked on in the group that kept groups on task and also do not ask them (18.89%) to go to the blackboard to solve problems. 36.67% of students said their teacher often showed them how to use different strategies when working on a variety of tasks and 9.44% of students blamed their teacher concerning this aspect. Considerable amount of student respondents (23.61%) said they never were provided with multiple opportunities to practice the skills being taught by their mathematics teachers. 62.8% of students replied to the item “Do your teacher connected the topics being covered to your daily life?” positively where as 37.22% of respondents replied negatively to this item.
The results of this study indicate that the teachers’ implemented active learning/student centered approaches at various stages of the instructional process to some extent (Grand mean 2.83 and 2.9). Active learning approaches such as the inquiry method, group work/discussion, gap lecture, cooperative learning, and individual work, which foster the critical thinking of students, were the methods used commonly by the teachers (Table 4).
We as teachers have typically suspected - students can often do the mechanical things we ask with certain content/topic but there is not always a high level of understanding behind these computations (Melaku and Solomon, 2013). In active learning classrooms, students are engaged in activities like dialogue, debate, writing, discussion and problem solving as well as higher order thinking such as analysis, synthesis and evaluation.
In the teaching learning process, lessons can be divided into: Starting phase (summarizing work covered in previous lessons); new content introduction phase, central phase (explanation of the content); activities phase (students work on the content); closing (final feedback) phase. The classroom observations showed that many of the phases, with the exception of central phase, are student-centered approaches. Further, some students in the observed classes were responsible only to listen to lectures, take notes and respond to questions upon request. This is associated with the students’ prior experience of active learning, as pointed out by most of teachers in the FGs. Students have no experience to play the active roles expected of them because many come from authoritarian cultural backgrounds and therefore talk only when motivated by someone. Discussion methods help to facilitate active learning/student-centred approaches, as indicated by the work of Baines et al. (2007). However, a number of the teachers said that interaction occurred more easily in a relatively small class size (Teacher’s FGs).
Most participants in FGs also commented on improper use of active learning approaches in their teaching practice. Some said that any transformation from a teacher-centred classroom to an active learning/student-centred classroom, since it involves fundamental change, will meet with resistance. In contrast, a number of teachers noted that it was an approach they already used, had used for a considerable time, or was an implicit part of teaching their mathematics subjects.
Challenges of using ALMs and supports provided for its implementation
Using questionnaires supported by classroom observation and FGs, the factors that hindered the implementation of active learning approaches in the sample schools (Tables 5 and 6) were determined. Table 5 shows data collected from students’ questionnaire on factors hindering the implementation of active learning approaches. As indicated by the percentages and means in the table, the following were mentioned as the major factors: Students do not want to talk about the lesson during teaching learning process (79.72%); Lack of necessary materials (e.g. papers, diagrams…) (64.44%); many of the time, teacher use lecture method in the class. (61.11%); Shortage of time in the classroom (49.44%); Teachers did not control the group learning activities (41.66%); teachers’ negligence in participating students in the class (36.11%).
Table 6 shows teachers’ responses on factors Hindering the implementation of active learning approaches. The result shows that active learning demands too much effort from teachers (90.48%); there is a lack of time to actively involve students in my classroom teaching (80.95%); to involve students in active learning will add too much to my work load (66.67%); active student learning will create problems in my classroom management (61.9%); the amount of content that needs to be covered prevents the use of active learning in the classroom (61.9%). During the FGs of teachers, teacher participants were asked: What are the factors/challenges that limit you in applying different active learning methods in teaching mathematics at your school? Teachers’ responses focused on lack of necessary materials, classroom conditions and shortage of time. Examples include:
Theoretically active learning is very useful, but practically difficult to apply for a number of reasons like large class size, work load of teachers, lack of teaching materials, and lack of interest and some complaints of both the teachers and students…
Here, the results of the study are discussed regarding teachers’ use of active learning/teaching methods in class and major factors affecting the implementation of active learning approaches.
Teachers’ use of active learning in the teaching-learning process
Many educators describe the constructivist approach to learning as a process where by students work individually or in small groups to explore, investigate and solve authentic problems and become actively engaged in seeking knowledge and information. In active learning approaches, students participate actively in their learning and become autonomous learners who actively construct new meaning within the context of their current knowledge, experiences and social environments. Active learning gives students the opportunity to learn through their own efforts and to take full responsibility for their own learning with the teachers as facilitators (Berhanu, 2010).
The results of this study indicate that schoolteachers implemented active learning approaches at various stages of the instructional process to some extent. It is not only teachers’ that affect the implementation of active learning approaches. Students also affect how learning is practiced and how teaching is organized. In the FGs, some teachers complained that some students had negative attitudes towards active learning approaches. It is known that learning is active when students take the initiative and responsibility for their own learning and this is dependent on students ‘positive attitudes. This is not the case in the sample schools, where observation indicated that some of the teachers mainly used lectures to teach students to solve mathematics problems and they rarely arranged the students into groups for mathematics teamwork. This may be caused by large class sizes. Table 2 also shows that majority of the sample teachers (62%) thought that teachers should decide the best way to teach students to solve mathematics problems. However, students build and share their own knowledge with others when they interact with each other and with their teachers (Zweck, 2006). Furthermore, active learning/student-centered approaches such as the inquiry method; problem solving and discovery methods, which foster the critical thinking and problem-solving capacity of students, were not widely employed. In this regard Balım (2009) emphasizes that students should do more than just listen. They need to read, write, discuss or engage in problem solving activities. In active learning classrooms, students are engaged in activities like dialogue, debate, writing, discussion and problem solving as well as higher order thinking such as analysis, synthesis and evaluation. In the teaching learning process, lessons can be divided into: Starting phase (summarizing work covered in previous lessons); new content introduction phase, central phase (explanation of the content); activities phase (students work on the content); closing (final feedback) phase. The lesson observations showed that all the phases, with the exception of central phase which takes more than half of the time, are student-centered approaches. It was also observed that the teachers frequently asked low-level order questions and only a few students try to answer. This is also supported by the result obtained from the student’s FGs by indicating that their teacher asks oral questions many times and
even give the answer himself.
Further, a number of students in the observed classes were responsible only to listen to teachers, take notes and respond to questions upon request. This is associated with the students’ prior experience of active learning, as pointed out by most of teachers. Students have no experience to play the active roles expected of them because many come from authoritarian cultural back-grounds and therefore talk only when motivated by someone. Teachers do not take this into consideration when they encourage student participation in instructional processes. This is confirmed by the classroom observation and FGs of teachers.
Discussion methods help to facilitate active learning/student-centred approaches, as indicated by the work of Baines et al. (2007:674-676). Discussion can help to develop improved cognitions. Most of the teachers stated that discussion was important. However, a number of the teachers said that interaction occurred more easily in a relatively small class. In summary, in the sample schools instruction/teaching-learning was mixed (both teachers and student centered) instruction. However, research shows that learning is enhanced in contexts where students have supportive relationships, have a sense of ownership and control over the learning process, and can learn with and from each other in safe and trusting learning environments (McCombs, 2003).
The major factors/challenges influencing the implementation of ALMs
According to FGs, many teachers believed that lack of classroom space and large classes prevented group work. In addition, the following prevented active learning: Lack of time to actively involve students in teaching; the amount of content to be covered; lack of resources; lack of instructional materials; lack of administrative support; and that is took too much effort from teachers. This was confirmed during FGs of teachers and students.
According to Weimer (2002), for the effective implementation of active learning/student-centered approaches the principals and department heads of the school also need to recognize active learning approaches as building blocks forlifelong learning and provide the support required from them. However, in this study lack of administrative support and lack of resources inhibited the implementation of active learning in class.
As mentioned, content coverage was a high priority for teachers. Although some teachers indicated that they covered some or most content with active learning approaches, other adopters of active learning approaches indicated that they covered less content than when they lectured exclusively, but that students were learning more. Silberman in Zweck (2006) showed that students in contexts in which teachers paused at intervals and talked six minutes less performed significantly better on the same examination than students in contents where teacher lectured the entire time. Time was an issue. Based on their experience, a large number of teachers thought that active learning would take up more time than the traditional way of teaching. Some teachers believed that due to time constraints, active learning could not be applied in a short period. They also believed that the students were passive and that it took a long time to motivate them. The curricular materials and classroom environment were also factors that played a role (FGs of teachers). For active learning, the materials should include carefully sequenced sets of guiding activities designed to be performed actively by the students. However, as shown by responses from the majority of teachers and as observed, the activities during instruction were not presented in a way to encourage independent, purposive and a reflective way of learning. As mentioned by Feden and Vogel (2003), active learning and teaching materials should contain plenty of exercises and samples of work. They should also be flexible and allow students the time to work at their own pace and using their own methods. But in the present study, teaching materials were filled with large amounts of information to be memorized by the students. Thus, many teachers felt responsible to cover the curriculum in the time provided by a rigid time table. Class size was also a factor. McKeatchie and Svinicki (2005) stated that in a large class, individualization of instruction is limited.
FGs also indicated that a factor that influences the implementation of the approach is interpersonal relationships or interactions among individuals. Active learning approaches are characterized by “empathic, supportive relationships which free students to discuss their feelings and experiences” so that students are “actively involved in learning through the given opportunities to predict, infer, generalize, and evaluate” (Duffy and Kirkley, 2003). The role of the students in active learning approaches is learning by doing. So as to engage students in learning activities, the classroom should be well equipped with the appropriate furniture and there should be movable desks for every student to use in different layouts in the classroom. From this point of view, the arrangement of desks and tables should allow movement and communication and should be changed whenever necessary. Furthermore, ample teaching resources should be available to implement active learning approaches as required. In this regard, the majority of student respondents (64.4%) replied that they were constrained by lack of adequate resources for using active learning approaches (Table 6). The data obtained from classroom observation show that some of the classroom seating (the front to back arrangement) does not allow teachers to employ active learning approaches. The desks and tables in most of the classrooms were heavy and could not easily be moved.
Mathematics teachers of the sample schools encouraged students to ask questions; to deduce general principles from practical exercises and facilitate some problem solving in the mathematics classes. Besides, some teachers commonly used active learning methods such as the inquiry/questioning method, group work/ discussion, cooperative learning, individual work and discovery methods. The basic active learning activities that were not implemented by most of the observed teachers in the sample schools include physical activities such as hands on projects, manipulative, using cooperative groups for problem solving activities; and facilitating students’ curiosity/interest. The inadequate use of the different active learning methods would negatively influence the quality of the teaching-learning process; negatively affect development of self-learning, higher order thinking and problem solving capacities among the students. In this regard the researcher support active learning as pedagogical approach but teachers need to be aware of the constraints that they may face. By incorporating carefully selected intellectual, social, and physical activities into the their classroom, teachers can meet the unique developmental needs of young students while teaching the important content these students need to learn to be empowered to think critically about the world around them. Active learning helps teachers modify their traditional roles and encourages them to conduct more student-centred applications. If a program is grounded in, or moving toward, a constructivist paradigm, active learning could be a valuable tool for helping teachers construct knowledge about teaching and learning. Teachers should have a more active role as developers of teaching, and they are seen as being more responsible for the development of their own profession in a larger sense.
Teachers’ culture should provide more active learning experiences to prepare them to use new methods with their students in schools. Thus, they should be qualified and must be well prepared, especially in improving the quality of education that faces global challenges.
I would like to thank Jimma College of Teachers’ Education for the financial assistance of this work. I am grateful to all mathematics teachers and school leaders at Woliso town second cycle elementary schools for their cooperation during data collection. My special thanks go to my friends Alemayehu Leta and Dinaol Tariku for their concern in helping me to collaborate for data collection. Finally, my friends and colleagues such as Abadir Ibrahim, Bekalu Ferede and Behailu Etana for their unreserved guidance and constructive comments throughout the development of this study.
The author has not declared any conflict of interests.
REFERENCES
|
Baines E, Blatchford P, Chowne A (2007). Improving the effectiveness ofcollaborative group work in primary schools: effects on science attainment. British Educational Research Journal 33(5):663-680.
Crossref
|
|
|
|
Balım AG (2009). The effects of discovery learning on students' success and inquiry learningskills. EgitimArastirmalari-Eurasian. Journal of Educational Research P 35.
|
|
|
|
|
Berhanu M (2010). Active Learning Approaches in Mathematics Education at Universities in Oromia, Ethiopia. School of South Africa.
|
|
|
|
|
Bonwell CC, Eison JA (1991). Active learning: creating excitement in the classroom. ASH#-ERIC Higher Education Report No. 1, Washington, D.C.: The George Washington University, School of Education and Human Development.
|
|
|
|
|
Borkowski JG, Muthukrishna N (1992). Moving metacognition into the classroom: Working models and effective strategy teaching. In: Pressley M, Harris KR Guthrie JT (Eds.), Promoting academic competency and literacy in schools. San Diego, CA: Academic Press, Inc. pp. 477-501.
|
|
|
|
|
Bransford JD, Brown AL, Cocking RR (1999). How people learn: Brain, mind, experience, and school. Washington, D.C.: National Academy Press.
View
|
|
|
|
|
Burns C, Myhill D (2004). Interactive or inactive? A consideration of the nature of interaction in whole class instruction. Cambridge Journal of Education 34(1):35-49.
Crossref
|
|
|
|
|
Duffy TM, Kirkley J (2003). Learner-centered theory and practice in distance education: Cases from higher education. Routledge.
Crossref
|
|
|
|
|
Feden P, Vogel R (2003). Methods of teaching: Applying cognitive science to promote student learning, McGraw Hill Higher Education. Implementing active learning.
|
|
|
|
|
Gay LR Airasian P (2000). Educational research: competencies for analysis and application. Sixth Edition. New Jersey: Merrill Prentice- Hall. L
|
|
|
|
|
Larsson S (1983). 'Paradoxes in teaching', Instructional Science 12:355-365.
Crossref
|
|
|
|
|
McCombs BL (2003). Applying educational psychology's knowledge base in educational reform: From research to application to policy. In WM. Reynolds GE. Miller (Eds.) Comprehensive handbook of educational psychology. New York: Wiley 7:583-607.
|
|
|
|
|
McKeachie WJ, Pintrich P, Lin Y, Smith D (1986). Teaching and learning in the college classroom: A review of the research literature. Ann Arbor: University of Michigan, NCRIPTAL.
|
|
|
|
|
McKeachie WJ (1999). Peer learning, collaborative learning, cooperative learning, in Teaching tips: Strategies, research, and theory for college and school teachers, 10thEdition. Boston: Houghton Mifflin pp. 158-166.
|
|
|
|
|
McKeatchie W, Svinicki M (2005). Teaching tips: Strategies, research, and theory for college teachers. 12th Edition. Boston: Houghton Mifflin.
|
|
|
|
|
Meyers C, Jones TB (1993). Promoting active learning: Strategies for the college classroom. San Francisco: Jossey-Bass.
|
|
|
|
|
Melaku T, Solomon A (2013) Teaching and Learning of Trigonometry: Misconceptions and Difficulties. Deutschland/Germany; Lap Lambert Academic Publishing.
|
|
|
|
|
Morgan MK, Clarke RM, Weidmann M, Laidlaw J, Law A (2007). How assessment drives learning in neurosurgical higher training. Journal of Clinical Neuroscience 14:249-354.
Crossref
|
|
|
|
|
Ministry of Education (1994). Education and Training Policy, Addis Ababa; St.George Printing Press.
|
|
|
|
|
National Council of Teachers of Mathematics (NCTM) (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
|
|
|
|
|
Penner J (1984). Why Many College Teachers Cannot Lecture: How to Avoid Communication Breakdown in the Classroom. Charles C. Thomas, Publisher, 2600 South First Street, Springfield, IL 62717.
|
|
|
|
|
Rutherford FJ, Ahlgren A (1990). Science for All Americans; New York: Oxford School Press.
|
|
|
|
|
Saljo R (1979). Learning in the learner's perspective: I. Some common-sense assumptions." Reports from the Department of Education P 76.
|
|
|
|
|
Slavin R (2005). Educational psychology. 7th Edition. Boston: Allyn. Bacon.
|
|
|
|
|
Stuart J, Rutherford R (1978). Medical student concentration during lectures. Lancet 23:514-516.
Crossref
|
|
|
|
|
Thomas LF, Harri-Augstein ES (1985). Self-organized learning: Foundations of a converstational science for psychology. London: Routledge.
|
|
|
|
|
Verner C, Dickinson G (1967). The lecture: An analysis and review of research. Adult Education 17:85-100.
Crossref
|
|
|
|
|
Weimer M (2002). Learner-centred teaching: Five keys changes to practice. USA: Jossey-Boss.
|
|
|
|
|
Wiske MS (1998).Teaching for Understanding. Linking Research with Practice. The Jossey-Bass Education Series.
|
|
|
|
|
Zweck J (2006). Strategies to promote active learning in math/stat discussion sessions.
|
|