ABSTRACT
Pattern activities have a crucial role in supporting early academic and language skills related to cognitive development, as they play a key role in understanding mathematical ideas and relationships, and in understanding the order, logic and concepts of mathematics. From this point of view, the research was conducted to investigate the effect of the Pattern-based Mathematics Education Program on the early academic and language skills of 61-72-month- old preschoolers. Quasi-experimental design with pretest-posttest control group was used in the study. Forty children, 20 for the experiment and 20 for the control group, constituted the sample. In the experimental and control groups, there were 61-72-month-old children who had not received any special mathematics education and were showing normal developmental characteristics; while attending one of the pre-school education centers in two different campuses of a public university in Besiktas and Esenler districts in the city of Istanbul, Turkey. In the study, General Information Form and Kaufman Survey of Early Academic and Language Skills” were used as data collection tools. A total of eight weeks 'Pattern-based Mathematics Education Program' was applied to the children in the experimental group, five days a week. Kaufman Survey of Early Academic and Language Skills was administered as pre-test and post-test to the experimental and control groups. The same test was given to the experimental group as retention test three weeks after the post-test. In this study, which was limited to the activities presented in the Pattern-based Mathematics Education Program, it was determined that the Pattern-based Mathematics Education Program was effective in supporting the early academic and language skills of 61-72 month old preschoolers.
Key words: Pattern skills, early academic and language skills, early mathematics education, early childhood education.
The essence of mathematics lies in relationships and transformations that lead to patterns and generalizations (Warren, 2005). Mathematics, while investigating and reasoning the accuracy of claims about relations between
objects (Carpenter, et al., 2003), plays a key role in finding out the pattern, mathematical ideas and relationships while providing and understanding of the order, logic and concepts of mathematics (Burns, 2015; Hargreaves et al., 1998). Therefore, mathematics can be named as the science of patterns (Lan-Ma, 2007). Pattern has been defined as noticeable levels of powerful arrangements with numbers, words and figures (Birken and Coon, 2008); the number associated with each other is defined as the fact that space or measurement variables contain predictable regularity (Mulligan and Mitchelmore, 2013). At this point, patterns emphasize the existence of an order and rule in mathematics (Billstein et al., 2016).
The patterns are grouped into three main categories: repeating, growing and relationship (Smith, 2009). Repeating patterns are divided into three groups: linear, circle and hopscotch (Papic, 2007). The changing patterns are grouped in three ways as fixed, increasing and decreasing (Olkun and YeÅŸildere, 2007). On the side of individuals, patterns are discovered in four stages: recognizing the pattern, defining the pattern, continuing the pattern and producing a new pattern as the final stage (Copley, 2000; Smith, 2009). Steps such as recognition, continuation and creation of patterns are very important capabilities in seeing mathematical relations, making generalizations and understanding the layout of mathematics (Burns, 2015). For this reason, the National Council of Teachers of Mathematics [NCTM] (2000) suggests that children should be able to make advanced generalizations by emphasizing the development of reasoning in terms of geometric and numerical patterns, and to make pattern activities in which they can present patterns in verbal, tabular and graphical form. In Turkey, the Ministry of Education Pre-School Education Program (2013) children are expected to gain skills in supporting their cognitive development by "creating a pattern with models looking at the object, saying the rule in the resulting pattern of at most three elements, saying the item left missing in a pattern, completing or creating a unique pattern with objects". Papic et al. (2011), in their study investigating the patterning strategies of children from 3 years and nine months to five years of age, found that children were successful in recognizing patterns in various spatial patterns even at very young ages. In early childhood, children can easily participate in pattern activities in mathematics, science, music, movement and art sessions by using real objects, themselves and pattern cards; thus they gain experience in patterns. With the help of such process, children are able to notice, identify, continue the existing pattern and produce a new one (Charlesworth and Lind, 2007; Copley, 2000; Smith, 2009).
If children experience the activities related to the pattern from the early period, it can be seen that they begin to perceive patterns indirectly around two years. They can define simple patterns at the age of three and can place the appropriate element to the space in the repeating pattern of two units. At the age of four years, two-unit repetition pattern can be copied and expanded without looking at the model. They can expand simple repetition patterns at five years of age. At the age of six, they define the smallest repeating unit in the repeating pattern, and at seven years of age, they can explain the number patterns and translate it into geometric or numerical representations (Sarama and Clements, 2009). This developmental process also contributes to the development of algebraic and functional thinking in children (Copley, 2000; Smith, 2009). Pattern activities also contribute to the development of skills such as sequencing, and basic numerical processing (Papic and Mulligan, 2005) and in the development of cognitive abilities such as reasoning, communication, association and problem solving (Papic and Mulligan, 2005; Warren and Cooper, 2006). Children explore mathematical concepts while working with pattern activities (Charlesworth and Lind, 2007; Copley, 2000) and can judge the relationship between variables in patterns (English, 2004). Apart from these, the patterns also provide a sense of number. Repetition patterns are seen as a prerequisite for number theory and generalization (Smith, 2009). A child who perceives the repetition unit can start the algebra, which is isolated from a concrete situation, by analyzing the numbers and the relations between them (Charlesworth and Lind, 2007; Copley, 2000; Smith, 2009). Since algebra studies of numbers and arithmetic can improve both the arithmetic and algebraic reasoning of children, it can facilitate the development of a positive tendency for mathematics problems from early ages (Diezmann et al., 2001). Therefore, the importance of patterns in the discovery and understanding of mathematical concepts in pre-school period is great.
In the context of early literacy skills that constitute another sub-field of academic skills, skills such as verbal language skills and articulation, alphabet knowledge, phonological awareness and writing skills are included ( Neuman and Dickinson, 2002). In the definition of patterns, there is an identification status with the process of auditory, visual and psychomotor discovery (Charlesworth, 2000: 190 as cited in Waters, 2004). Specifically, the identification of patterns with the audio-visual and visual exploration process can be considered within the scope of early literacy skills. Music patterns in the form of lullabies, lyrics or melodies created in line with the successive sounds or words within the patterns (Geist et al., 2012) can support the increase in children's capacity to understand patterns not only visually but also auditory (Zentner and Eerola, 2010). Regular repetition of lullaby, rhyme, lyrics or melodies can improve children's various concepts, affective and language development, and motor skills (Gök Çolak, 2016). Considering the concept of pattern as an intertwined concept of music and using music patterns in mathematical pattern studies (Edelson and Johnson, 2003; Geist et al., 2012; Zentner and Eerola, 2010) can help children’s development of their basic sound, intonation and rhythmic vocabulary. In addition, children gain intonation and rhythm skills in parallel with the development of speaking, listening, speaking, reading and writing skills (Etopio, 2009).
In the literature, it is observed that researches with preschoolers in terms of pattern skills are rare; nevertheless, Papic (2007) found that most of the children were able to construct, expand, describe, and verify patterns because of the interviews with children who had been attending to kindergarten for two years and had never experienced any growing patterns. Papic (2015) developed the Early Mathematical Patterning Assessment (EMPA) scale which aims to measure mathematical thinking and patterning skills of children aged between four and five years. Warren (2005) aims to reveal how young children generalize repeating and changing patterns and how they symbolize these generalizations. On the other hand, KesicioÄŸlu (2013) examined mathematical pattern skills of preschoolers in terms of various variables. In addition, two studies investigating the effect of educational activities related to the concept of pattern including games and books in order to increase the level of knowledge and experience of preschoolers in terms of pattern skills were found (Gök-Çolak, 2016).
While there are studies examining patterns and supporting early language skills and academic achievement, no studies in Turkey have been found specifically examining the impact of pattern activities on preschoolers’ academic and language skills addressing these skills as a whole. In recent years, the study of alternative approaches to support early academic and language skills and deficiencies in the creation of pattern-based educational programs reveal the importance of this research. At the same time, it is thought that pattern-based mathematics education program will be helpful in giving teachers a different perspective and will contribute to the studies in this field. In this context, the main hypothesis was determined in this study, which was conducted to investigate the effect of the Pattern-based Mathematics Education Program on early academic and language skills of 61-72 month old preschoolers:
"Is there a significant difference (p<0.05) between the children in the experimental group in which the Pattern-based Mathematics Education Program is applied and the posttest scores of the children in the control group in which the current education program is applied in terms of vocabulary, numbers, letters, words and articulation subtests”?
Research design
In order to investigate the effect of Pattern-based Mathematics Education Program on early academic and language skills of 61-72 months old preschoolers, quasi-experimental design with pretest- posttest control group was used. Since it is difficult for children to be assigned to groups as neutral in educational settings, quasi-experimental designs are preferred in which groups can be matched from certain variables (Gay et al., 2005). Therefore, quasi-experimental design was used in this study. In the study, 2x3 mixed patterns including pre-test, post-test and retention test were used with the experimental and control groups. In the mixed design (Split-plot factorial design), there are at least two variables of which effect is examined on the dependent variable. One of them defines the different experimental process conditions formed by the neutral groups and the other defines the repetitive measurements of the subjects at different times (pre-test, post-test, retention test) (Büyüköztürk et al., 2011). In this study; between-groups variable defines “experimental and control groups” within-groups variable defines “pre-test, post-test, retention tests”.
Sampling
In the study group of the research, the preschool education institutions of the universities were listed first. The schools in the list were examined by the researchers and interviews were made with the school administrators and kindergarten teachers and information was taken on whether a special training program was applied on any subject. According to this, preschool classes on which no specific education program had been implemented were listed. In addition, care was taken to ensure that the children included in the study group were willing to participate in the study by obtaining parental consent. According to this, K1 Preschool Education Unit, which is not included in any education program determined by purposive, sampling method, which is in the campus of a state university volunteering to participate in the research, as experimental group. The K2 Preschool Education Unit, located on the other campus of the same university, was also selected as the control group. The study group included 20 children (6 girls-14 boys) in the experimental group and 40 children (11 girls- 9 boys) in the control group.
In the research, 30% of the children in the experimental group were girls and 70% were boys; 35% were first child, 15% were the middle child, 50% were the last child. It is seen that 35% were the only child and 65% had 1-4 siblings. 55 and 40% of the parents of the children were 39 and under, respectively; 45 and 60% were 40 and over, respectively. Twenty percent of parents had high school and lower degree, 35% had bachelor's degree and 45% had master's degree.
Fifty-five percent of the children in the control group were female and 45% were male. It was seen that 50% were the first child, 5% were the middle child and 45% were the last child. Sixty-five of the parents and 55% of the parents of the children were 39 and under; 35 and 45% were 40 and over. Twenty-five of the mothers of the children had high school or lower degree, 65% had bachelor's degree and 15% had master's degrees, while 25% of the fathers of the children in the control group had high school and lower degree, 55% had bachelor's degree and 20% had master's degree.
In order to test the effectiveness of the method / program applied in experimental studies, it is necessary to determine whether there is a significant difference between the groups in terms of the effect of the groups on the effect investigated (Heppner et al., 2008).
Table 1 shows that there was no statistically significant difference according to the results of Kaufman Survey of Early Academic and Language Skills of children in the experimental and control groups as pre-test: Vocabulary (U = -0.628, p> 0.05), Numbers, Letters, Words (U = -0.177, p> 0.05) Articulation Survey (U = -0.163, p> 0.05), K-SEALS (U = -0.136, p>0.05). According to this result, it can be said that the experimental and control groups had similar characteristics in terms of early academic and language skills. This also shows that the experimental and control groups were homogeneous.
Data collection tools
In the study, in order to collect demographical information about the children “Personal Information Form” and Kaufman Survey of Early Academic and Language Skills (K-SEALS) to test the children’s early academic and language skills were used.
Personal information form
In order to collect personal information about children, a personal information form, which was developed by the researchers, was used to collect information such as birth date, gender, number of siblings, age of parents, and level of education. Personal information forms were filled by the researchers for each child depending on the information in the personal development files of the children in schools.
Kaufman survey of early academic and language skills - K-SEALS
Kaufman Survey of Early Academic and Language Skills original form was developed by Kaufman and Kaufman (1993) and provides assessment of early language, cognitive competence and academic skills of children aged 36-83 months. K-SEALS consists of three sub-tests, four sub-tests, and an Early Academic and Language Skills Composite, which includes the children's early academic and language skills, Word Knowledge, Numbers, Letters and Words and Articulation Survey. It is applied in a quiet and comfortable environment. When the test is applied, each item illustration in the easel is shown to the children, the instruction of the item is read aloud and expected to be answered by the children. For each correct answer, one score is recorded in the test registration form and zero (0) point for each incorrect answer. The test consists of 90 items and it took 15-25 min for each child to apply. The raw score for each subtest is the number of items correctly answered (Kaufman and Kaufman, 1993). In Turkey Uyanık and Kandır (2014) adapted K-SEALS according to the Turkish children and confirmatory factor analysis according to the total it was determined the one-dimensional factor structure was verified. The KR-20 reliability coefficient for K-SEALS was found to be 0.971 and the item total correlation coefficient of the majority of the items was at a high level of reliability. The test retest correlation for K-SEALS total was set at .908. The relationship between the two test results was found to be significant at p <0.01 level. The researchers individually in a quiet environment administered the test with each child.
Pattern-based mathematics education program (PMEP)
In the Pattern-based Mathematics Education Program, 61-72-month-old children were taken as a basis to raise awareness about the concept of pattern. The philosophy of the program was primarily based on the different views and approaches of theorists such as Rousseau, Montessori, Piaget, Vygotsky, Gardner, Hebb and Dienes. At the same time, theoretical framework of the education program has been established by taking into consideration the literature related to pattern skills and programs implemented worldwide such as Montessori, High Scope, Regio Emilia, Waldorf and “The Big Math for Little Kids” (Balfanz et al., 2003), “Building Blocks” (Clements and Sarama, 2007), and “Number Worlds” (Griffin, 2004) and the gains and indicators included in Turkish Ministry of National Education Preschool Education Program (2013). Based on this, specific gains related to the pattern and which can be added to the program have been prepared. According to the theoretical framework, the program aims to contribute to the mathematical thinking skills by supporting the children's ability to discover, recognize, copy, find the unit of the pattern, continue the pattern and create a unique pattern. Children's sense of curiosity and discovery, and active participation in the program is considered as a whole including daily life, play and mathematics. This educational program that allows children discover patterns, repeat basic areas, including changing and relationship patterns and creating various learning experiences with different forms of activities such as number, shape, sound and movement. The activities in the program were prepared from simple to complex, from concrete to abstract, sequential and spiral by focusing on the developmental characteristics of children. In the program, children are encouraged to have an opportunity to gain awareness about the concept of pattern with their senses by discovering, recognizing and understanding the unnoticed patterns around them. At the same time, the implementation of pattern activities for various sense organs allows children to acquire skills such as conversion of patterns to different senses (audio-visual, visual-audio, etc.), as well as inter-dimension transformation (converting the three-dimensional pattern into two dimensions, etc.). Pattern-based mathematics activities are integrated with Turkish, music, play, science, movement, drama, reading, writing and art activities, aiming to improve the awareness of pattern and mathematics that exist in daily life and which are related to other disciplines. In addition, children are given the opportunity to work as individual, in small or large groups. The program was designed in accordance with the mathematical process standards including basic mathematical concepts and skills to be acquired in early childhood and in accordance with the development of cognitive abilities and integrated into Turkish Ministry of National Education Preschool Education Program. The Pattern-based Mathematics Education Program was sent to five field experts and finalized after the scope was validated. Pattern-based Mathematics Education Program consists of materials as follows: program summary, educator resource set, in-class educational activities, parent education activities, evaluation forms. The Pattern-based Mathematics Education Program consists of 40 activities for a period of eight weeks, five days a week. Approximately 20 min were spent for each activity. Twenty activities from the repetition pattern, which the children found easier, 13 activities from changing patterns and 7 activities from the relationship pattern, were prepared by considering developmentally appropriate practices. Within the scope of these types of activities, in 14 activities, there were number patterns, in 14 activities, there were shape patterns, in 12 activities there were sound patterns and in 8 activities there were movement patterns. Therefore, Pattern-based Mathematics Education Program is an educational program that allows children to use all their senses effectively with activities created in different forms, including sound, shape, number and movement. Implementation of pattern activities for various sensory organs allows the acquisition of skills such as changing patterns of different senses (audio-visual, visual-audio, etc.) as well as inter-dimensional conversion (conversion of three-dimensional pattern into two, etc.). For example, the educator prepares a circular track with the help of electrical bands consisting of a rectangle, circle and triangle-repeating units. Here, children are provided with opportunities for recognizing cyclical patterns and the repeating units. The educator asks the children to tell each name when it comes to each shape and to make the same shape with their hands. In this way, children turn patterns into movement as they describe their patterns verbally. In another activity, children are expected to make the pattern drawn on the paper with blocks or legos, wherein the skill of transforming of the two-dimensional pattern to three-dimensional is achieved. The pattern of the activity is given in Figure 1.
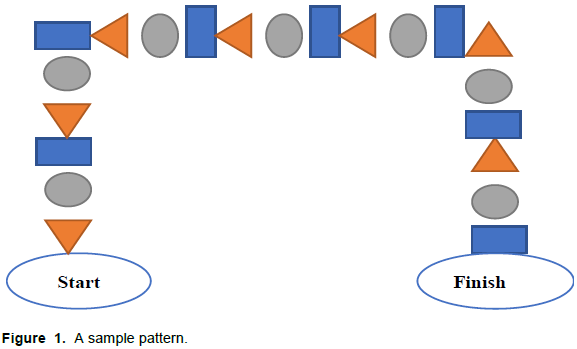
After the researchers administered the pre-tests, the teacher of the experimental group applied Pattern-based Mathematics Education Program to the children in order to eliminate the difference between the teacher and the researcher. During the pretest administration, the researchers provided information to the volunteer teacher who was in the experimental group regarding the characteristics of the Pattern-based Mathematics Education Program, gains and indicators in the program, arrangement of the learning environment, learning and evaluation processes in the program and the methods and techniques to be used during the implementation. The activities planned to be implemented were explained to the teacher in the experimental group by the researchers by organizing the educational environment one day in advance and the materials were explained together with their intended use. Furthermore, the teacher was informed about parent involvement activities, evaluation forms and how to implement educational processes. After researchers showed the implementation procedure to the teacher, the teacher was asked to apply the activities according to the steps in order, the activities were re-played under the supervision of the researchers, and it was role-played to be prepared for the actual implementation. The education program was implemented five days a week for eight weeks and feedback was given to the teacher after each application. In the control group, the kindergarten teacher in its natural flow implemented the program by continuing the implementation of the existing education program.
Data analysis
In the study, descriptive statistics such as frequency and percentage were used to evaluate demographic characteristics of children. Due to the normality test [Kolmogorov-Smirnoff (K-S)] of the scores obtained from Kaufman Survey of Early Academic and Language Skills, Mann-Whitney U Test was used for investigating the differences between groups and Wilcoxon Signed Rank Test was used for within group comparisons. While examining the differences between the groups; .05 was used as the level of significance and it was reported that there was no significant difference between the groups in the case of p>0.05.
The results of the research conducted in order to investigate the effect of Pattern-based Mathematics Education Program on early academic and language skills of 61-72-month-old preschoolers are presented in tables. Table 2 shows that the difference between the pretest and posttest scores of preschoolers attending the Pattern-based Mathematics Education Program in terms of the subtests of Kaufman Survey of Early Academic and Language Skills was significant (p<0.05) as follows: Vocabulary (z = -3.633), Numbers, Letters and Words (z = -2.933), Articulation Survey (z = -3.42) and K-SEALS Total (z = -3.737). It is observed that this difference was in favor of the posttest mean scores.
According to Table 3, the difference between the posttest and retention test scores of the experimental group children was not significant (p>0.05) in terms of the subtests of K-SEALS: Vocabulary (z=-1.457), Numbers, Letters and Words (z=-0.208), Articulation Survey (z=-0.597) and K-SEALS Total (z=-0.879).
Table 4 shows no significant difference (p> 0.05) between the pretest and posttest scores of children in the control group in terms of the subtests of K-SEALS: Vocabulary (z = -0.745), Numbers, Letters and Words (z = -0.592), Articulation Survey (z = -1.177) and K-SEALS Total (z = -1.07). When the mean scores of the children in the control group were taken into consideration, there was an increase in the posttest scores. It is thought that this could be due to the result of the acquisition of cognitive and language development gains and indicators in Turkish Ministry of National Education Preschool Education Program (2013) applied to children and the normal course of improvement in children's academic and language skills during the research process.
Table 5 presents a significant difference in favor of the experimental group when the researchers sought for difference between the posttest scores of children in the study group in terms of the subtests of K-SEALS: Vocabulary (U=-2.442, p>0.05), Numbers, Letters and Words (U=-2.22, p>0.05) Articulation Survey (U=-2.42, p>0.05), K-SEALS Total (U=-2.878, p>0.05). It can be argued that Pattern-based Mathematics Education Program is effective on preschoolers’ early academic and language skills in the light of this result.
Early learning experiences play a critical role in children's lifelong learning (Clements and Sarama, 2011). Especially short and long-term effects are seen in cognitive and social development of children who are included in qualified education programs in early childhood (Jackman, 2012). The characteristics of pattern functions and algebra are a guiding task for teachers who want to develop preschool class activities that are fun, and children can participate tirelessly (Smith, 2009).
Children can develop critical thinking and problem-solving skills when working with pattern activities. At the same time, patterns and relationships are an important concept in understanding and generalizing mathematical thinking
and relationships, in developing reasoning skills (Papic and Mulligan, 2005), and in understanding the order and logic of mathematics (Burns, 2015). Patterns include counting and operation skills by their structure and children can use mathematical concepts and develop matching, sorting, grouping and comparison skills (Papic and Mulligan, 2005; Palabıyık and Akkuş-İspir, 2011). In this study, which investigates the effect of Pattern-based Mathematics Education Program on 61-72 month old children's early academic and language skills, a statistically significant difference (p <0.05) was found in favor of the experimental group. This was so when the researchers compared the posttest results of Kaufman Survey of Early Academic and Language Skills (Vocabulary, Numbers, Letters and Words, Articulation Survey and K-SEALS Total). Other independent variables, which were not observed and/or controlled by the researchers prior to the implementation, might have contributed slightly to this finding but this is the case for the quasi-experimental design (Cook and Campbell, 1979). In the case of the control group, there was no statistically significant difference (p>0.05) between the pretest and posttest scores of the Kaufman Survey of Early Academic and Language Skills (Vocabulary, Numbers, Letters and Words, Articulation Survey and K- SEALS total). In this study, which is limited to the number of children in the study group and activities in the Pattern-based Mathematics Education Program, it was found that the Pattern-based Mathematics Education Program was effective in supporting the early academic and language skills of 61-72-month-old preschoolers.
In Pattern-based Mathematics Education Program, there were efforts to provide enriched environments for children, to ensure active participation, to have activities to support all developmental domains, to create awareness about the concept of pattern, to associate mathematical concepts with daily life and to discover that mathematics is in every aspect of life. In the program, activities involving all sensory organs and the ability to find the logical relationship between words, classification of objects, concepts or events, cause-effect relation, the ability to see the relationship between words and sentences, and find the logical relationship between words, especially given the children in sound (music) patterns classifying the elements in the pattern. This established the cause-effect relationship and exploring the logical relationship in the elements of the pattern, making activities to generalize the pattern have an effect on the development of early academic and language skills of the children in the experimental group. At the same time, the integration of activities in the program with fields such as science, art, music and games and the inclusion of pattern forms for all sense organs can be considered as the reason for this result.
Parallel findings have been reported in the literature. For example, Gök-Çolak (2016) found that the Pattern-based Mathematics Education Program had a positive effect on verbal and numerical reasoning skills of 61-72-month-old children. Papic (2007) found that a six-month early intervention program focusing on repetitive, spatial patterns had an impact on children's early number skills. Mulligan et al. (2008a) found that the PASMAP (Pattern and Structure Mathematics Awareness Project) project, which was related to the concept of pattern and the place of pattern and algebra in mathematics programs, contributed positively to children's mathematical skills. Rittle-Johnson et al. (2016) pointed out that early repeating patterning activities predicted children’s mathematics knowledge and development. Recently, as an outcome of the longitudinal studies carried out by Nguyen et al. (2016) and Rittle-Johnson et al. (2017) it was stated that working with repeating patterns in early childhood predicted children’s mathematics achievement at fifth and sixth grades. Likewise, it has also been reported that awareness raising on patterns and relationships were positively correlated with mathematical achievement (Booth and Thomas, 2000; Mulligan and Mitchelmore, 2009), analogical reasoning (English, 2004), mathematical reasoning (Mulligan et al., 2008b; Papic, 2015; Warren and Cooper, 2008). In addition, it was found out that pattern awareness in children influenced the understanding of number concepts and processes such as counting, distribution and numbering (Mason et al., 2009; Thomas et al., 2002).
On the other hand, Kidd et al. (2013) carried out a research on a pattern-based education program for elementary school students and concluded that the subjects benefited highly from the education while Kidd et al. (2014) reported that patterning instruction had large, fully mediated effects on both reading and mathematics in their research on the first graders.
Considering the concept of pattern as a nested concept of music and using music patterns in mathematical pattern studies (Edelson and Johnson, 2003; Geist et al., 2012; Zentner and Eerola, 2010), it has been reported that it children’s vocabulary enhanced (Moyeda et al., 2006). In addition, developments were seen in language skills (Marin, 2009), phonological awareness, vocabulary, semantics, syntax and phonetics (Curtis, 2007) when children participated in activities including rhythm, songs and games. These studies are likely to support the idea that Pattern-based Mathematics Education Program affected children’s acquisition of skills related to vocabulary, articulation and phonology.
In the light of the conclusions we draw from our findings, the following implications may be presented:
(i) Policy makers, teacher training institutions, researchers, preschool teachers and parents should work together to understand the importance of early academic and language skills in preschool period. In this regard, policy makers and universities can support projects aimed at increasing children's relevant knowledge and skills.
(ii) Pattern-based Mathematics Education Program can be integrated into Turkish Ministry of National Education Program in accordance with all age groups.
(iii) In line with the principles and characteristics of the Pattern-based Mathematics Education Program, interdisciplinary studies can be conducted based on holistic development.
The authors have not declared any conflict of interests.
REFERENCES
|
Balfanz R, Ginsburg HP, Greenes C (2003). The big math for little kids early childhood mathematics program. Teaching Children Mathematics 9(5):264-268.
|
|
|
|
Billstein R, Libeskind S, Lott J, Boschmans B (2016). A problem solving approach to mathematics for elementary school teachers (12th edition). USA: Pearson.
|
|
|
|
|
Birken M, Coon AC (2008). Discovering patterns in mathematics and poetry. Amsterdam: Rodopi.
|
|
|
|
|
Booth RDL, Thomas MOJ (2000). Visualization in mathematics learning: arithmetic problem-solving and student difficulties. Journal of Mathematical Behavior 18(2):169-190.
Crossref
|
|
|
|
|
Burns M (2015). About teaching mathematics. A-K 8 research. (4nd ed). Sausalito, California: Math Solutions.
|
|
|
|
|
Büyüköztürk Åž, Kılıç-Çakmak E, Akgün ÖE, Karadeniz Åž, Demirel F (2011). Bilimsel araÅŸtırma yöntemleri. Ankara: Pegem Akademi.
|
|
|
|
|
Carpenter TP, Franke ML, Levi L (2003). Thinking mathematically: Integrating arithmetic and algebra in elementary school. England: Heinemann.
|
|
|
|
|
Charlesworth R, Lind KK (2007). Math and science for young children. (Fifth edition). USA: Thomson Delmar Learning.
|
|
|
|
|
Clements DH, Sarama J (2007). Building Blocks-SRA Real Math Teacher's Edition, Grade PreK. Columbus, OH: SRA/McGraw-Hill.
|
|
|
|
|
Clements DH, Sarama J (2011). Early childhood mathematics intervention. Science 333(6045):968-970.
Crossref
|
|
|
|
|
Diezmann CM, Watters JM, English LD (2001). Difficulties confronting young children undertaking investigations In M van den Heuvel-Panhuizen (Ed ), Proceedings of the 25th annual conference of the International Group for the Psychology of Mathematics Utrecht, The Netherlands: PME Education pp. 353-360.
|
|
|
|
|
Edelson RJ, Johnson G (2003). Music makes math meaningful. Childhood Education 80(2):65–70.
Crossref
|
|
|
|
|
English LD (2004). Promoting the development of young children's mathematical and analogical reasoning. In English LD (2004), Mathematical and analogical reasoning of young learners Mahwah, NJ: Lawrence Erlbaum pp.201-214.
Crossref
|
|
|
|
|
Etopio EA (2009). Characteristics of early musical environments associated with preschool children's music skills. Doctoral's Thesis, The State University of New York, UMI Number, 3342135.
|
|
|
|
|
Gay LR, Mills GE, Airasian P (2005). Educational research: Competencies for analysis and applications (8th ed.). Upper Saddle River, NJ: Pearson.
|
|
|
|
|
Geist K, Geist EA, Kuznik K (2012). The patterns of music young children learning mathematics through beat, rhythm, and melody, Young Children (5)2:74-79.
|
|
|
|
|
Gök-Çolak F (2016). Örüntü temelli matematik eÄŸitimi programı'nın 61-72 aylık çocukların akıl yürütme becerisine etkisi. Yayınlanmamış Yüksek Lisans Tezi, Gazi Üniversitesi, EÄŸitim Bilimleri Enstitüsü, Ankara.
|
|
|
|
|
Griffin S (2004). Teaching number sense. Educational Leadership, 61(5):39-42.
|
|
|
|
|
Heppner PP, Wampold BE Kivlighan DM (2008). Research design in counseling (3. edition). USA: Thomson, Belmont. C.A.
|
|
|
|
|
Hargreaves M, Shorrocks Taylor D, Threlfall J (1998). Children's strategies with number patterns. Educational Studies 24(3):315-331.
Crossref
|
|
|
|
|
Jackman HL (2012). Early education curriculum a child's connection to the world. (Fifth edition). USA: Wadsworth, Cengage Learning.
|
|
|
|
|
Kaufman AS, Kaufman NL (1993). K-SEALS Kaufman survey of early academic and language skills: Manual. Minneapolis: Pearson Assessments.
|
|
|
|
|
KesicioÄŸlu OS (2013). Okul öncesi dönem çocuklarının matematiksel örüntü becerilerinin incelenmesi. Akdeniz EÄŸitim AraÅŸtırmaları Dergisi 7(13):19-26.
|
|
|
|
|
Kidd JK, Carlson AG, Gadzichowski KM, Boyer CE, Gallington DA, Pasnak R (2013). Effects of patterning instruction on the academic achievement of 1st-grade children. Journal of Research in Childhood Education 27:224-238.
Crossref
|
|
|
|
|
Kidd JK, Pasnak R. Gadzichowski KM, Gallington DA, McKnight P, Boyer CE (2014). Instructing first-grade children on patterning improves reading and mathematics. Early Education and Development 25:134-151.
Crossref
|
|
|
|
|
Lan-Ma H (2007). The potential of patterning activities to generalization. In Woo JH Lew HC, Park KS, ve Seo DY (Ed.), Proceeding of The 31st Conference of the international Group for the Psychology of Mathematics Education Seoul:PME. 3:225-232.
|
|
|
|
|
Marin MM (2009) .Effects of Early Musical Training on Musical and Linguistic Syntactic Abilities [abstract]. New York Academy of Sciences 1169(1):187-190.
|
|
|
|
|
Mason J, Stephens M, Watson A (2009). Appreciating mathematical structure for all. Mathematics Education Research Journal 21(2):10-32.
|
|
|
|
|
Milli EÄŸitim Bakanlığı [MEB] (2013). Okul Öncesi EÄŸitim Programı.
|
|
|
|
|
Moyeda IXG, Gómez IC, Flores MTP (2006) .Implementing a Musical Program to Promote Preschool Children's Vocabulary Development. Early Chılhood Research and Practice, 8(1). Çevrim içi:
|
|
|
|
|
Mulligan J, Mitchelmore MC (2009). Awareness of pattern and structure in early mathematical development. Mathematics Education Research Journal 21(2):33-49.
|
|
|
|
|
Mulligan JT, Mitchelmore MC (2013). Early Awareness of Mathematical Pattern and Structure. In: English L, Mulligan J (eds) Reconceptualizing Early Mathematics Learning. Advances in Mathematics Education. Springer, Dordrecht.
|
|
|
|
|
Mulligan J, Mitchelmore M, Kemp C, Marston J, Highfield K (2008b). Encouraging mathematical thinking through pattern and structure: an ıntervention in the first year of schooling. Australian Primary Mathematics Classroom, (AMPC), 13(3):10-15.
|
|
|
|
|
Mulligan J, Mitchelmore M, Marston J, Highfield K, Kemp C (2008a). Promoting mathematical pattern and structure in the first year of schooling: An intervention study. In O. Figueras, J. Cortina, S. Alatorre T, Rojano A. Sepúlveda (Eds.), Proceedings of the Joint Meeting of PME 32 and PME-NA, México: Cinvestav-UMSNH. 30(4):1-8).
|
|
|
|
|
National Council of Teachers of Mathematics (NCTM) (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
|
|
|
|
|
Neuman SB, Dickinson DK (2002). Handbook of early literacy development. Newyork: Guilford Publication.
|
|
|
|
|
Nguyen T, Watts TW, Duncan GJ, Clements DH, Sarama JS, Wolfe C (2016) .Which preschool mathematics competencies are most predictive of fifth grade achievement? Early Childhood Research Quarterly 36:550-560.
Crossref
|
|
|
|
|
Olkun S, Yeşildere S (2007). Sınıf öğretmeni adayları için temel matematik 1.Ankara: Maya Akademi.
|
|
|
|
|
Palabıyık U, Akkuş-İspir O (2011). Örüntü temelli cebir öğretiminin öğrencilerin cebirsel düşünme becerileri ve matematiğe karşı tutumlarına etkisi. Pamukkale Üniversitesi Eğitim Fakültesi Dergisi 30(11):111-123.
|
|
|
|
|
Papic M (2007). Promoting repeating patterns with young children--more than just alternating colours. Australian Primary Mathematics Classroom [APMC] 12(3):8–13.
|
|
|
|
|
Papic M (2015). An early mathematical patterning assessment: identifying young Australian Indigenous children's patterning skills. Mathematics Education Research Journal 27(4):519 534.
Crossref
|
|
|
|
|
Papic M, Mulligan JT (2005). Pre-schoolers' mathematical patterning. In P. Clarkson, A. Downton, D. Gronn, A. McDonough, R. Pierce, and A. Roche (Eds.), Building connections: Theory, research and practice (Proceedings of the 28th annual conference of the Mathematics Education Research Group of Australasia, Melbourne, Sydney: MERGA. pp. 609-616.
|
|
|
|
|
Papic MM, Mulligan JT, Mitchelmore MC (2011). Assessing the development of preschoolers' mathematical patterning. Journal for Research in Mathematics Education 42(3):237-269.
|
|
|
|
|
Rittle-Johnson B, Fyfe ER, Hofer KG, Farran DC (2017). Early math trajectories: Low-income children's mathematics knowledge from ages 4–11. Child Development 88(5):1727-1742.
Crossref
|
|
|
|
|
Rittle-Johnson B, Zippert EL, Boice KL (2016). The roles of patterning and spatial skills in early mathematics development. Early Childhood Research Quarterly 20:196-199.
Crossref
|
|
|
|
|
Sarama J, Clements DH (2009). Early childhood mathematics education research: Learning trajectories for young children. Newyork: Routledge.
|
|
|
|
|
Thomas N, Mulligan JT, Goldin GA (2002). Children's representations and cognitive structural development of the counting sequence 1-100. Journal of Mathematical Behavior 21:117-133.
|
|
|
|
|
Uyanık Ö, Kandır A (2014). Kaufman Erken Akademik ve Dil Becerileri AraÅŸtırma Testi'nin 61-72 aylık Türk çocuklarına uyarlanması. Kuram ve Uygulamada EÄŸitim Bilimleri 14(2):669-692.
Crossref
|
|
|
|
|
Warren E (2005). Young children's ability to generalise the pattern rule for growing patterns. In H. Chick and J. Vincent (Eds.). Proceedings of the 29th conference of the International Groupfor the, Melbourne: Program Committee, Psychology of Mathematics Education 4:305-312.
|
|
|
|
|
Warren E, Cooper T (2006). Using repeating patterns to explore functional thinking. APMC 11(1):9-14.
|
|
|
|
|
Warren E, Cooper T (2008). Patterns that support early algebraic thinking in the elementary school. In C. Greenes and R. Rubenstein (Eds.) Algebra and algebraic thinking in school mathematics: Seventieth Yearbook, Reston, VA: National Council of Teachers of Mathematics pp.113-126.
|
|
|
|
|
Waters J (2004). Mathematical Patterning In Early Childhood Settings, Mathematics Education for the 3rd Millennium: Towards 2010 (Proceedings of the 27th Annual Conference of the Mathematics Education Research Group of Australasia), Editors: In I. Putt, R. Faragher ve M. McLean, MERGA pp. 565-572.
|
|
|
|
|
Zentner M, Eerola T (2010). Rhythmic engagement with music in infancy. Proceedings of the National Academy of Sciences (PNAS) 107(13):5768–5773.
Crossref
|
|