In order to facilitate prospective teachers’ understanding of their classes, they can be imbued with declarative knowledge and professional vision. Improving professional vision is strongly related to the knowledge-guided process (Stürmer et al., 2013). This vision can be developed by transforming procedural knowledge, which is a semiotic model, into declarative knowledge, which is the knowledge of how to do a procedure within the  scope of certain and clear rules (Georgeff and Lansky, 1986; Georgeff et al., 1985; Özenli, 1999, p. B2). In relation to a given piece of perceived information, a semantic coordination is made that resolves the meaning of the information by partition of the procedural knowledge, into sublevels, as follows. Even though it is stated in the literature that knowledge transitions support learning, it is emphasized that this  transition is mostly from declarative knowledge to declarative knowledge or from declarative knowledge to procedural knowledge (Anderson, 1983, 1993; Harvey and Anderson, 1996; Singley and Anderson, 1985, 1989).

Models and modeling

Models and modeling are widely used in science and science education to ease learning. Models are scrutinized according to meaning, purpose, multiplicity, change, and uses in the science classroom. Models developed with attention to each of these areas should be used by science teachers and their use promoted (Oh & and Oh, 2011). However, some science teachers, despite being able to clearly sum up the features of particular models, may not focus properly on using and understanding them (e.g., Lin, 2014).

Semiotics

The usage of such semiotic features ensures the understanding of different information structures (May & and Dhillon, 2009). Knowledge can be defined in semiotic terms, and for knowledge transitions between procedural and declarative knowledge, semiotic models can be used. When these models are constructed in a way that is appropriate for the students’ academic objectives, they might affect reconstruction of knowledge and hence achievement in learning (Tochon, 1998). Problem solving conducted by university students can be defined by semiotic models. In addition, the semiotic errors that the students commit when engaged in problem solving involving complex operations and complex concepts can easily be defined (Godino, et al., 2005).

Semantic network

To construct a semantic network, one must first unitize knowledge into its smallest subunits (in physics problems, this usually requires unitizing into symbols) and create phases among these smallest subunits by relating them to their meanings. The network in which synthesis of knowledge (that is, the solution to the problem) is conveyed using signs relating these phases to their meanings is called a semantic network. As this pictorial network shows the content and relations between elements of the content of the knowledge, as well as the order in which these relations should be made, it can facilitate students’ reconstruction of the knowledge.

A semantic network showing the construction of knowledge conducted by reconstructing two pieces of procedural knowledge can be exemplified by  a  problem-solving process on a particular topic, in this case one related to the subject of magnetism. For instance, there is a +q charged particle that enters a magnetic field at speed v. We want to find the acceleration of this particle in the magnetic field? If a (acceleration) can be concluded with 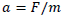. However, a direct calculation is impossible with this formula, because the F magnetic force, which has an effect on a proton in the magnetic field, is not given. Yet, the F force, which affects a particle that is entering the magnetic field, can be concluded with 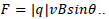These correlations are an instance of declarative knowledge constructed from two pieces of procedural knowledge, and in this case new calculation procedures are needed. For declarative knowledge, this calculation process is as follows: multiply q, v, and B, record the result, calculate the sin of angleθ (sinθ)and record the result, and multiply these two recorded results and record the result. Divide the result by m_p and record the result. This calculation sequence is declarative knowledge and can be shown by a semantic network, given for this case in Figure 1. Figure 1 will be called Pictorial Diagram 1.

 

 

Semiotic declarative knowledge model

Figure Pictorial Diagram 1 is a semantic network that does exemplify the declarative knowledge model of a charged particle entering a magnetic field. For declarative knowledge in this diagram, two pieces of procedural knowledge have been use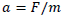d:  and 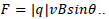Pictorial representations of these two pieces of procedural knowledge are given in Figure 2(2a and 2b). Figure 2 will be called Pictorial Diagram 2; t These diagrams show semantic networks that exemplify how the transition from procedural knowledge to declarative knowledge can be achieved. The calculation sequences and diagrams given constitute a knowledge model that phases the subunits of the declaration and shows how semantic coordination among these subunits can be done (the arrows in the diagram).

 

 

The big circles acceleration in the semantic network in Figure Pictorial Diagram 1, where the main elements of acceleration are placed, will be called knots. The stimulation of the knot indicates that the related calculation (or procedure) is completed. The black dots around the big circles will be called synapses; these are the stimulants that ensure the link between the knots that they belong to and other knots. Stimulating the synapses means the related calculation (or procedure) begins. Synapses can be present in two statuses: stimulated and non-stimulated. If a synapse is stimulated, then the knot that it is linked to is stimulated as well and the stimulation that comes out of the knot is transferred through all available pathways as far as the last synapses. A synapse is stimulated only if all arrows that are directed toward it are    themselves    stimulated.   This    makes     up    the semantic network in its totality. As there are no synapses on the knots, the knots need to be stimulated extrinsically. This stimulation is effected by data or information, and in turn allows the stimulation of the whole network. For the network shown in Figurepictorial diagram 1 to be stimulated, some of the knots should be stimulated extrinsically. Extrinsic stimulation of a knot is possible by giving it extrinsic data. When this is possible, the stimulated status will spread extensionally through the knots of the network and this process will become stable, leaving the network statically stimulated. In the diagram, synapses are shown with reference numbers 1, 2, 3, 4, and 5, and procedures are shown  with  reference numbers 1, 2, and 3 in parentheses in the knots. It is clear that the solution of a problem starts with particular data. In this study, the data for the example are . These data and their links are shown in Pictorial Diagram 1. Starting with synapse 1 in the diagram means starting the related procedure (the 1st procedure) for sin calculation. For synapse 1 to be stimulated, knot θneeds to be stimulated; in this case, knot θ is stimulated extrinsically by the entrance of data for θ. Therefore, the extrinsically stimulated knot θ stimulates synapse 1. Stimulation of synapse 1 starts the 1st procedure for sin calculation, that is, for the sin value of θ, and therefore stimulates    the    “sin”    knot,   meaning    that    the   sin calculation is complete. When the “sin” knot is stimulated, synapse 2 is stimulated. If synapse 3 is stimulated along with synapse 2, the 2nd procedure begins and the F knot is also stimulated. The 2nd procedure is multiplying synapses 2 and 3. Synapse 3 is stimulated by giving q, v, and B data extrinsically. That is, as q, v, and B data are extrinsically stimulated, synapse 3 is stimulated. Stimulation of synapses 2 and 3 means that the required procedure (the 2^nd procedure) begins to calculate the given force by 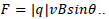.Transition of the F knot into a stimulated form means that the calculation of F using necessary procedural information is complete. As the F knot is stimulated, synapse 4 is also stimulated. If synapse 5 is stimulated along with synapse 4, the 3rd procedure begins, and the “a” knot is stimulated in turn. The 3rd procedure is multiplying synapses 4 and 5. Synapse 5 is stimulated by giving〖 m〗_p data intrinsically. That is, as knot m_p is extrinsically stimulated by the data, synapse 5 is stimulated. Stimulation of synapses 4 and 5 means that the required procedure (the 3^rd procedure) begins to calculate given acceleration by 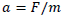.. Transition of the “a” knot into a stimulated form means that the calculation using necessary procedural information is complete. This model based on semiotic systems is called a semiotic model. Therefore, as the network transits into a stable form, “declarative knowledge” is defined using necessary data or information. This declarative knowledge is defined by a problem-solving technique. In this case (in the solution of a problem) the semiotic model constructed by using procedural information is a semiotic declarative model. This model can be constructed in order to ease the understanding of declarative knowledge of all magnetism.

Problem-solving techniques

It has been shown in education research that it is significantly effective for students to use problem-solving techniques to solve mathematics and physics problems (e.g., Heckler, 2010). Students’ use of problem-solving techniques might allow them to both construct and develop problem-solving procedures and knowledge (Dijkstra, 1997). However, it is discussed in the literature whether with the help of problem-solving stages, the organization of system features and control and communication procedures might be shown. Control in the problem-solving stages is three-dimensional: the first dimension is cooperation among units, the second is the organization of units, and the third represents the action of reaching a solution by constructing the correct or needed form of cooperation (e.g., Decker, 1987).

Drawing diagrams (free-body diagrams) help students in physics problem solving. These diagrams drawn step by step are included among general problem-solving techniques (Heckler, 2010). In physics classes, a problem can be solved by dividing into a) given-asked b) free-body diagram c) theory d)  formula,  and  e)  calculations  units.

These units are also defined as the variables of the problem (Yılmaz & and Yalçın, 2012a, 2012b, 2012c, 2012d).

Learning systems

Though many studies investigate the acceleration of learning in humans and machines, it has been claimed that it is not possible to make a general learning theory constituted by more complex algorithms combining aspects of all fields (human, machine, etc.). On the other hand, it has also been claimed that a “mathematical universal learning system theory of algorithms and computable functions might be developed; such a “universal learning system” would be capable of learning to control in an optimal way any given constructive system from a given class or theoretical context (Shimansky, 2004).

The first adaptive learning research was focused on facilitating a single individual knowledge source, such as students’ learning styles, cognitive styles, or achievement of learning, following adaptive learning approaches focused on facilitating “two main sources of personalized knowledge,” such as students’ learning behaviors and individual learning styles. The new adaptive learning approaches used in these studies proved that individual learning efficiency and learning achievement can be facilitated thereby (e.g., Tseng  et al., 2008).

Özenli (1999, pp. C1–C2) defines adaptive learning systems within a cybernetic frame as systems which have the ability to improve and reform their functional structure and features when there is little previous information about the operational circumstances and educational needs caused by operational obligations. Learning systems depend on learning processes within their own operations. These processes help learning systems gain information and address its lack. Any learning should have an objective, which should implicitly include developing knowledge required for learning and facilitating the operation of learning processes. If we use a particular performance index to assess learning optimality, the learning objective will be limited by optimality criteria, helping create optimal operational circumstances. This objective can be achieved by changing the structure of learning processes depending on data processing and operational circumstances—changing related parameters into a system. One of the characteristics such of a learning system is learning speed.

The teacher’s (educator’s) role is not only transferring formal information, but also, explaining the aim of learning and developing positive and constructive behavior models for learners (learning systems), such as a semiotic procedural and declarative knowledge model. These semiotic models can be developed using the components of control mechanism, evaluation mechanism, and objective-aimed systems (Özenli, 1999, p. C2). A general learning theory able to achieve the two different objectives of education and teaching can be modeled by these systems and mechanisms using the semiotic declarative knowledge model. A general mathematical theory of learning systems can be defined in terms of a universal learning system and a constructive system. These definitions are based on a constructive optimal control idea and shown by particular algorithms (e.g., Shimansky, 2004). This study focuses on defining the variables that affect problem solving as a mechanism. The definitions that will be used, based on the working mechanism of an adaptive learning system that affects the variables of problem solving, are given as follows in Özenli (1999): a learning system works with 1) an evaluation mechanism and 2) a control mechanism. The evaluation mechanism is necessary for a system (individual) to decide whether to change actions (intellectual) to gain the optimal benefit. For an individual to move as part of this mechanism, s/he must have the perception ability of his/her own intended-for-purpose performance, directly or indirectly…. For an individual, there are many definitions of “purpose”: In this study, we define a “purpose” as a main quality that an individual desires or wants to reach at a given epistemological level and under valid circumstances. Therefore, an individual has or should have different objectives at different epistemological levels or could be considered based on different objectives….

…objective-aimed systems are 1) enactor systems. In this study, the objective is to maximize a certain “utility function” of an individual defined by output conditions. 2)

Self-organized systems. Performance is stated as sort of measurement of organization (such as Shannon entropy measurement). 3) Mistake-tolerant systems. In spite of performance failure of system components based on reliability measurement or false warnings, the objective generates correct reactions (answers).

…a control mechanism, on the other hand, based on performance information by an evaluation mechanism is responsible for making a necessary change or changes in the actions or determining the final action. This control mechanism has three components (features). 1) Entropy reduction. In order to adapt a particular environment or circumstance reducing the alternatives of actions and behaviors again and again (one after another). 2) Preserving variations. Preserving the alternative (or alternatives) that is not yet to be desired but will be beneficial in the future. 3) Selective omission. Omitting the alternatives that were once well accepted for an environment but are not related or suitable now (pp. C1-M11).

Data processing of an objective-aimed learning system depends on the right decisions regarding evaluation and control mechanisms. The decisions to be made are defined Özenli (1999):

…For objective-aimed individuals “decision making”  is  of high importance. Decision is the process of searching for an exit in an “unspecific environment” and choosing between a minimum two data or between two subunits of a single data in order to move forward. This process depends on the ability of the decision maker, the problem that requires decision, and its evaluation. Therefore, decision is choosing one of two or more options. The individual first determines the situation, presents many options, evaluates these options, and finally chooses one of them, and that he is free in his choice.

The most important point in decision making is the relation between option generation and evaluation processes, and based on these, five types of “decisions” occur: 1) Impulsive, here, evaluation of the option ceases. 2) Risky, the option is only partially evaluated. 3) Balanced, option generation and evaluation are well balanced. 4) Precautious, evaluation partially suppresses option generation. 5) Inert, option generation is fully suppressed and the circumstance is completely ambiguous….(pp. C1-M11).

Education can be considered as a body of systems. The research conducted by Özenli (1999) can be explored in order to explain the relations between education systems included in this section. In this study, along with these definitions made for the learning system, a particular area of general learning theory based on problem solving will be modeled.

Aim

Education can be addressed as a body of systems. This study aims to develop a semiotic declarative knowledge model which is to combine systems available in order to help improve the understanding of science teacher candidates.  This model can be developed theoretically and experimentally using problem solving techniques. A model will be developed to make an active professional contribution to the learning needs of prospective science teachers by easing their understanding and helping them to think accurately and ask the right questions. To help prospective teachers develop and facilitate their functional structure and features and raise the available information to a desired level, optimality criteria will be used. In order to acquire an optimal knowledge level based on these criteria and operating conditions, a semiotic declarative knowledge model will be developed through problem-solving techniques.

In this research, a semiotic declarative knowledge model will be theoretically and experimentally developed through the variables used in problem solving. As the semiotic model will be developed through a declarative problem-solving technique, it will be called a semiotic declarative knowledge model. This model will be developed by extending a sample  semiotic  model  developed to solve a given problem, so as to solve many problems. Instead of using a knot, as in the pictorial diagrams, independent variables related to problem-solving techniques will be used. There will be two main independent variable groups in this study: knowledge-level variables (KLV) and procedural variables (PV).

This research is a case study in which data was collected in the week following the expression of magnetism. Statistics were calculated with the probability and possibility calculation statistics for data variables (VDOÄ°HÄ°) (Yılmaz, 2011; Yılmaz & and Yalçın, 2011) using packaged software developed for use with this statistical technique. The data were collected using four measurement tools, from 35 prospective science teachers of 1st-graders. These four measurement tools were “measurement tool 1” (MT1); a) the problems used in MT1 were given, b) “measurement tool 2” (MT2), which assessed whether the formulas were known, c) “measurement tool 3” (MT3), which assessed whether the mathematical calculations were known and d) “measurement tool 4” (MT4), which assessed the scientific knowledge. The data were collected through measurement tools MT2, MT3, MT4 and MT1, in that order. As MT2, MT3, and MT4 constituted procedural knowledge needed for MT1, they will be called the independent procedural variables (PVs) of the study. Given-asked, free-body diagram (FBD), formula, and operation units used in the solutions to problems given in MT1 will be called independent knowledge-level variables (KLVs). In practice, prospective teachers were expected to solve MT1 using KLV steps. Therefore, the study has three independent PVs and four independent KLVs, seven variables in all, in which the participants’ knowledge level will be calculated. Achievement level assessed by MT1 the only dependent variable in this study is ASS.

The probability and possibility calculation statistics for data variables (VDOÄ°HÄ°) technique and its relevance to the research

Scoring of the variables and calculations on the scores are done using the VDOÄ°HÄ° combined stage statistical technique developed by Yılmaz (2011). This technique involves segmenting the variables into their “smallest significant pieces” (AKPs) and conducting statistical calculations by scoring these AKPs. In this statistical technique, first it is determined how many smallest significant pieces each variable of a problem consists of its ordinary score; then it is determined how many of these smallest significant pieces are included in the collected experimental data (the existing score); finally, dividing the existing score by the ordinary score gives the statistical results. In their studies, Yılmaz (2011) and Yılmaz & and Yalçın (2011) state that in experimental data, the smallest significant pieces can be given to the scores of -1, 0, and 1 scores. These scores can be given to both independent and dependent variables; in this study, independent and dependent variables will be scored separately and a statistical correlation between them will be made. The dependent variable will be correlated with four KLVs and three PVs in five different stages, based on the positive or negative values of the scores.

The proportional results obtained from the calculations will be called level results. Levels will be calculated for independent and dependent variables, and the percentages of these levels will be used in the independent–dependent and independent–independent variable correlation analyses. Knowledge and achievement levels can be determined objectively through packaged software program developed for the probability and possibility calculation statistics for data variables(VDOÄ°HÄ°) combined stage statistical technique (Yılmaz, 2011, 2012, 2014).

Statistical method

Measurement tools  MT2,  MT3,  and  MT4  were  designed  only  to determine independent PV variables. MT1, on the other hand, was designed to determine both independent KLV and a dependent variable (ASS), and the data were collected all in the same session. These measurement tools include open-ended questions that can define prospective teachers’ declarative knowledge and achievement levels and can correlate these knowledge rates with achievement levels. Moreover, the questions asked by these measurement tools were prepared in order to develop prospective teachers’ semiotic declarative knowledge models.

MT1 consists of seven open-ended questions that aim to calculate independent KLV and dependent variable ASS. Among these questions, there are those that do not require FBD drawing and FBD knowledge level—these are calculated independent from these two questions. The other independent KLV knowledge levels of this measurement tool were calculated under the assumption of seven questions. The questions yielded by this measurement tool are declarative knowledge questions taken from magnetism topics in general physics 2 for prospective science teachers of 1st-graders

MT2, MT3, and MT4 were prepared suitable to determine the procedures needed for prospective teachers to solve MT1. Among these measurement tools, the formula KLV variable of MT2 and MT1, the operation KLV variable of MT3 and MT1, and all KLV variables of MT4 and MT1 can be correlated. As these three PV measurement tools include procedures required to solve MT1, therefore, they must have been applied before MT1. The questions on PV measurement tools are correlated with more than one question from MT1.

MT2 will be called the Formula (PV) variable. It consisted of 36 formulas required to solve questions on MT1. In MT2, formulas related to MT1 were given and participants were asked to write the name of the formula and a related topic. For the MT1 formula (KLV) variable, the question asked participants to write the formulas used in the solution (that is, a correlation between the knowledge level of these two measurement tools was assured).

MT3 will be called Basic Mathematics (PV). It consisted of 50 mathematical questions required to solve the questions on MT1. In this measurement tool, basic mathematical knowledge was investigated and then used in the MT1 operation (KLV) variable. Therefore, a direct correlation between MT3 and the MT1 operation (KLV) variable was assured.

MT4 will be called Scientific Knowledge (PV). It consisted of 13 questions determining scientific knowledge procedures required to solve the questions on MT1. Six of these questions were procedural knowledge questions and seven were mathematical logic questions, and prospective teachers’ level of knowledge on these questions can be correlated with knowledge and achievement level for all variables in MT1.

Semiotic method

Depending on the task, assessment mechanism variables will be defined as given-asked (KLV), FBD (KLV), formula (PV), basic mathematics (PV), or scientific knowledge (PV). Formula (KLV) and operation (KLV) variables will be defined as the control mechanism. These variables (KLV and PV) will be shown as knots in the semiotic model. The stimulants that assure connection among knots will be called synapses. Synapses will be numbered depending on the knot that they belong to. The first knot is the given-asked knot, where assessments of information/data are made and separated. The second one is the scientific knowledge knot, where assessments are made to define regularities and cognitive models that seem relatively independent from one another. The stimulant that keeps the connection between the given-asked knot and the scientific knowledge knot will be called synapse 1. The following knot is the formula (PV) knot, where assessments to define physical regularities are made; the stimulant that assures the connection between this knot and the  scientific  knowledge  knot  is synapse 2.

The next knot is the basic mathematics knot, where assessments to define mathematical regularities are made; the connection between this knot and the scientific knowledge knot is synapse 3. The next knot is the FBD knot, where problem-specific formulas are developed for the problems that will lead to the result. As cognitive modules in the data flow are defined in this knot, it constitutes an assessment mechanism. The connection between this knot and the formula knot (PV) is assured by synapse 4, that to the scientific knowledge knot by synapse 5 and that to the basic mathematic knot by synapse 6. The following knot is the formula (KLV) knot, where the first control is done. In this knot, the necessary changes are made to formulas received from the formula (PV) knot or the FBD knot, and the final formula is determined. The connection between formula (KLV) and formula (PV) is assured by  synapse  7  and  that with the FBD knot by synapse 8. The final knot is the operation knot, where the second control is done and the result/output is determined. In this knot, along with the stimulants sent from other knots, a final action (result, ASS) is determined. The connection between this knot and the given-asked knot is assured by synapse 9, that to the formula (KLV) knot by synapse 10, and that to the basic mathematic knot by synapse 11. When synapses reaching the operation knot are stimulated, the data received from the related knots are used to determine the final action. A semantic network of declarative knowledge constituted using problem-solving techniques is given in Figure 3. Figure 3 will be called Pictorial Diagram 3. In this diagram, stimulation of the knots shown as variables means that the related operation is complete, while stimulation  of   the  synapses  that  ensure  the  connection  among knots means that the operation starts in the knots that they are linked to. According to this diagram, stimulant data entering (external stimulation) “given-asked” should stimulate synapse 1. This stimulation means that the related procedure begins in order to determine the scientific knowledge that the data belongs to. Stimulation of the knot labeled “Scientific Knowledge” means that the scientific knowledge this data belongs to is determined. 

 

 

A stimulated scientific knowledge knot in turn stimulates synapse 2; this stimulation means that the procedure begins that will determine formulas related to scientific knowledge. A stimulated synapse 2 stimulates the formula knot (PV), meaning that formulas related to problem solving are or are not determined. If the formula related to the solution of the problem is determined, synapse 7 is stimulated. This stimulation means that as the related procedure begins that will control the measurement of the formulas to be used in problem solving. A stimulated synapse 7 stimulates the formula knowledge (KLV) knot, meaning the measurement of the formulas is complete and the related formula is determined. A stimulated formula (KLV) knot stimulates synapse 10. This stimulation means that procedures related to problem solving begin, and in turn 10 stimulates the “operation” knot, meaning all related calculations are now complete. A stimulated operation knot stimulates synapse 12, beginning the procedure to choose the result in the operation knot and ultimately meaning the result is determined and becomes stable. If the formulas for the solution of the problem are not determined in the formula knowledge (PV) knot, synapse 4 is stimulated in order to determine a formula for the solution of problem, potentially along with synapses 3, 4, 5, and 6, which would lead to the inception of procedures related to image drawing to determine related formulas. In this case, the knot called FBD is stimulated, meaning FBD the related formula is determined by completing free body diagram operations. A stimulated FBD knot stimulates synapse 8, which means synapse 7 is also stimulated. The result is then determined using similar procedures. This model, based on semiotic systems, is called a semiotic model. Stabilization of the defined semantic network means that the required information is used and declarative knowledge is defined. The semiotic model used in the present study is a semiotic declarative knowledge model related to problem solving on magnetism topics.

The experimental model is developed according to the theoretical model with interactions between stimulants and stimulated by knowledge level, as acquired from the data collected by the measurement tools. The experimental model will be developed using the synaptic connections in the theoretical model. For the development of the experimental model, components of the control mechanism and the objective-aimed system will be analyzed; in this analysis, knowledge and achievement levels will be used.

Data were collected using a case study in order to experimentally improve the semiotic declarative knowledge model developed modeling the systems available in the theory section using problem solving techniques. Findings obtained from the data using the probability and possibility calculation statistics for data variables (VDOÄ°HÄ°) method will be interpreted statistically and semiotically, on an individual basis. First, findings will be interpreted statistically. Then, an experimental model will be developed using the interpretations obtained from these findings.

Statistical findings and Interpretations

Values acquired from scoring and analysis using the probability and possibility calculation statistics for data variables (VDOÄ°HÄ°) combined statistical method data, collected from 35 prospective science teachers of 1st-grade students using four measurement tools, as represented in Table 1. Findings for independent KLVs of MT1—Ä°S, APS, ANS, NAPS, and SS—are also given in the table, and the last column gives the sum of KLV values. The findings obtained from other measurement tools are given below the SS column. The last line gives the ASS value, which shows achievement level.

It is the given-asked variables that are the first KLV to affect the achievement level and divide some portion of the data into its subunits, and wherewith procedural (form) knowledge is transformed into declarative (structure) knowledge by choosing the correct option and making the right decision according to the objective-aims of these subunits. The knowledge level of this variable is given in the second column of Table 1. One of the most important features of this variable is that it is the one where question solving begins. Its importance for declarative knowledge specifically is that it determines the procedural  knowledge  used  in question solving and that it is the independent KLV that decides in which order procedures take place. It is thought that the possibility of the calculations done for this variable to affect the achievement level: positive stage values (APS) positively affect the achievement level (ASS) at the rate of 2%. Unrelated stage knowledge (Ä°S), negative knowledge (ANS), and positive knowledge in negative stages (NAPS) do not affect achievement level (0%). For the given-asked variable, zero score (SS), which shows the level of unknown knowledge, negatively affects the achievement level by as much as the sum of Ä°S, ANS, and SS, that is, 98%. For this independent KLV, the possibility of affecting achievement level in a positive way may only be as much as the sum of the APS and NAPS values, that is, 2%.

 

 

The second of the independent KLVs that affects achievement level is the free body diagram (FBD) variable. Calculations for this variable are given in the third column of Table1. Correlating this variable with the given-asked variable facilitates the creation of correct formulas related to the solution to the question. This is important for declarative knowledge because FBD is a KLV where some rules of the procedures are determined by figures. Positive stage knowledge for this variable is thought to positively affect achievement level by 16%, while unrelated stage knowledge affects the achievement level negatively by 1% and negative stage knowledge affects the achievement level negatively by 2%. Positive knowledge of negative stages might affect (NAPS) the achievement level positively by 1%. For this variable, zero score (SS), which shows the level of unknown knowledge, affects the achievement level negatively by 80%. This variable could affect the achievement level positively by a maximum of 17% and negatively (Ä°S, ANS, and SS) by a maximum of 83%.

The third independent KLV that affects the achievement level is the formula variable. Calculations for this variable are given in the fourth column of Table1. This variable is where basic procedures for the solution of the question are determined. Positive stage knowledge for this variable is thought to affect the achievement level positively by 20%, unrelated stage knowledge negatively by 4%, and negative stage knowledge negatively by 2%. Positive knowledge of negative stages might affect the achievement level positively by 1%, and zero score negatively by 73%. Thus, this variable could affect the achievement level positively by a maximum of 21% and negatively by a maximum of 79%.

Given-asked, free body diagram and formula variables are, for declarative knowledge, independent KLV variables where procedures and rules are determined. The operation variable “Independent KLV”, on the other hand, is the last variable where procedural knowledge is transformed into declarative knowledge using the procedures determined by the three previous variables. Calculations for this variable are given in the fifth column of Table 1. For these variables, positive stage knowledge is thought to affect achievement level positively  by  19%,  unrelated stage knowledge negatively by 14%, and negative stage knowledge negatively by 14%. Positive knowledge of negative stages might affect the achievement level positively by 5%, and zero score negatively by 46%. This variable could thus affect achievement level positively by a maximum of 24% and negatively by a maximum of 76%.

In this research, procedural variables (PVs) were determined by MT2, MT3, and MT4 measurement tools; these calculations were given in the second column of Table1. According to the data in the table, declarative knowledge of prospective teachers about magnetism is affected positively by 34% by the formula knowledge variable (MT2), by 73% by the basic mathematical knowledge variable (MT3), and by 37% by the scientific knowledge variable (MT4). Among these results, the formula knowledge level (PV, 0,34) and the formula knowledge level (KLV, APS= 0,20) is the nearest value for achievement level (ASS=30). The achievement level is most affected by these two variables.

Semiotic findings and interpretations

In the solutions of magnetism problems, maximization of students’ functional behaviors, quality of production (knowledge level and achievement level), and efficiency can be assured by increasing the positive knowledge level in dependent variables. Assuring control in problem solving is also related to evaluation mechanisms. Therefore, independent variables (KLV and PV) are defined as evaluation and control mechanisms. In this research, based on the acquired findings, in order for prospective science teachers to assure maximization of the dependent variable (ASS) in problem solving related to magnetism, correlations of knowledge level in the control mechanism and in the evaluation mechanism will be interpreted. In this research, the fact that the knowledge level of given-asked (KLV) variables, which is the first evaluation mechanism of the prospective science teachers’ problem solving of magnetism topics, is 0.02 (2%), showing that division of the question into its subunits is not done in such a way as to assure optimal benefit. This knowledge level shows that the prospective teachers have completely suppressed option generation by an inert decision. In problem solving of different epistemological levels such as magnetism, an inert decision in given-asked (KLV) variables ceases the partition of declarative knowledge into its subunits. As the knowledge level of this variable is the first obstacle to the solution of the code by establishing semantic coordination among subunits, it shows that synapse 1 is not stimulated. Therefore, the data areis transferred into primary evaluation in the scientific knowledge (PV) knot without partition of subunits and with 0.37 (37%) positive knowledge level. It can be accepted that, in this knot, prospective teachers are self-organized in problem solving and keep this utility function impulsively maximum and stimulate synapse 2. Stimulation of synapse 2, at 0.34 (34%), stimulates the formula knowledge (PV) knot. In this evaluation knot, knowledge formulas related to the data are determined with 34% accuracy. At this 34% knowledge level, in order to reach a solution through formula options in a self-organized way, either the formula knowledge (KLV) control knot is stimulated by stimulating synapse 7 in order to reach the correct formulas (options), or the basic mathematic knot is stimulated by stimulating synapse 3 in order to reach the result by reducing more than one option. As basic mathematic knot synapse 6 is stimulated, therefore, the FBD (KLV) knot is stimulated through it as well, and stimulation of this knot in turn stimulates synapse 8, which controls the reduced options. If, in formula knowledge (PV), knot formulas are determined by maximizing a certain utility function by a risky decision, these formulas stimulate synapse 7, and therefore, the formula knowledge (KLV) knot as well. In this knot, when synapse 10 is stimulated by reducing formula options by 20% through correct control operations, the operation (KLV) knot is stimulated, and synapse 12 is also stimulated in order to reach the result using control mechanisms in this knot. In the present case, in the operation knot, using data (synapse 9) and formulas (synapse 10 and 11), operation options are reduced in accuracy by 19% (operation variable APS), and entropy reduction of control mechanisms must be used. Due to the reduction in the operation knot, synapse 12 is stimulated, and therefore, the result (ASS) knot is stimulated as well. In this control knot, the result is determined by 12% reduction of accuracy. Given these findings, this result might have been reached by stimulating synapse 3. In the present case, in formula knowledge (PV),the knot utility function is maximized by a precautious decision; and therefore, more than one formula is determined and synapse 3 is stimulated in order to determine the formula that will reach the result; and next, therefore, the basic mathematic knot is stimulated. In this knot, a 73% precautious decision option generation is partially suppressed and the evaluation is done; therefore, synapse6 is stimulated. Stimulation of this synapse might then cause stimulation of the FBD (KLV) knot, in which case, using 16% figure drawing procedures and an inert decision, suitable formula options are determined, synapse8 is stimulated, and the result is reached. However, because FBD knowledge level is lower than formula knowledge (KLV) level here, contrary to the high level of knowledge of basic mathematics, the possibility of these final ways of stimulation being used is quite low. These ways are shown in Figure 4. Figure 4 will be called Pictorial Diagram 4.

 

Semiotic discussion and suggestions

In order for a learning system to be successful, option generation, evaluation, variation preservation, and selective omission should be well balanced. The low achievement level of prospective teachers, who use an adaptive learning system, shows that there is not a correct or suitable balance between variation preservation and selective omission. Based on the data acquired, for prospective teachers to be successful in understanding magnetism topics, usage of evaluation and control mechanisms in teaching should be improved. Using the knowledge-based semiotic method developed in this paper could make a significant contribution to facilitating evaluation and control mechanisms of prospective teachers, because this method both models how to separate knowledge into its subunits and models how to understand the code by constructing semantic co-ordination among these subunits. Facilitating working mechanisms using semiotic modeling can increase the achievement of prospective teachers. Therefore, these teachers’ controlled learning or understanding can be assured. If students can adapt to academic objectives and if temporal data is reconstructed in the light of prior knowledge and plans, it is shown in the literature that semiotic models can affect the achievement and creativity of students (Tochon, 1998). Moreover, it is shown that adaptive subject materials also improve the learning achievement of students or the effects of learning (Tseng et al., 2008).

For the improvement of declarative knowledge, it is significantly advantageous to start developing evaluation and control mechanisms of procedural knowledge in order to improve evaluation and control mechanisms, certainly in cases similar to that of this study. After facilitation of procedural knowledge mechanisms, declarative knowledge should first allow balanced decisions using evaluation mechanisms of problem solving and then should balance variation preservation and selective omission in control mechanisms.

The authors have not declared any conflict of interests.