ABSTRACT
This paper presents a procedure in format of a flowchart for prover sizing based on API-MPMS Standard which can be considered as a pattern for prover sizing in field prover design and fabrication. The method was analyzed and verified for the prover of the biggest crude oil fiscal metering system in Iran, that is, bidirectional field prover of Genaveh 10 Million BBL Crude Oil Storage Tanks Fiscal Metering System Project which was designed and fabricated by Asia Instruments Co. LTD. Since this prover was designed to calibrate both heavy and light crude oil fiscal metering systems, each comprised five Ultrasonic Liquid Flow Meters of Faure Herman Co., API MPMS standard requirements for ultrasonic liquid meters were also considered in prover sizing presented method. Results indicate how commercially optimum prover dimensions can be obtained based upon project specifications and other equipment of fiscal metering system and prover.
Key words: Prover sizing, ultrasonic flow meter, detector switch.
The basic principle on which the pipe prover operates is shown in Figure 1. A sphere or piston known as a displacer is installed inside a specific length of pipe and elbows. When the prover is connected in series with a flow meter, the displacer moves through the pipe and forms a sliding seal against the inner wall of the pipe so that it always travels at the same speed as the liquid flowing through the pipe. In some field provers, the displacer is a piston with elastomer or plastic seals; however, in most field provers, the displacer is an elastomer sphere. To provide good sealing, the pipe bore must be smooth with inner coating; at two or more points in Figure 1, there are devices known as detector switches fixed to the pipe wall. These detectors emit an electric signal when the displacer reaches them. The signal from the first detector switch is used to start the electronic counter which accumulates pulses from the meter. When the displacer reaches the second detector, its signal stops the proving counter. The number of pulses shown on the proving counter is the total pulses generated by the meter while the displacer was travelling between the two detectors. Conventional pipe provers (both bidirectional and unidirectional) are those that have a volume between detectors that permits a minimum accumulation of 10,000 direct (unaltered) pulses from the meter. Thus a unidirectional prover typically accumulates a minimum of 10,000 pulses per proving run, and a bidirectional prover typically accumulates a minimum of 20,000 pulses per proving run (including forward and reverse runs). Direct (unaltered) pulses include those that are the output of high frequency pulse generators, considered to be a “part of” the meter. It should also be noted that there are occasions when 10,000 pulses cannot be accumulated during proving passes. This may occur because of a change or a constraint in operating conditions. Agreement between parties to use less than 10,000 pulses per proving pass is required in these instances (API, 2003).

Small volume provers have a volume between detectors that does not permit a minimum accumulation of 10,000 direct (unaltered) pulses from the meter. Small volume provers require meter pulse-interpolation techniques to increase the resolution (API, 2008) This high resolution pulse determination permits the volume between detector switches to be substantially less in a small volume prover than would be permitted in a field prover. Additional information on small volume provers is contained in (API, 1998).
The turbulent flow field in a pipe is complex and contains numerous turbulent eddies and non-axial velocity components. Turbine meters and other mechanical flow measurement devices integrate this field through mechanical convergence and are not particularly influenced by minor changes in flow stability. Fluid acceleration into the rotor combined with rotor mass produces mechanical integration of the flow field. Ultrasonic Flow Meters (UFMs) take snapshots of the fluid velocity along one or more sample paths. Each ultrasonic path is a line of sampling that produces time differentials and subsequent velocities as snap shots equal in number to the sample frequency for the sample period. Variations in velocity along each path are random as the turbulent eddies and variations in local flow that produce them are entirely random. Each sample will then vary from the mean velocity for a given sample period and the family of samples will be evenly distributed about the mean. UFMs “see” not only the global axial velocity, but also all of the flow components, including the turbulent eddies resulting from fluid drag and mixing in the pipe. Verifying the performance of a UFM is not unlike verifying mechanical systems. However, because UFMs employ sampling methodology, they produce a greater degree of data scatter due to their ability to measure minute variations in velocity. UFMs may produce wider repeatability ranges for existing provers designed in accordance with industry standards than are typical for a mechanical device. Failure to be mindful of the evenly distributed nature of the data points about the mean meter factor will lead to errors in evaluation. A range exceeding 0.05% in 5 runs does not mean that a UFM is defective, or that its meter factor cannot be established with the required uncertainty.
UFM performance verification can be ascertained by conventional means and to a level consistent with (API, 1995). (Table A.1 of API (2005) and Table B.1 of API, 1995. The most conservative approach to accomplishing this level of repeatability relies on determining an acceptable prover volume. For instance, turbine meters can usually be successfully proven in 5 consecutive runs to within 0.05% span of repeatability, which demonstrates ± 0.027% or better meter factor uncertainty at a 95% confidence level. Table A.1 of API (2005) provides the guidance for obtaining these results. Any of the number of runs chosen from that tabulated data will produce results that verify meter performance to ±0.027 % uncertainty. There is no difference, in this regard, in a repeatability range of 0.05% in 5 runs vs. a range of 0.12% in 10 runs; they are the same. The operator is advised to select the appropriate number of runs, and span of repeatability, suitable for the prover volume available. Alternatively, the operator may simply increase the number of proof runs incrementally until the repeatability range falls within the limits of Table A.1 of API (2005). Larger numbers of runs may be necessary if small volume provers are employed. Small volume provers that create flow disturbances can create non-repeatable proving results. Care shall be exercised when selecting and using small volume provers API (2005).

Proving accuracy can be affected by the delayed manufactured flow pulses from a UFM. These delayed manufactured flow pulses can lead to a bias error in the calculated meter factor depending upon the magnitude of the flow rate change that occurs during the proving run and the duration of the prove run. This potential problem is explained in detail in Annex C of API (2005). Master meter proving of an ultrasonic meter as per (API, 2011) may be applied, provided the additional uncertainty typically associated with master meter proving is acceptable to the parties involved. Some UFMs may produce a non-uniform pulse output, which can exhibit a wide span of repeatability when proved. See Annex B of API (2005) for detailed explanation. It should be noted that proving run repeatability might not fall within the typical 5 run, 0.05 % span of repeatability. However, proving runs shall repeat within the guidelines of API, 1995.
Zeroing an UFM (or as so called in gas applications "zero calibration") is a procedure that involves checking the output while the meter is blocked-in. Under these conditions, and if the output of the meter does not indicate zero flow, then the manufacturer’s re-zeroing procedure shall be followed. Whenever the meter is re-zeroed, it shall be reproved. Normally, a UFM does not require manual zeroing. However changes or replacement of acoustic transducers, electronics or acoustic transducer cables shall require that the meter zero be checked and if necessary re-zeroing procedures shall be followed. In any case, changes or replacement of acoustic transducers, electronics or acoustic transducer cables shall require the UFM to be reproved. The distance between the acoustic transducers are known (path length) and therefore by knowing how long the signal takes to cross that distance, a velocity of sound measurement can be made. The approximate velocity of sound range for Crude Oil as a case in point is 4,400 ft/s through 5,000 ft/s; by knowing the velocity of sound and comparing to what is determined by the meter, the velocity of sound on each path should be similar indicating a consistent product stream. Paths showing a change in velocity of sound may indicate a change of product in the stream. A velocity of sound variation from top to bottom of the meter could indicate a density gradient (API, 2005).
Bidirectional provers can use either a sphere or a piston as a displacer. Spheres are more commonly used because they will go around bends, and the prover can be built in the form of a compact loop. A four-way valve is normally used to reverse the flow through the prover. The sphere will start to travel on its return pass when the four- way valve begins to reverse the flow, but it will not reach its full speed until the movement of the four-way valve is complete. Displacer detectors are never quite symmetrical in their operation, and consequently the effective calibrated volume when the displacer travels between detector 1 and detector 2 will not be quite the same as when the displacer travels between detector 2 and detector 1. That is why bidirectional provers use four detector switched, two for forward runs and two for reverse ones. The calibrated volume of the prover is the sum of both directions and is termed the round trip volume, and the prover counter totals the pulses collected in both directions. The detectors fitted to a pipe prover are highly sensitive devices. The most common type of pipe-prover detector switch uses a ball-end steel plunger, which projects through the wall of the pipe a short distance. When the sphere makes contact, it forces the plunger to actuate the switch.
Although for sphere displacers maximum speed, most operators and designers agree that 10 fps and 5 fps are typical design specifications for unidirectional and bidirectional provers respectively, higher velocities may be possible if the design incorporates a means of limiting mechanical and hydraulic shock as the displacer completes its pass. On the other hand, displacer should move at a uniform velocity between detectors. At low velocities when the lubricating ability is poor, the sealing friction is high, and/or the prover Surface is rough, and the displacer may chatter. Typical minimum sphere displacer velocities for lubricating fluids are 0.5 ft/s – 1.0 ft/s (API, 2003). So, care should be exercised to reach minimum speed of 1 fps in order to prevent from any leakage through ball.
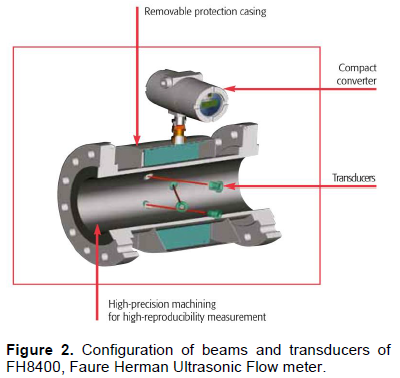
Bidirectional field prover of Genaveh 10 Million BBL Crude Oil Storage Tanks Project which was fabricated to work in conjunction with the hugest Oil metering system in Iran is considered as case study of this project while corresponding metering systems comprises ten Faure Herman flow meters (five for light and five for heavy crude oil metering). Using the most innovative ultrasonic technology, the FH8400 Product (IDEX Liquid Controls Group, 2016a), manufactured by the French manufacturer, Faure Herman, successfully covers a wide range of applications and flow conditions including laminar, turbulent, asymmetric flow velocity profiles and swirls. The FH8400 ultrasonic flow meters "Transit Time Difference Method" are designed for process applications of all liquids, crude or refined hydrocarbons, whose viscosity is lower than 180 c.St., including LPG. Considered meter in this study has 3 beams, 6 ultrasonic transducers interchangeable under service conditions as illustrated in Figure 2, ±0.15% accuracy, ±0.027% uncertainty, anti-swirl effect and Flow profile compensated (Multi product). For a given size, the recommended K-factor has been adjusted to provide the best measurement precision. The factory-set K-factors are depending on size of meter as per Chapter 1 of (IDEX Liquid Controls Group, 2016b) Utilized meter is 12” in size and its flow range is 240 to 2,400 m3/h (turn-down ratio of 1:10) and K-factor of 4000 pulses/m3 approved by NMI and is compliant with OIML R117-1 (edition 2007) specifications.
Thanks to high-speed electric motor actuators, a Four-way valve of American manufacturer, Cameron, is used in this case study. Pre-run length of a field prover significantly depends on traveling time of four-way valve; the more quick-opening four-way valve, the less pre-run and hence lower field provers volume. Typical self-locking electric motor-operated valve speeds are limited; therefore, by reducing the number of turns required with the speed increasing gearbox (SIGB), actuation time can be significantly reduced (Figure 3). Figure 4 indicates a four-way valve during traveling while slips are rotating, and so flow direction is being reversed.
While the valve is seated, the flow streams are completely separated and sphere can reach to its maximum velocity, whereas rotation of slips leads to reduction in sphere velocity and stop.
As the valve is unseated, the plug is raised and both slips are retracted, causing the plug and slips to begin to turn. Then the slips and resilient seals are fully retracted away from the body. In this study, required time to reverse the flow in bidirectional prover through motorized Cameron four-way valve is 15 s. As dominant item of a prover is its four-way valve, it is highly recommended to be zero leakage in order to prevent from additional uncertainty during proving and to be designed as per ASME B16.34 and API6D Standards.
Detector switches are one of the imperative items in determination of prover Calibrated volume; it can be inferred that more repeatable results can be gained via more accurate detector switches, and consequently less base volume can be considered for a prover during sizing; this principle is illustrated in calculations of this paper. Four Detector Switches of FMC Co, model B5-A are considered for field prover of Genaveh 10 Million BBL Crude Oil Storage Tanks fiscal metering Project, two switches for forward runs and two for reverse ones. These detector switches have the repeatability of 0.0127 mm, actuation set point of 6.0000 mm, plunger diameter of 17.0000 mm (Figure 5), and resulted maximum and minimum detector actuation depth of 6.0127 mm and 5.8973 mm respectively.
METHODOLOGY OF PROVER SIZING
In present work, a combination of basic information in API, 2003 and API, 2005 is prepared as a procedure in order to find the optimum dimensions of a prover to be matched with a fiscal oil metering system comprising 10 meter runs each incorporating a UFM passing requirements of API-MPMS standard. After having all required data of UFM, four-way valve and detector switches, in step 2 of the presented flowchart of Figure 7, as can be seen, minimum and maximum capacity for which the prover is being designed (Qmin & Qmax) shall be also given as input data to flowchart; these quantities whether can be considered as minimum and maximum capacities of metering system divided to each meter run or measuring range of UFM; still, certainly flow meter measuring range has a wider span in comparison with metering system capacity, leading to larger prover size. In this case study, metering system design capacity is considered for minimum and maximum flow rates for prover design which were 480.0 m3/h. and 2,270.0 m3/h for each meter run. Then, as first guess for prover diameter, a relation in Equation 1 is offered which leads to minimum guessed diameter possible for prover considering maximum displacer velocity (Vd,max) as per step 2 of Figure 7; afterwards, as prover has to be fabricated via nominal pipe sizes available in market, the next standard size of pipe as per API-5L and client's piping specifications can be considered as Dp (step 4). Since so far the minimum diameter possible for prover is selected, one should check for the maximum and minimum velocity criteria not exceeding the standard limitations as per step 6 of procedure. So, the first diameter that passes velocity criteria will be the minimum candidate diameter for pipe of prover; should a diameter be rejected in step 6, next higher pipe size (according to API 5L) shall be considered; this process will continue till appropriate and optimum pipe size be selected.

After finding the proper diameter, minimum length between detector switches shall be found bearing in mind that there are three limitations for this length. First is supporting number of maximum pulses for which prover is being designed. As field provers are designed to carry out 10,000 pulses between detectors, considering 5% safety factor for this length, it can be presented as per Equation 3 (step 7 of Figure 7).
Next criterion for Calibrated volume of prover length is satisfaction of repeatability and accuracy of detector switches. For this purpose, displacer position repeatability (∆Xm) which is a function of range of detector (plunger) actuation repeatability (I1–I2) shall be calculated as per Equation 4 (step 8 of Figure 7), minimum length corresponding to this length and number of detectors can be determined according to Equation 5 in which NDet shall be considered 2 and 4 for unidirectional and bidirectional provers respectively.
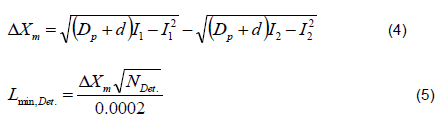
The third limitation for length between detector switches is passing criterion mentioned in API, 2005. As detailed discussed in introduction, based on field data, UFMs may require a larger prover volume to achieve the same level of meter factor uncertainty; the reason why this fact happens is that in contrast with inherent pulse producing behavior of turbine or PD meters, ultrasonic meters produce artificial signals which may be non-uniform. In fact, in a UFM, pulse generation is done by means of a digital-to-frequency converter. Since the frequency is generated as the result of a measurement, it always lags the flow by the update period. As can be seen in Figure 7, small sized provers connot be utilized for calibration of ultrasonic meters as UFMs may produce non-stable output frequency which cannot be interpolated like the pulses produced by turbine and PD meters. In Figure 6, pulse pattern of both ultrasonic and turbine meters are illustrated each for three experiments revealing that during pulse interpolation repeatability is 0.011 and 0.23% for turbine and ultrasonic meters respectively. Despite outrageously non-repeatable for ultrasonic meters because of non-uniform pulse generation pattern, pulse interpolation leads to acceptable repeatability for calibration of a turbine meter.

Given the larger prover volume that may be needed to verify a UFM to ± 0.027 % uncertainty, it follows that more than 5 proving runs may be required to verify the meter’s performance. Experience with UFM’s of several manufacturers using ball provers shows that the required meter factor accuracy is typically achieved with fewer than 10 to 12 runs, or with a prover volume larger than current industry standards for other types of meters such as turbines. For applications where the use of a large prover is not viable, master meter proving of an ultrasonic meter according to API (2011) may be applied. So, in this design, 10 runs of proving were considered in order to meet requirement of ± 0.027 % uncertainty as per (API, 2003). Steps 10 and 11 of Figure 7 indicate the method to pass uncertainty restrictions.
After all these calculations, one can easily determine the length of straight pipe and number of elbows and flanges required for a prover.
RESULTS OF PROVER SIZING FOR CASE STUDY
After programming and application of methodology previously presented to design prover for Fiscal metering system of Genaveh which totally comprised ten UFMs, prover sizing was done in detailed design stage at Asia Instruments Co LTD and results were given as per below table, and based on them fabrication of prover was done.
Table 1 presents the raw results of optimum prover which was designed and constructed in Asia Instruments Co Workshop indicating that determining factor in base volume of prover is API-MPMS 5.8 criterion; in fact, the answer to Equation 7 would be LMPMS 5.8. As can be seen in Table 1, optimum prover base volume diameter has been emerged to be 30” in diameter; even though couple of higher sized may still pass the criteria of displacer velocity (step 6 of Figure 7), the minimum possible diameter can be the best commercially optimized diameter for prover. In order to validate that Table 1 results are the optimum sizing results, next pipe size available in market, that is, 36” is considered as prover designed base volume diameter, and procurement of main items of 30” and 36” provers are compared commercially. This comparison is claimed to be used for validation of methodology offered in Figure 7 since this flowchart finds least allowable diameter for base volume of prover based on displacer velocity criteria (step 4 to 6 of Figure 7). So, suppose that the prover base volume is 36” in diameter; in this case, at first glance, if one calculates only the pipe consumed for the base volume and pre-run sections from Tables 2 and 3, it can be found that net mentioned material with 36” pipe will be more economical than that of 30” since length of pipe would reduce significantly for larger size; however, the reason why the smallest pipe size for prover is selected in procedure is that the main components of a prover such as flanges, elbows, reducers, displacer, launchers and quick opening closures (illustrated in Figure 8) are normally more expensive than pipe; so, their price will increase dramatically with size.
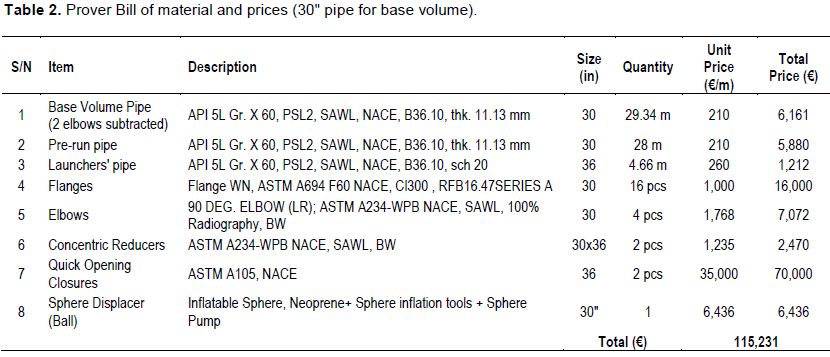

It could be inferred that a cost analysis is required in order to compare 30” and 36” provers; therefore, in Tables 2 and 3 detailed cost analysis for all main items of these two sizes are given.
Although neglecting increment in price of welding consumable materials, welding labor costs, stud bolts and nuts, gaskets, foundation and gratings, overhead cranes, etc. with size of base volume pipe, as can be seen in Tables 2 and 3, price of a prover with 36” pipe for the same base volume and operating conditions is 18% higher than that of 30”. Figure 9 shows manufactured prover with 30” base volume pipe diameter which is the optimum diameter from project commercial point of view. It worth to mention that minimum possible diameter for prover is not only the optimum case in cost analysis point of view, but also experience revealed that the less diameter the ball has, the more smooth it turns around the bends with minimized leakage.
Optimum diameter and length of pipe provers are two dominant items which should be determined during prover sizing in order to both optimize the material used for prover and have reliable calibration results after each proving in future. In this study, a procedure is proposed to calculate the optimized prover sizes based upon specifications of project. As can be seen in results, pipe is determined to be 30” in diameter after some iterations according to the loop illustrated in Figure 7. Also, it can be inferred from Table 1 that the determining factor in prover base volume is uncertainty criterion for a UFM; also, the required base volume for satisfaction of detector switches uncertainty was only 4% of the required volume for UFM uncertainty. It can be inferred from this paper that drawback for liquid UFMs is large prover sizes in comparison with turbine and PD meters since pulse instability and uncertainty requirements of UFM caused the large base volume during design.
Finally, it is validated that the minimum possible diameter passing requirements of displacer maximum and minimum speed according to standard is the most economical diameter which can be selected for base volume and pre-run sections of prover and can be calculated based on proposed approach.
The authors have not declared any conflict of interests.
REFERENCES
|
API (1995). Proving Systems, Operation of Proving Systems, First Edition, API, Manual of Petroleum Measurement Standards. 4(8).
|
|
|
|
API (1998). Proving Systems, Small Volume Provers, First Edition, API, Manual of Petroleum Measurement Standards (MPMS). 4(3).
|
|
|
|
|
API (2000). Specification for line pipe, API specification 5L, Forty-Second Edition.
|
|
|
|
|
API (2003). Proving Systems, Displacement Provers, Third Edition, API, Manual of Petroleum Measurement Standards (MPMS). 4(2).
|
|
|
|
|
API (2005). Metering, Measurement of Liquid Hydrocarbons by Ultrasonic Flow Meters Using Transit Time Technology, First Edition, API, Manual of Petroleum Measurement standards. 5(8).
|
|
|
|
|
API (2008). Proving Systems, Pulse Interpolation, Second Edition, API, Manual of Petroleum Measurement Standards (MPMS). 4(6).
|
|
|
|
|
API (2011). Proving Systems, Master Meter Provers, Third Edition, API, Manual of Petroleum Measurement Standards. 4(5).
|
|
|
|
|
FMC Technologies (2002). Bulletin SSPP006, Sphere/ Pig Detectors, FMC Technologies.
|
|
|
|
|
IDEX Liquid Controls Group (2016a). Catalogue of Ultrasonic Custody Transfer Flow Meter for Light & Medium Viscosity Products, FH8400, Faure Herman Co., IDEX Liquid Controls Group.
|
|
|
|
|
IDEX Liquid Controls Group (2016b). User's manual of The Ultrasonic Custody Transfer Flow Meter for Light & Medium Viscosity Products, FH8400, Faure Herman, IDEX Liquid Controls Group.
|
|
|
|
|
Syrnyk P, Seiler D (2007). Use liquid ultrasonic meters for custody transfer division. Hydrocarbon Processing, 91-96.
|
|