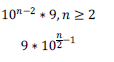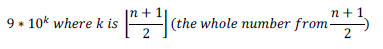Patterns and generalization are one of the most fundamental aspects of mathematics, which makes recent decades, mathematical tasks which include patterns, whether they are numerical or graphical, are mostly used, for example researching generalization. The aim of this paper is to investigate how a special kind of task concerning well-known palindromes can diversify the process of generalization in three different age groups of students. More precisely, the paper includes the analysis of solutions of one task concerning counting of numbers of palindromes by middle school, high school and university students with the special attention for finding similarities and differences among advance of process of generalization and using methods of solving in researched groups. The researched groups chosen randomly from two distant part of Poland, were consisted of 44 middle school students, 102 high school students and 51 university students (including 42 pre-service teachers). All students solved the same task in limited time without any assistance of teachers. The research was carried out between 2013 and 2015.
Learning mathematics in the whole world is liable to constant reforms. Following the Program for International Student Assessment (PISA) and experts who analyzed the obtained results, one has to accept the need for a change in the students’ attitude towards learning mathematics and developing a habit of observation, conducting experiments, establishing findings without assistance, and gaining information.
According to (Krygowska, 1981), we can identify at least several mathematical activities: perception and use of analogy, deduction, the reduction of problems, the assimilation and transformation of data, schematization,
discovering regularities, and generalization.
Generalization can be recognized as a characteristic of mathematical thinking. This process is useful to extend notions (the class of notions), that is by defining a more generalized notion, which one can obtain by indicating a “super notion”, weakening the defining conditions, generalizing the relation connected with the notion, using the mathematical induction principle, or unifying particular cases (Tocki, 2006).
Tocki (2006) further writes that the process of generalization can be considered in two aspects. On the one hand, it is to find a common (constant) property of objects or relations; and on the other hand, to specify a particular property in the examined object and to create a class of all objects which have this property. Generalizations on theorems by weakening the assumptions, strengthening the thesis, introducing parameters, or unifying or changing the proof, can be performed (Tocki, 2006).
The need for teaching such an activity was raised in (Krygowska, 1977). Undoubtedly, the crucial basis in the process of generalization which is the proper choice of tasks, consists of not just choosing stereotypical ones for which the student already knows the algorithm of solving it but ones for which the student is forced to find their own way of solving the task by using acquired knowledge.
Transitioning from stereotypical tasks to open problems was attempted in (Wittmann, 1972), (see also (Krygowska, 1977)). Wittmann’s research is concerned with students’ observations when solving open problems in which they can be assisted by their teacher. By performing an analysis of the students’ work, he concluded that this way of thinking as well as the students’ imagination is lifted up to a “higher level of energy“(Krygowska, 1977).
The consequence of such a procedure was the possibility of “extending” the problem posted in the task. One of the forms of extending the problem, as Krygowska writes, is the specification or the generalization of previously learnt theorems. Specification, as defined by Krygowska, is formulating particular cases of a given theorem, and generalization is formulating a theorem for which the special case is a given theorem. If we do not know whether the theorem is true or false, specification can help us decide on the question.
One of multiple task type is a task which includes patterns as the main objects described in the text of the task. Relating patterns in geometry, algebra, and measurements undoubtedly help students in understanding many of the connections among different mathematical topics.
As emphasized in Hale (1981) and Hargreaves et al. (1998), recognizing, describing, or extending patterns has considerable value in the introduction to formal algebra. This statement is based on many investigations. For example, Schoenfeld and Arcavi, (1988) indicate that “by asking students to observe and summarize them [patterns] verbally and we may help make the transition from arithmetic to algebra”. Furthermore, Tanisli and Ozdas, (2009) emphasize that pattern activities are important parts in the introduction of algebra, especially for young people.
Guerrero and Rivera, (2002) states that pattern are a kind of rule among the elements of a series of mathematical objects which are constructed. Moreover, according to Burns (2000), a pattern is the key concept for understanding and observing mathematical relationships (Tanisli and Ozdas, 2009). Other examples can be found in Tanisli and Ozdas, (2009).
Working with patterns in geometry usually leads to the generalization of a sequence of numbers. It is significantly easier for the students when the patterns (or some of its initial steps) are included in the text of the task.
As was shown in (Jureczko, 2104), high school students can also generalize patterns (which led to some sequences of numbers), which are partially described verbally in the task, with some initial steps given as auxiliary sketches. The task, which in that research concerned the so-called steric numbers, was very important. In order to solve it, the students were required to provide a general rule dependent on two variables. Although the task was solvable for high school students, younger students might have found it to be too difficult.
In Jureczko, 2016), the author investigated a group of more than 100 people divided into three groups: middle school students, high school students, and university students. But this research differed from Jureczko, 2014a), because the students were given a task concerning operations with cubes without any auxiliary sketches of the situation described verbally in the tasks.
Despite this, a number of students made such sketches of the cube in their solutions, which undoubtedly helped them solve (though partially) the task. What is worth noticing is that, although all of the researched students had sufficient mathematical knowledge for solving the task. The number of proper and full solutions was small and increased proportionally to the age of the researched groups (that is the smallest amount of proper solutions (or even some parts of the task) was among middle school students; while almost all university students provided full solutions for the task, even though not all of them gave a comprehensive explanation of how they reached the solution).
According to Hargreaves et al. (1998), some of the research regarding children working with patterns (students aged 11 to 15) shows that it is more difficult for them to explain patterns than to continue them and a significant number of pupils performed the generalization of the pattern by using only partial information from the previous steps (This also occurred in the research analyzed in (Jureczko, 2016).
The process of generalization of patterns may be useful in other more advanced aspects of mathematics. As shown in Jureczko, 2014) and Jureczko, 2015), generalization in the presence of IT aspects, such as graphic display calculators or equivalently mathematical computer software, can be used as an alternative and, most likely, more intuitive introduction to calculus (It is worth emphasizing that the topics concerning calculus belong to “higher planes of abstraction” which are not achieved by all young people in high school).
Obviously, the mathematical and analytical explanations of such objects as the limits of functions (especially when simple algebraic calculations lead to symbolic representations) or its derivatives can undoubtedly help students in understanding the sense of the mathematical operations they have to do when solving a particular problem using calculus.
Another way of working with numbers, which is called pattern generalization, was investigated in (Bojarska-Sokołowska, 2014), where the author described the analysis of research regarding children aged 8-9. The task concerned platonic solids, for which the students were asked to calculate the edges, vertices, and faces, as well as deduce the relation among these numbers. It was most likely the first time the children had contact with variables, but the best results were obtained by using concrete numbers for each of the mathematical objects.
Another direction of research in the topic of pattern generalization is studies regarding pre-service and in-service teachers. For example, Zazkis and Liljedah, (2002) presented research regarding pre-service elementary school teachers, whose task was to continue a pattern of numbers arranged in a kind of matrix. The participants were also asked to provide the rule for generalizing the numbers occurring in the pattern (that is they had to predict the appearance of a particular number in the matrix). As shown, the continuation of the pattern turned out to be easier than performing the generalization.
Furthermore, the participants lacked synchronization between the demonstration of algebraic thinking and the ability to use algebraic notation. There was a gap between the ability to express generality verbally and the ability to employ algebraic notation. This research showed that the gap does not disappear, although in Jureczko, 2016), the problem did not occur among university students who were studying mathematical sciences. Other examples of research regarding teachers’ attendance can be found for example in the study of Chua and Hoyles, (2009) and Rivera and Becker (2007).
Many authors (i. e. Hargreaves et al., (1998) carried out research using tasks which led to the generalization of a sequence of numbers and usually provide consecutive numbers in the given sequences (which Rivera defines
as near generalization, as opposed to the general pattern, which Rivera calls for generalization).
The author of this paper does not know of any researchers who would touch the problem of other number patterns. This led the author to decide to investigate how students work with other number patterns, for example palindromes consisting of numbers of a different length. The author in this paper posed the following research questions:
(1) What kinds of methods were used in order to obtain generalization?
(2) How does the process of generalization look like depending on the age of participants?
(3) What kind of common characterizations occur in each age group? What kinds of characteristics differ in these groups?
(4) Are the tasks concerning generalization interesting for the students?
Data collection and analysis
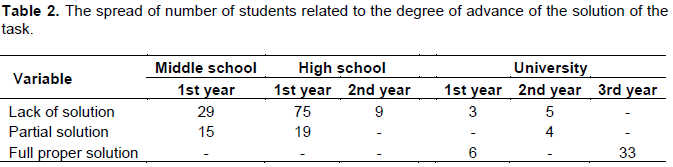
The goal of the research was to investigate how students of three different age-groups (middle school, high school and university) interpreted and solved the following task (Table 1).
197 participants took part in the research, divided into three age groups: 44 middle school students, 102 high school students, and 51 university students studying mathematical sciences (including 42 pre-service mathematics teachers). Students came from two distant parts of Poland (East-North and middle) between years 2013 and 2015.
All of the students were given the same 45-minute limit to solve the task during the lesson or lecture. The students were not assisted by any coordinating teacher. The coordinating teachers were not allowed to provide any hints or disturb the students when solving the task. The research was carried out on several groups.
Table 1 presents division of participants divided by age group: middle school, 13-15 years old; high school, 16 to 19 years old; university, 20 to 22 years old (2nd and 3rd year) and the degree to which the task was solved (lack of solution, partial solution, full proper solution) (Tab 2).
As presented in Table 2, the students were divided into three age groups. Hence the analysis also being divided into these three groups.
Students of middle school (year 13 to 15)
Students from this group mainly base their solution on writing down all possible palindromes, which is why almost of them gave the proper number of palindromes composed of one and two digits. It is worth noticing that although they had taken into account the palindrome “0”, they erased the palindrome “00” without providing any explanation.
This method proved not to be efficient in further cases, which is why the answers for further questions were provided only by nine of the fifteen students who touched upon the problem. The students, encouraged by the lack of difficulty in the previous cases, attempted to write down the palindromes composed of three digits but mainly in the form of perhaps “111”, ”222”, etc. in which all digits are the same. It was probably due to the influence of the previous steps.
Two of the students, making use of this observation, answered that there are only nine three-digit palindromes. One of the students continued this process, giving the same answer for four- and six-digit palindromes. However these students did not generalize this matter for n-digit palindromes, answering that there was an infinite number of such palindromes.
Five other students tried to write down the other three- and four-digit palindromes, and two of them answered that there are 100 three-digit palindromes, but for longer ones they concluded that there are “infinitely many of them” or “a lot of them”. Two students’ solutions are worth special attention.
Figure 1 presents a part of a student’s work showing their reasoning as regards calculating the number of palindromes of different types. The student, despite proper observation regarding number of one- and two-digit palindromes, as well as proper observation of the structure of further cases of palindromes, did not resolve the number of the longer ones.
In contrast to the previous case, the next participant (Figure 2) provided an algorithm with which one can calculate the number for further cases of palindromes by writing “10 for each number in the front”. This means that the student builds consecutive palindromes by inserting a digit as the front. However, it is worth noting that by writing “10”, the student did not take into consideration palindromes starting with “0”.
In this group, no student provided any generalization of n-digit palindromes, though some of the students were willing to continue working on this task by asking the questions: “How many eight-digit palindromes are there?” “How many 10-digit palindromes are there?”, “Is there a palindrome that consists of 3 digits, for which the sum of digits equals x?” “Are palindromes odd or even?” No student answered the question on the existence of a common divisor for all of the palindromes.
High school students (1st grade)
In this group of students, six only provided the proper number of palindromes for the cases in part a) of the task. There are some differences depending on whether they had taken the existence “0” in a palindrome into account or not. Three of the students provided the number of palindromes, which were unfortunately incorrect (that is, one-digit – 10, two-digit – 100, three-digit – 100, four-digit – 1000).
Four other students used the same method of calculating the number of palindromes as observed among the middle school students by writing down all of the cases, but none of the students concluded any results. In one other student’s work, the student noticed that the number of palindromes from each previous step can be multiplied by 10 in order to obtain the result. This student reached the result by using observation, which is shown in scan (Figure 3).
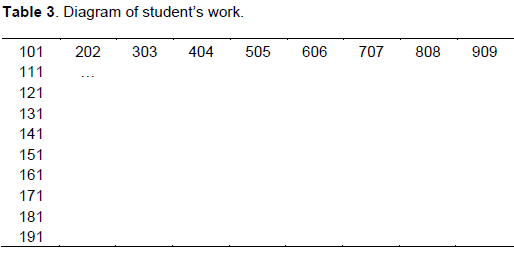
Another type of solution also appeared in the aforementioned student’s work. The student used the matrix in Table 3 when calculating the amount of three- and four-digit palindromes:
Hence they deduced that there are 10x9 = 900 palindromes.
In this group of students, there were two trials of generalization in the forms
but without any explanation or division of n into odd or even, aside the first pattern case resulting from the improper observation that there are 10 one-digit palindromes, 9 – two-digit, 90 – three digit, 10*10*9 four-digit, due to there being 10 times more palindromes in consecutive cases. The student continued her calculations by concluding that there are 10*10*10*10*9=90000 six-digit palindromes.
The second generalizing pattern was not supplemented by any explanation. Similarly to middle school students, no answer was provided concerning the existence of a common divisor. Nonetheless, the following questions
were given in order to continue the task:
(1) “How many four-letter palindromes do you know?”
(2) “Are palindromes irrational?”,
(3) “Is there a number of digits for which the number of palindromes will be infinite?”,
(4) “How many seven-digit palindromes are there?”, “Are there 15-digit palindromes that consist of non-decreasing digits?”
The 2nd grade high school high school did not introduce anything new to the research, which is why this part of the analysis will be omitted.
University (1st year)
Three of the participants used the same method as the middle school and high school students of writing down all of the possibilities of one- and two-digit palindromes, but no generalization occurred.
Three other students described verbally how one can calculate the number of palindromes of particular types, but only two students’ reasoning resulted in the number of palindromes due to pattern generalizing. Unfortunately, both of them are incorrect (Figures 4 and 5).
Unfortunately, the generalizing pattern, although constructed well for n=3 and 6, was incorrect for n= 4. As one can observe in Figure 5, the students (consciously or not) used variations with repetition by taking into account the fact that the digit which cannot be in the first position in the palindrome is “0”.
University students (2nd year - pre-service teachers)
In this group, only one person performed generalization, but the pattern was incorrect, which is why this case was not analyzed here.
University students (3rd year - pre-service teachers)
28 out of 33 students performed the generalization of the problem posted in the task. The solution presented in this group can be divided into three types.
Type 1: Four students used an algorithm similar to a few of the high school students by writing down the possibilities of the arrangements of digits in the palindromes and setting them in a matrix (as was shown in Tab. 3). This way, they calculated the number of palindromes to the ones four-digit. For six-digit palindromes, they changed the algorithm, as they observed that the previous result has to be multiplied by 10. Such reasoning led them to the generalizing pattern in the form of
Type 2: Eight of the students did not provide any explanation for how they reached the generalizing pattern, but they provided a pattern similar to the previous ones or as a hybrid function for n-odd and n-even separately. Some of the students took into account palindromes starting with a “0”, defining the generalizing pattern as a power of 10, depending on n.
Type 3: This group was the most numerous - 16 students. These students used variations with repetition in their reasoning. Four of them, despite proper reasoning, provided incorrect generalizing patterns. Eleven students used the pattern for the variations with repetition in their reasoning, following the process as can be seen in (Figure 6) providing the pattern either for n- odd and n– even separately, or using the notation
It is worth emphasizing the following solution (Pic.7), in which a student partially wrote down the particular cases of palindromes and partially used the rule for the variations with repetition. Three other students formulated a theorem concerning the number of palindromes, in the proof of which they used the mathematical induction principle. The theorem is in the form of:
Theorem: If n is natural and different from 0 and 1, we can calculate the number of n-digit palindromes using the rule , but for n=1 the number of palindromes is equal to the number of all digits.
As was indicated in the Introduction, the goal of the research was to find answer of the following questions:
(1) What kinds of methods were used in order to obtain generalization?
(2) How does the process of generalization look like depending on the age of participants?
(3) What kind of common characterizations occur in each age group? What kinds of characteristics differ in these groups?
(4) Are the tasks concerning generalization interesting for the students?
The process of the generalization of the problem posted in the task is also increasingly proportional to the age of participants. In contrary to the research analyzed by in (Jureczko, 2016), in this task the author provided examples of palindromes in the text of the task, which turned out to be very helpful in the process of formulating the generalization. Generalization on middle school level is limited only to simple observations that palindromes may be constructed by adding the first (and simultaneously last) digit and that there are 10 possibilities.
The students in this group could not provide the general pattern describing the number of palindromes depending on n-length palindromes. Very few students provided the proper number of palindromes of the length of at least 3. However, they usually summarized that there are a lot of, or an infinite number of, palindromes longer than 2.
It is worth noticing that the students, while trying to provide the number of palindromes, wrote down all possible examples, but the method did not prove to be sufficient enough to generalize the problem posted in the task.
This method (consisting of writing down examples of palindromes) was present also among a small group of high school students. While these students did not provide any generalizing patterns, other students provided their attempts of generalization by using alternative methods.
In the researched group of high school students, two other methods occurred: the second one made use of (probably unconsciously) variations with repetition (by observing the general scheme of the palindrome as a system of boxes with digits in each of them), and the third method included entering all possible examples of palindromes (of the length 3) into a matrix, as shown in Figure 7 (the number of palindromes was obtained by multiplying the number of rows by the number of columns in the matrix). The second method especially led to some generalizations (by providing a simplifying pattern).
It is worth emphasizing that although among middle school students, the attempts of generalization were described verbally. Here, in the group of high school students, the first attempts at explaining generalization algebraically were made.
A fully formed process of generalization can be observed among university students (the only participants to reach this conclusion in the research) who used variations with repetition which led them to generalizing patterns (The two other methods mentioned above also occurred, but in the case of very few students).