ABSTRACT
Representation is an important aspect of learners in building a relational understanding of mathematical concepts. But the ability of a mathematical representation of students in building relational understanding is still very limited. The purpose of this research is to description of mathematical representation of students who appear in building relational understanding on concept of area and perimeter of a rectangle. This research is a case study. The research instrument is tests and interviews. The participants in this study were Grade seven students. Two students are selected based on the characterization of the mathematical representations that appear. The study results a visual and symbolic representation used by students in building relational understanding on the concept of area and perimeter of a rectangle. Visual and symbolic representation suggests students to build relational understanding.
Key words: Representation, relational understanding.
National Council of Teachers Mathematics (NCTM, 2000) explains that the learning process of mathematics should emphasize student to enable them to learn with understanding, actively building new knowledge from experience and knowledge. Effective mathematics learning requires students' understanding of what they know and what they need to learn and then provide challenge and support them to learn more. The understanding can be done by reviewing the results of the representation of the students in understanding and solving a mathematical problem. Representation is an important aspect of the learners in developing mathematical understanding. Each student has a different way of building understanding so it allows students to form various types of representations in understanding the concept. In NCTM (2000) there are five standard processes, namely problem solving, reasoning and proof, connection, communication and representation. Representation as one of the standard process, it is because the representation of the mathematical knowledge construction process that is very important to develop and optimize the ability to think. Besides mathematical object more abstract and require representation to understand mathematical ideas.
Representation is the disclosure of mathematical ideas by using various means such as spoken language, written language, symbols, pictures, diagrams, models, charts, or using physical member (Goldin, 2002). NCTM (2000) explains that the use of a mathematical representation forms, such as charts, graphs, tables and symbols as well as transition between the representation of an important capital in expressing mathematical thinking. Use of representation reinforces students' understanding to construct concepts and solve problems in mathematics (Tripathi, 2008; Stylianou, 2010; and BAL, 2014). So in the learning process of mathematical representation is one aspect that must be emphasized. This is due to the ability of a good representation of the students then students can expand its capabilities in solving mathematical problems. Research related to the importance of representation in mathematics, among others, performed by Dündar (2015), BAL (2014), Villegas (2009), these studies found that the ability of the student representation is the key to success in understanding mathematical concepts and problem solving.
The process of building a relational understanding can be perceived by connecting the mathematical concepts to the representation of images, symbols or words. Skemp (1976) describes relational understanding "knowing both what to do and why". It can be interpreted that relational understanding is the understanding of the students to find out the procedures to be used and has the reason and be able to associate between mathematical concepts. According to Woodruff (2005) that to understanding seen as a phenomenon arising from the interaction of a relational perspective. Forms of understanding as it is called relational understanding type. Besides, Van de Walle et al. (2014) describe the relational understanding means that any concept or a new procedure not only learned, but also connect with the ideas that have been held in order to obtain connections rich ideas. While in one of the goals of mathematics courses in Indonesia in BSNP (2006: 148) states that learners should possess the ability to understand a mathematical concept, explain the link between concepts and apply concepts or algorithms, are flexible, accurate, efficient, and precise, in the breakdown problem.
Learning mathematics towards achieving the relational understanding generating meaningful learning for students. The main purpose of teaching is to reach an understanding which help students todevelop a relational understanding of mathematical ideas. Due to the development of relational understanding is infinite and more complex as someone making connections between ideas, understanding of this type requires a longer time and must have a purpose in every teaching (Van de Walle et al. 2014:5). While based on insights from developmental psychology, understanding of relational roles for children in learning mathematical next(Langhorst and Fritz, 2012; Krajewski and Schneider, 2009; Resnick,1983) in Tubach and Nührenbörger (2014). Thus, relational understanding is one of the objects that are very important in learning mathematics. The studies related to relational understanding have been conducted by: Sahin et al. (2014), Keene et al. (2011), Beswick (2005) and Weber (2002). This article highlights the problems of mathematical representation which are done by students in building a relational understanding through mathematical problem solving. The study related to the measurement of the material is still very limited. The study of the measurement is important in mathematics curriculum from kindergarten through high school because of the usefulness and application of measurement covering aspects very much in our daily lives (NCTM, 2000). The ideas related to the concept of area and perimeter of a rectangle is presented in Figure 1.
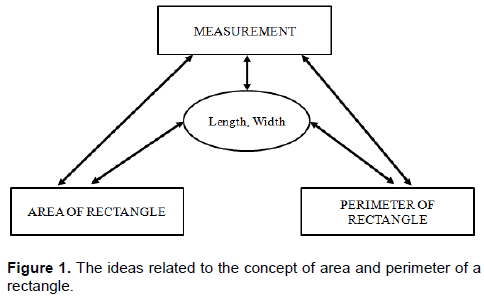
This research uses a case study design. According to Creswell (2009) "is a strategy case studies that explore in depth investigation of the program, activities, processes, one or more individuals". Cases in this study are related to the phenomenon of a mathematical representation of students in building a relational understanding in resolving issues raised in the matter of measurement. Subjects in this study were students in grade 7 were selected on the basis of considerations have spoken and written communication skills are good. To obtain a mathematical representation, individual subjects were asked to solve the problem as outlined on the worksheet. The problem is solved by the subject is "known area of a rectangle is 32 cm2. Pictures and specify rectangular perimeter equal to the perimeter of the rectangle". After completing the subject matter were interviewed to explore linkages between concepts based on the results of his work. The study involved two subjects were selected based on the characterization of mathematical representations that appear. Characterization of mathematical representations that appear is the visual representation embodied in the form of pictures and symbols embodied representation formula for the area and perimeter of a rectangle.
The results of this study report the results of the work of students in solving mathematical problems in measuring material. The results of the student's work are charac-terized in order to obtain two things: the visual representation embodied in the form of images and symbolic representations are realized formula for the area and perimeter of a rectangle.
The visual representation
The visual representation embodied subject 1 (S1) to draw a few rectangles. The rectangular image obtained after the subject to understand the meaning of the problems presented in the form of a sentence. The problem solving process of the subject is figured out from the students’ drawing of a few rectangles, determine the square footage that corresponds to problem solving, determining perimeter (solution of problems), determine the size of the rectangular perimeter equal to the perimeter size of the rectangle on the problem solution. Visual representation of S1 in solving the problem is presented in Figure 2.
The symbolic representation
Symbolic representation embodied subject 2 (S2) by writing a formula for the area and perimeter of a rectangle. Formula area and perimeter of rectangles appear after the subject understand the significance of the problem. The process of resolving the problem of the subject is to write the formula area of a rectangle and determine the value of the length and width, based on the length and width of a predetermined subject entering into the formula around the rectangle to obtain the perimeter of a rectangle (solution of problems), then the subject determine the size rectangles perimeter the same length with rectangle size on the problem solution. S2 mathematical representations to solve problems are presented in Figures 3 and 4.
The results of this study associate with a framework of relational understanding research done by Keene et al. (2011), in his research that there are six stages of relational understanding, namely; 1) Students can guess the results of using the procedure without having to actually do it and they can expect the relationship of the results expected on the results of other procedures. 2) Students can identify with the right to use a specific procedure. 3) Students can correctly use the whole procedure or the selected step in the procedure. Students understand the reason why all the procedures involved. 4) Students understand the reasons why the procedure works as a whole. 5) Students can symbolically or graphics verify the correctness of the result which is claimed as the procedure without repeating the procedure. 6) Students can make connections and is represented in the form of numerical, graphical and symbolic. Furthermore, Keene explained that if students have developed their understanding on the procedures they already have relational understanding. Description of these results are outlined in Table 1.
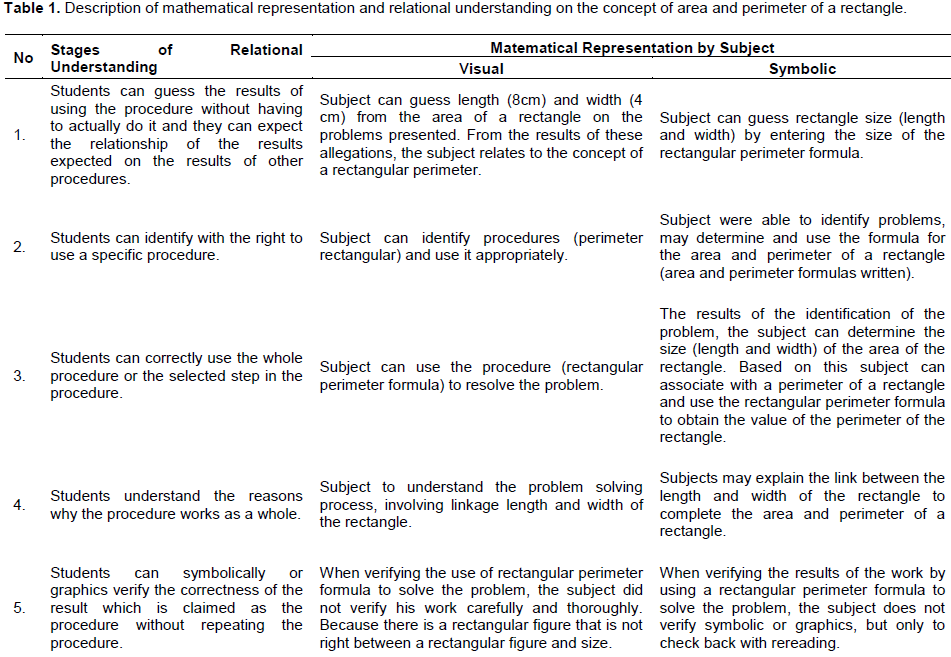

With reference framework developed by the relational understanding Keene et al. (2011), subjects with a visual representation (S1) do not have a relational under-standing of the concept of area and perimeter of a rectangle. It is based on interviews that subjects with a visual representation has not been able to provide an explanation or reasons to use formula for the area and perimeter of a rectangle. Besides it, there is something unique that is found in S1 in providing a visual representation. In resolving the problem S1 draw 10 rectangles are almost the same. Then S1 determines the length and width of the rectangle in order to obtain a rectangular circumference of 24 cm. In giving the size (length and width), S1 did not notice a rectangular shape in order to obtain a rectangular image that is almost the same with different sizes even rectangle size (6 cm long, 6 cm wide) picture is almost the same with the other rectangle shape (Figure 5). Further, the researcher uncovered it through the interview as follows:

Q: Does the size you give on rectangular images have been appropriate?
S1: It is.
Q: Let's see a rectangular image (8 and 4 cm) and (10 and 2 cm). Is the same length 8 cm by 10 cm? Is the same 4 cm long by 2 cm ?.
S1: Emmm different ...
Q: Why is the picture almost the same? Take a look at the rectangle (6cm and 6cm) is a different size?
S1: Earlier I was engrossed in drawing a rectangle, I think that figure does not matter.
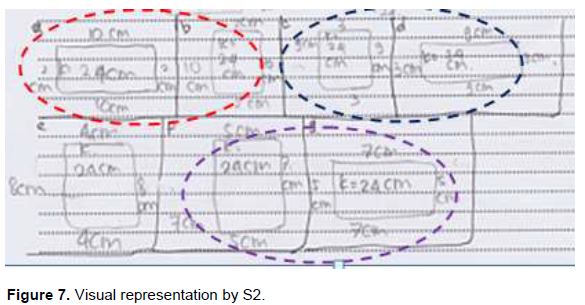
The results of the interview above shows that the visual representation embodied by S1 or rectangular in shape and size, is inaccurate. S1 only using a visual representation as a tool to make it easier to determine the perimeter of the rectangle.These results supported the research Boonen, et al. (2014) found in the schematic representation that there are inaccurate visual mistakes in drawing or in which some parts are missing. The subject to the symbolic representation (S2) has a relational understanding to the concept of area and perimeter of a rectangle. The S2 is able to determine the procedure or formula for the area and perimeter of a rectangle that is obtained when identifying problems. Formula area and perimeter of a rectangle are represented symbolically (written). With a symbolic representation of S2, it determines the length and width of the rectangle to solve problems (Figure 6). Additionally, the symbolic representation, in solving the problems S2 also has a visual representation. This is shown by drawing a rectangle with the same size but with different positions (Figure 7). Results of visual representation by S2 indicates that the S2 attention to the concept of measuring the length and width of the rectangle to the right. S2 uses a visual representation and the size of the rectangle to help determine the circumference of the rectangle. The visual representation shows that S2 is quite accurate.

The results obtained in this study indicate that the subject of representation used in building relational understanding on the concept of area and perimeter of a rectangle is a visual and symbolic representation. Subjects with visual and symbolic representation can build relational under-standing. Although, the visual representation displayed by the subject on the concept of measurement is inaccurate. The visual representation is inaccurate by reason of any error committed in making the subject representations. If this is ignored indeed affects the problem-solving skills and relational understanding students' mastery. This is a problem that needs to be studied by other researchers on the next studies, because the mathematical representation is the key to success in understanding mathematical concepts and problem solving.
The authors have not declared any conflict of interest.
REFERENCES
|
Badan Standar Nasional Pendidikan (BSNP). (2006). Standar Kompetensi dan Kompetensi Dasar SD/MI. Jakarta.
|
|
|
|
Bal AP (2014). The Examination of Representations Used by Classroom Teacher Candidates in Solving Mathematical Problems. Educational Sciences: Theory & Practice. DOI: 10.12738/estp.2014.6.2189.
Crossref
|
|
|
|
|
Beswick K (2005). Preservice Teachers' Understandings of Relational and Instrumental Understanding. Proceeding PME 29.
|
|
|
|
|
Boonen JHA, Wesel FV, JollesJ, Van Der Schoot M (2014). The role of visual representation type, spatial ability, and reading comprehension in word problem solving: An item-level analysis in elementary school children. International Journal of Educational Research.
|
|
|
|
|
Creswell JW (2009). Research design: Qualitative, quantitative, and mixed methods approach. Thousand Oaks, CA: Sage.
|
|
|
|
|
Dündar S (2015). Mathematics Teacher-Candidates Performance in Solving Problem with Different Representation Style: The Trigonometry Example. Eurasia J. Math. Sci. Technol. Educ. 11(6):1379-1397.
|
|
|
|
|
Goldin GA (2002). Representational systems, learning, and problem solving in mathematics. J. Math. Behav. 17(2):137-165.
Crossref
|
|
|
|
|
Keene KA, Glass M, Kim JH (2011). Identifying and Assessing Relational Understanding in Ordinary Differential Equations. Proceeding Frontiers in Education Conference (FIE), 12-15 Oct. 2011.
|
|
|
|
|
NCTM (2000). Principles and Standars for School Mathematics. United States of America: The National Council of Teachers of Mathematics, Inc.
|
|
|
|
|
Sahin Z, Yenmez AA, Erbas AK (2014). Relational Understanding of the Derivative Concept through Mathematical Modeling: A Case Study. Eurasia J. Math. Sci. Technol. Educ. 11(1):177-188.
View
|
|
|
|
|
Skemp R (1976). Relational Understanding and Instrumental Understanding. Mathematics Teaching, The Education Resources Information CenterERIC, (Online) 77:20-26.
|
|
|
|
|
Stylianou DA (2010). Teachers' conceptions of representation in middle school mathematics. J. Mathe. Teacher Educ. 13:325-343. DOI: 10.1007/ s10857-010-9143.
|
|
|
|
|
Tripathi PN (2008). Developing mathematical understanding through multiple representations. Math. Teach. Middle School 13(89):438-445.
|
|
|
|
|
Tubach D, Nührenbörger M (2014). Mathematical Understanding in Transition From Kindergarten to Primary School: Play as Bridge Between Two Educational Institutions.
|
|
|
|
|
Van de Walle JA, Bay-Williams JM, Lovin LAH, Karp KS (2014). Teaching Student-Centered Mathematics: Developmentally Appropriate Instruction for Grades 6-8 (Volume III), 2nd Edition. Boston: Pearson.
|
|
|
|
|
Villegas JL, Castro E, Gutierrez J (2009). Representation in problem solving: A case study with optimization problems. Electronic J. Res. Educ. Psychol. 7(1):279-308.
|
|
|
|
|
Weber K (2002). The role of Instrumental and Relational Understanding in Proofs About Group Isomorphisms. Proceedings from the 2nd International Conference for the Teaching of Mathematics.
|
|
|
|
|
Woodruff E (2005). Manifold Relational Understanding: Moving beyond the mind-as-container metaphor in Educational Technology.
|
|